Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T14:16:58.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle radial velocity and concentration kernels estimation in isotropic grid turbulence experiments of inertialess particles at small separation distances

Published online by Cambridge University Press:  25 May 2022

Si Chen ,
Pierre-Yves Passaggia Open the ORCID record for Pierre-Yves Passaggia [Opens in a new window]  and
Brian L. White Open the ORCID record for Brian L. White [Opens in a new window]
Si Chen
Affiliation:
Earth, Marine, and Environmental Sciences Department, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
Pierre-Yves Passaggia*
Affiliation:
Earth, Marine, and Environmental Sciences Department, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA University of Orléans, INSA-CVL, PRISME, EA 4229, 45072 Orléans, France Carolina Center for Interdisciplinary Applied Mathematics, Department of Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
Brian L. White*
Affiliation:
Earth, Marine, and Environmental Sciences Department, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

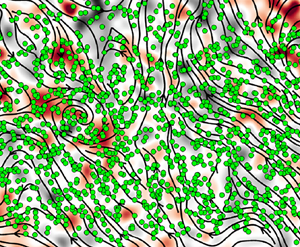
We report experimental measurements of kinematic and dynamic particle concentration kernels conditioned by the separation distances of solid inertialess particles in isotropic turbulence by three-dimensional particle tracking velocimetry with particle diameters smaller than the Kolmogorov length scale. Particle radial relative velocity statistics are measured from the dissipation to the integral length-scale range. The radial scaling of particle and fluid relative velocity variance $\langle w_r(r)^{2} \rangle \sim r^{2/3}$ in the inertial subrange, consistent with Kolmogorov's theory, is reported, while a new scaling is found for small distances due to finite-size effects between particles. The measured concentration kernels at small separation distances therefore deviate from those in the theory of Saffman & Turner (J. Fluid Mech., vol. 1, 1956, pp. 16–30) at small inter-particle distances due to hydrodynamic interactions. A real kernel taking into account the history of the particle tracks and excluding multiple events is also calculated, while the normalised particle concentration kernels are found to be essentially insensitive to the flow Reynolds number.

JFM classification

Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A39
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ababaei, A., Rosa, B., Pozorski, J. & Wang, L.-P. 2021 On the effect of lubrication forces on the collision statistics of cloud droplets in homogeneous isotropic turbulence. J. Fluid Mech. 918, A22.CrossRefGoogle Scholar
Abrahamson, J. 1975 Collision rates of small particles in a vigorously turbulent fluid. Chem. Engng Sci. 30 (11), 1371–1379.CrossRefGoogle Scholar
Akutina, Y. 2016 Experimental investigation of flow structures in a shallow embayment using 3D-PTV. PhD thesis, Karlsruhe Institute of Technology.CrossRefGoogle Scholar
Balachandar, S. 1988 Particle coagulation in homogeneous turbulence. PhD thesis, Brown University.Google Scholar
Barber, C.B., Dobkin, D.P., Dobkin, D.P. & Huhdanpaa, H. 1996 The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 22 (4), 469–483.CrossRefGoogle Scholar
Bewley, G.P., Saw, E.-W. & Bodenschatz, E. 2013 Observation of the sling effect. New J. Phys. 15 (8), 083051.CrossRefGoogle Scholar
Bragg, A.D. & Collins, L.R. 2014 a New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16 (5), 055013.CrossRefGoogle Scholar
Bragg, A.D. & Collins, L.R. 2014 b New insights from comparing statistical theories for inertial particles in turbulence: II. Relative velocities. New J.Phys. 16 (5), 055014.CrossRefGoogle Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.CrossRefGoogle Scholar
Brunk, B.K., Koch, D.L. & Lion, L.W. 1998 a Observations of coagulation in isotropic turbulence. J. Fluid Mech. 371, 81–107.CrossRefGoogle Scholar
Brunk, B.K., Koch, D.L. & Lion, L.W. 1998 b Turbulent coagulation of colloidal particles. J. Fluid Mech. 364, 81–113.CrossRefGoogle Scholar
Cao, L., Pan, G., de Jong, J., Woodward, S. & Meng, H. 2008 Hybrid digital holographic imaging system for three-dimensional dense particle field measurement. Appl. Opt. 47 (25), 4501–4508.CrossRefGoogle ScholarPubMed
Carneiro, M.V., Araújo, N.A.M., Pähtz, T. & Herrmann, H.J. 2013 Midair collisions enhance saltation. Phys. Rev. Lett. 111, 058001.CrossRefGoogle ScholarPubMed
Chen, S. 2020 Particle collision in grid turbulence. PhD thesis, The University of North Carolina at Chapel Hill.Google Scholar
Cox, R.G. & Brenner, H. 1967 The slow motion of a sphere through a viscous fluid towards a plane surface—II small gap widths, including inertial effects. Chem. Engng Sci. 22 (12), 1753–1777.CrossRefGoogle Scholar
Delichatsios, M.A. & Probstein, R.F. 1975 Coagulation in turbulent flow: theory and experiment. J. Colloid Interface Sci. 51 (3), 394–405.CrossRefGoogle Scholar
Dou, Z., Bragg, A.D., Hammond, A.L., Liang, Z., Collins, L.R. & Meng, H. 2018 a Effects of Reynolds number and stokes number on particle-pair relative velocity in isotropic turbulence: a systematic experimental study. J. Fluid Mech. 839, 271–292.CrossRefGoogle Scholar
Dou, Z., Ireland, P.J., Bragg, A.D., Liang, Z., Collins, L.R. & Meng, H. 2018 b Particle-pair relative velocity measurement in high-reynolds-number homogeneous and isotropic turbulence using 4-frame particle tracking velocimetry. Exp. Fluids 59 (2), 30.CrossRefGoogle Scholar
Flagan, R.C. & Seinfeld, J.H. 1988 Fundamentals of Air Pollution Engineering. Prentice-Hall, Inc., Dover.Google Scholar
Grabowski, W.W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45 (1), 293–324.CrossRefGoogle Scholar
Gustavsson, K. & Mehlig, B. 2011 Distribution of relative velocities in turbulent aerosols. Phys. Rev. E 84, 045304.CrossRefGoogle ScholarPubMed
Hammond, A. & Meng, H. 2021 Particle radial distribution function and relative velocity measurement in turbulence at small particle-pair separations. J. Fluid Mech. 921, A16.CrossRefGoogle Scholar
Hill, P.S., Nowell, A.R.M. & Jumars, P.A. 1992 Encounter rate by turbulent shear of particles similar in diameter to the Kolmogorov scale. J. Mar. Res. 50 (4), 643–668.CrossRefGoogle Scholar
Holtzer, G.L. & Collins, L.R. 2002 Relationship between the intrinsic radial distribution function for an isotropic field of particles and lower-dimensional measurements. J. Fluid Mech. 459, 93–102.CrossRefGoogle Scholar
Hwang, W. & Eaton, J.K. 2004 Creating homogeneous and isotropic turbulence without a mean flow. Exp. Fluids 36, 444–454.CrossRefGoogle Scholar
Ireland, P.J., Bragg, A.D. & Collins, L.R. 2016 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.CrossRefGoogle Scholar
Izard, E., Bonometti, T. & Lacaze, L. 2014 Modelling the dynamics of a sphere approaching and bouncing on a wall in a viscous fluid. J. Fluid Mech. 747, 422–446.CrossRefGoogle Scholar
de Jong, J., Salazar, J.P.L.C., Woodward, S.H., Collins, L.R. & Meng, H. 2010 Measurement of inertial particle clustering and relative velocity statistics in isotropic turbulence using holographic imaging. Intl J. Multiphase Flow 36 (4), 324–332.CrossRefGoogle Scholar
Kim, J. & Antonia, R.A. 1993 Isotropy of the small scales of turbulence at low Reynolds number. J. Fluid Mech. 251, 219–238.CrossRefGoogle Scholar
Kiørboe, T., Andersen, K.P. & Dam, H.G. 1990 Coagulation efficiency and aggregate formation in marine phytoplankton. Mar. Biol. 107 (2), 235–245.CrossRefGoogle Scholar
Lüthi, B., Tsinober, A. & Kinzelbach, W. 2005 Lagrangian measurement of vorticity dynamics in turbulent flow. J. Fluid Mech. 528, 87–118.CrossRefGoogle Scholar
Maas, H.G., Gruen, A. & Papantoniou, D. 1993 Particle tracking velocimetry in three-dimensional flows. Exp. Fluids 15 (2), 133–146.CrossRefGoogle Scholar
Marshall, J.S. 2011 Viscous damping force during head-on collision of two spherical particles. Phys. Fluids 23 (1), 013305.CrossRefGoogle Scholar
Maxey, M.R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
McQuarrie, D.A. 1976 Statistical Mechanics. Harper & Row.Google Scholar
Meng, H., Pan, G., Pu, Y. & Woodward, S.H. 2004 Holographic particle image velocimetry: from film to digital recording. Meas. Sci. Technol. 15 (4), 673–685.CrossRefGoogle Scholar
Meunier, P. & Leweke, T. 2003 Analysis and treatment of errors due to high velocity gradients in particle image velocimetry. Exp. Fluids 35 (5), 408–421.CrossRefGoogle Scholar
Meyer, C.J. & Deglon, D.A. 2011 Particle collision modeling – a review. Miner. Engng 24 (8), 719–730.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a voronoï analysis. Phys. Fluids 22 (10), 103304.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.CrossRefGoogle Scholar
Mongruel, A., Lamriben, C., Yahiaoui, S. & Feuillebois, F. 2010 The approach of a sphere to a wall at finite Reynolds number. J. Fluid Mech. 661, 229–238.CrossRefGoogle Scholar
Pan, L. & Padoan, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73–107.CrossRefGoogle Scholar
Pan, L. & Padoan, P. 2014 Turbulence-induced relative velocity of dust particles. IV. The collision kernel. Astrophys. J. 797 (2), 101.CrossRefGoogle Scholar
Passaggia, P.-Y., Chalamalla, V.K., Hurley, M.W., Scotti, A. & Santilli, E. 2020 Estimating pressure and internal-wave flux from laboratory experiments in focusing internal waves. Exp. Fluids 61 (11), 238.CrossRefGoogle Scholar
Passaggia, P.-Y., Leweke, T. & Ehrenstein, U. 2012 Transverse instability and low-frequency flapping in incompressible separated boundary-layer flows: an experimental study. J. Fluid Mech. 703, 363–373.CrossRefGoogle Scholar
Peterson, A.J., Baker, L. & Coletti, F. 2019 Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 864, 925–970.CrossRefGoogle Scholar
Rosa, B., Parishani, H., Ayala, O., Grabowski, W.W. & Wang, L.-P. 2013 Kinematic and dynamic collision statistics of cloud droplets from high-resolution simulations. New J. Phys. 15 (4), 045032.CrossRefGoogle Scholar
Saffman, P.G. & Turner, J.S. 1956 On the collision of drops in turbulent clouds. J. Fluid Mech. 1 (1), 16–30.CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics, vol. 10. Springer.CrossRefGoogle Scholar
Saw, E.-W., Bewley, G.P., Bodenschatz, E., Ray, S.S. & Bec, J. 2014 Extreme fluctuations of the relative velocities between droplets in turbulent airflow. Phys. Fluids 26 (11), 111702.CrossRefGoogle Scholar
Squires, K.D. & Eaton, J.K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids 3 (5), 1169–1178.CrossRefGoogle Scholar
Sundaram, S. & Collins, L.R. 1996 Numerical considerations in simulating a turbulent suspension of finite-volume particles. J. Comput. Phys. 124 (2), 337–350.CrossRefGoogle Scholar
Sundaram, S. & Collins, L.R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Tavoularis, S., Bennett, J.C. & Corrsin, S. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88 (1), 63–69.CrossRefGoogle Scholar
Ten Cate, A., Derksen, J.J., Portela, L.M. & Van Den Akker, H.E.A. 2004 Fully resolved simulations of colliding monodisperse spheres in forced isotropic turbulence. J. Fluid Mech. 519, 233–271.CrossRefGoogle Scholar
Vassilicos, J.C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.CrossRefGoogle Scholar
Voßkuhle, M., Pumir, A. & Lévêque, E. 2011 Estimating the collision rate of inertial particles in a turbulent flow: limitations of the ‘ghost collision’ approximation. J. Phys.: Conf. Ser. 318 (5), 052024.Google Scholar
Wang, L.-P., Franklin, C.N., Ayala, O. & Grabowski, W.W. 2006 Probability distributions of angle of approach and relative velocity for colliding droplets in a turbulent flow. J. Atmos. Sci. 63 (3), 881–900.CrossRefGoogle Scholar
Wang, L.-P., Wexler, A.S. & Zhou, Y. 1998 On the collision rate of small particles in isotropic turbulence. I. Zero-inertia case. Phys. Fluids 10 (1), 266–276.CrossRefGoogle Scholar
Wang, L.-P., Wexler, A.S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.CrossRefGoogle Scholar
Willneff, J. 2003 A spatio-temporal matching algorithm for 3D particle tracking velocimetry. PhD thesis, ETH Zurich.Google Scholar
Xiong, Y. & Pratsinis, S.E. 1991 Gas phase production of particles in reactive turbulent flows. J. Aerosp. Sci. 22 (5), 637–655.CrossRefGoogle Scholar
Yang, F.-L. & Hunt, M.L. 2006 Dynamics of particle–particle collisions in a viscous liquid. Phys. Fluids 18 (12), 121506.CrossRefGoogle Scholar
Zaichik, L.I. & Alipchenkov, V.M. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11 (10), 103018.CrossRefGoogle Scholar