Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-20T06:41:12.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Pair-sphere trajectories in finite-Reynolds-number shear flow

Published online by Cambridge University Press:  17 January 2008

PANDURANG M. KULKARNI  and
JEFFREY F. MORRIS
PANDURANG M. KULKARNI
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
JEFFREY F. MORRIS
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

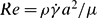The pair trajectories of neutrally buoyant rigid spheres immersed in finite-inertia simple-shear flow are described. The trajectories are obtained using the lattice-Boltzmann method to solve the fluid motion, with Newtonian dynamics describing the sphere motions. The inertia is characterized by the shear-flow Reynolds number , where μ and ρ are the viscosity and density of the fluid respectively, 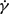is the shear rate and a is the radius of the larger of the pair of spheres in the case of unequal sizes; the majority of results presented are for pairs of equal radii. Reynolds numbers of 0 ≤ Re ≤ 1 are considered with a focus on inertia at Re = O(0.1). At finite inertia, the topology of the pair trajectories is altered from that predicted at Re = 0, as closed trajectories found in Stokes flow vanish and two new forms of trajectories are observed. These include spiralling and reversing trajectories in addition to largely undisturbed open trajectories. For Re = O(0.1), the limits of the various regions in pair space yielding open, reversing and spiralling trajectories are roughly defined.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 596 , 25 January 2008 , pp. 413 - 435
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K., Lu, Y. & Ding, E. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
Batchelor, G. K. 1977 The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 83, 97–117.CrossRefGoogle Scholar
Batchelor, G. K. & Green, J. T. 1972 The hydrodynamic interation of two small freely-moving spheres in a linear flow field. J. Fluid. Mech. 56, 375–400.CrossRefGoogle Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian Dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid. Mech. 348, 103–139.CrossRefGoogle Scholar
Brenner, H. & O'Neill, M. E. 1972 On the Stokes resistance of multiparticle systems in a linear shear field. Chem. Engng Sci. 27, 1421.CrossRefGoogle Scholar
Chun, B. & Ladd, A. J. C. 2006 Inertial migration of neutrally buoyant particles in a square duct: An investigation of multiple equilibrium positions. Phys. Fluids 18, 031704.CrossRefGoogle Scholar
da Cunha, F. R. & Hinch, E. J. 1996 Shear–induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.CrossRefGoogle Scholar
Darabaner, C. L. & Mason, S. G. 1967 Particle motions in sheared suspensions XXII: Interaction of rigid spheres (Experimental). Rheol. Acta. 6, 273–284.CrossRefGoogle Scholar
Ding, E. & Aidun, C. K. 2000 The dynamics and scaling law for particles suspended in shear flow with inertia. J. Fluid Mech. 423, 317–344.CrossRefGoogle Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 277, 271–301.CrossRefGoogle Scholar
Frisch, U., D'Humièrs, D., Hasslacher, B., Lallemand, P., Pomeau, Y. & Rivet, J. P. 1987 Lattice gas hydrodynamics in two and three dimension. Complex Systems 1, 649.Google Scholar
Higuera, F., Succi, S. & Benzi, R. 1989 Lattice gas dynamics with enhanced collisions. Europhys. Lett. 9, 345–349.Google Scholar
Hu, H. H. 1996 Direct simulation of flows of solid-liquid mixtures. Intl J. Multiphase Flow 22, 335–352.CrossRefGoogle Scholar
Hu, H. H., Joseph, D. D. & Crochet, M. J. 1992 Direct simulation of fluid particle motions. Theor. Comput. Fluid Dyn. 3, 285–306.CrossRefGoogle Scholar
Hu, H. H., Patankar, N. A. & Zhu, M. Y. 2001 Direct numerical simulations of fluid-solid systems using the arbitrary Lagrangian-Eulerian technique. J. Comput. Phys 169, 427–462.CrossRefGoogle Scholar
Huang, P. Y. & Joseph, D. D. 2000 Effects of shear thinning on migration of neutrally-buoyant particles in pressure driven flow of Newtonian and viscoelastic fluid. J. Non-Newtonian Fluid Mech. 90, 159–185.CrossRefGoogle Scholar
Jeffrey, D. J. 1992 The calculation of the low Reynolds number resistance functions for two unequal spheres. Phys. Fluids A 4, 16–29.CrossRefGoogle Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid. Mech. 139, 261–290.Google Scholar
Kim, S. & Mifflin, R. T. 1985 The resistance and mobility functions of two equal spheres in low-Reynolds-number flow. Phys. Fluids 28, 2033–2045.CrossRefGoogle Scholar
Koch, D. L. & Hill, R. J. 2001 Inertial effects in suspension and porous media flows. Annu. Rev. Fluid Mech. 33, 619–647.CrossRefGoogle Scholar
Kossack, C. & Acrivos, A. 1974 Steady simple shear flow past a cirular cylinder at moderate Reynolds number: a numerical solution. J. Fluid Mech. 66, 353–376.CrossRefGoogle Scholar
Kromkamp, J., van den Ende, D. T. M., Kandhai, D., van der Sman, R. G. M. & Boom, R. M. 2005 Shear-induced self-diffusion and microstructure in non-Brownian suspensions at non-zero Reynolds number. J. Fluid Mech. 529, 253–278.CrossRefGoogle Scholar
Ladd, A. J. C. 1988 Hydrodynamic interactions in a suspension of spherical particles. J. Chem. Phys. 88, 5051–5063.CrossRefGoogle Scholar
Ladd, A. J. C. 1994 a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
Ladd, A. J. C. 1994 b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.CrossRefGoogle Scholar
Ladd, A. J. C. & Verberg, R. 2001 Lattice-Boltzmann simulations of particle-fluid suspensions. J. Statist. Phys. 104, 1191–1151.CrossRefGoogle Scholar
Leal, L. G. 1992 Laminar Flow and Convective Transport Processes. Butterworth-Heinemann.Google Scholar
Lin, C. J., Lee, K. J. & Sather, N. F. 1970 a Slow motion of two spheres in a shear field. J. Fluid. Mech. 43, 35–47.Google Scholar
Lin, C. J., Peery, J. H. & Schowalter, W. R. 1970 b Simple shear flow round a rigid sphere: Inertial effects and suspension rheology. J. Fluid Mech. 44, 1–17.Google Scholar
Matas, J., Glezer, V., Guazzelli, E. & Morris, J. F. 2004 Trains of particles in finite-Reynolds-number pipe flow. Phys. Fluids 16, 4192–4195.CrossRefGoogle Scholar
Mikulencak, D. R. & Morris, J. F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215–242.CrossRefGoogle Scholar
Nguyen, N. Q. & Ladd, A. J. C. 2002 Lubrication corrections for lattice-Boltzmann simulation of particle suspensions. Phys. Rev. E 66, 046708.Google Scholar
Nirschl, H., Dwyer, H. A. & Denk, V. 1995 Three-dimensional calculations of the simple shear flow around a single particle betwen two moving walls. J. Fluid Mech. 283, 273–285.Google Scholar
Poe, G. G. & Acrivos, A. 1975 Closed streamline flows past rotating single spheres and cylinders: inertia effects. J. Fluid. Mech. 72, 605–623.CrossRefGoogle Scholar
Robertson, C. R. & Acrivos, A. 1970 Low Reynolds number shear flow past a rotating circular cylinder. Part 1. Momentum transfer. J. Fluid Mech. 40, 685–703.Google Scholar
Subramanian, G. & Brady, J. F. 2006 Trajectory analysis for non-Brownian inertial suspensions in simple shear flow. J. Fluid Mech. 559, 151–203.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2006 a Centrifugal forces alter streamline topology and greatly enhance the rate of heat and mass transfer from neutrally buoyant particles to a shear flow. Phys. Rev. Lett 96, 134503.Google Scholar
Subramanian, G. & Koch, D. L. 2006 b Inertial effects on the transfer of heat or mass from neutrally buoyant spheres in a steady linear velocity field. Phys. Fluids 18, 073302.CrossRefGoogle Scholar
Swaminathan, T. N., Mukundakrishnan, K. & Hu, H. H. 2006 Sedimentation of an ellipsoid inside an infinitely long tube at low and intermediate Reynolds numbers. J. Fluid Mech. 551, 357–385.Google Scholar
Wakiya, S., Darabaner, C. L. & Mason, S. G. 1967 Particle motions in sheared suspensions XXI: Interaction of rigid spheres (Theoretical). Rheol. Acta. 6, 273–284.Google Scholar
Zarraga, I. E. & Leighton, D. T. 2001 Normal stress and diffusion in a dilute suspension of hard spheres undergoing simple shear. Phys. Fluids 13, 565–577.Google Scholar
Zettner, C. M. & Yoda, M. 2001 The circular cylinder in simple shear at moderate Reynolds number: An experimental study. Exps. Fluids 30, 346–353.Google Scholar
Zurita-Gotor, M., Bławzdziewicz, J. & Wajnryb, E. 2007 Swapping trajectories: a new cross-streamline particle migration mechanism in a dilute suspension of spheres. J. Fluid Mech. 592, 447–469.Google Scholar