Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T14:22:19.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Outer-layer turbulence intensities in smooth- and rough-wall boundary layers

Published online by Cambridge University Press:  14 June 2013

Ian P. Castro ,
Antonio Segalini  and
P. Henrik Alfredsson
Ian P. Castro*
Affiliation:
Aeronautics, Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Antonio Segalini
Affiliation:
Linné Flow Centre, KTH Stockholm, SE-10044 Stockholm, Sweden
P. Henrik Alfredsson
Affiliation:
Linné Flow Centre, KTH Stockholm, SE-10044 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

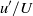Clear differences in turbulence intensity profiles in smooth, transitional and fully rough zero-pressure-gradient boundary layers are demonstrated, using the diagnostic plot introduced by Alfredsson, Segalini & Örlü (Phys. Fluids, vol. 23, 2011, p. 041702) – ${u}^{\prime } / U$ versus 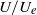$U/ {U}_{e} $, where 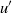${u}^{\prime } $ and 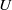$U$ are the local (root mean square) fluctuating and mean velocities and 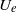${U}_{e} $ is the free stream velocity. A wide range of published data are considered and all zero-pressure-gradient boundary layers yield outer flow 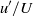${u}^{\prime } / U$ values that are roughly linearly related to 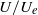$U/ {U}_{e} $, just as for smooth walls, but with a significantly higher slope which is completely independent of the roughness morphology. The difference in slope is due largely to the influence of the roughness parameter (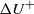$ \mathrm{\Delta} {U}^{+ } $ in the usual notation) and all the data can be fitted empirically by using a modified form of the scaling, dependent only on 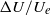$ \mathrm{\Delta} U/ {U}_{e} $. The turbulence intensity, at a location in the outer layer where 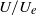$U/ {U}_{e} $ is fixed, rises monotonically with increasing 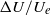$ \mathrm{\Delta} U/ {U}_{e} $ which, however, remains of 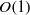$O(1)$ for all possible zero-pressure-gradient rough-wall boundary layers even at the highest Reynolds numbers. A measurement of intensity at a point in the outer region of the boundary layer can provide an indication of whether the surface is aerodynamically fully rough, without having to determine the surface stress or effective roughness height. Discussion of the implication for smooth/rough flow universality of differences in outer-layer mean velocity wake strength is included.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 119 - 131
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H., Örlü, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech B/Fluids 36, 167–175.CrossRefGoogle Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the outer peak. Phys. Fluids 23, 041702.Google Scholar
Amir, M. & Castro, I. P. 2011 Turbulence in rough-wall boundary layers: universality issues. Exp. Fluids 51, 313–326.CrossRefGoogle Scholar
Andreopoulos, J. & Bradshaw, P. 1981 Measurements of turbulence structure in the boundary layer on a rough surface. Boundary-Layer Meteorol. 20, 201–213.CrossRefGoogle Scholar
Antonia, R. A. & Luxton, R. E. 1971 Energy balance in a turbulent boundary layer on a rough wall. Phys. Fluids 14, 1027–1029.Google Scholar
Bergstrom, D. J., Akinlade, O. G. & Tachie, M. F. 2005 Skin friction correlation for smooth and rough wall turbulent boundary layers. Trans. ASME: J. Fluids Engng 127, 1146–1153.Google Scholar
Brzek, B. G., Cal, R. B., Johansson, G. & Castillo, L. 2008 Transitionally rough zero pressure gradient turbulent boundary layers. Exp. Fluids 44, 115–124.CrossRefGoogle Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near-wall flow over urban-type roughness. Boundary-Layer Meteorol. 104, 229–259.Google Scholar
Coles, D. E. 1956 The law of the wake in a turbulent boundary layer. J. Fluid Mech. 1, 191–226.Google Scholar
Cook, N. 1985 Designers Guide to Wind Loading on Building Structures: Part 1. Butterworths.Google Scholar
Fernholz, H. H., Krause, E., Nockerman, M. & Schober, M 1995 Comparative measurements in the canonical boundary layer at $R{e}_{{\delta }_{2} } \lt 60\hspace{0.167em} 000$ on the wall of the German–Dutch wind tunnel. Phys. Fluids 7, 1275–1281.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19, 095104.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17, 035102.Google Scholar
Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50, 233–255.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. G. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Jiménez, J. 2004 Turbulent flow over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Krogstad, P.-Å. & Antonia, R. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27, 450–460.Google Scholar
Krogstad, P.-Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Krogstad, P.-Å. & Efros, V. 2012 About turbulence statistics in the outer part of a boundary layer developing over 2D surface roughness. Phys. Fluids 24, 075112.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Orlandi, P. & Leonardi, S. 2008 Direct numerical simulation of three-dimensional turbulent rough channels: parameterization and flow physics. J. Fluid Mech. 606, 399–415.Google Scholar
Schlichting, H. 1968 Boundary Layer Theory, 6th edn. McGraw-Hill.Google Scholar
Segalini, A., Örlü, R., Castro, I. P. & Alfredsson, P. H. 2012 The streamwise turbulence internsity – a comparison between smooth and rough wall turbulent boundary layers. In Progress in Turbulence V (ed. M. Oberlack, J. Peinke & A. Talamelli), Springer (in press). 5th iTi Conference on Turbulence, Bertinoro, Italy, 30th September–3rd October 2012.Google Scholar
Snyder, W. H. & Castro, I. P. 2002 The critical Reynolds number for rough-wall boundary layers. J. Wind Engng Ind. Aerodyn. 90, 41–54.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2011 Turbulence structure in boundary layers over periodic two- and three-dimensional roughness. J. Fluid Mech. 676, 172–190.Google Scholar