Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T21:47:19.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Outer layer turbulence dynamics in a high-Reynolds-number boundary layer up to 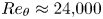$Re_\theta \approx 24{,}000$ recovering from mild separation

Published online by Cambridge University Press:  26 May 2022

Jaime Vaquero Open the ORCID record for Jaime Vaquero [Opens in a new window] ,
Nicolas Renard Open the ORCID record for Nicolas Renard [Opens in a new window]  and
Sébastien Deck Open the ORCID record for Sébastien Deck [Opens in a new window]
Jaime Vaquero
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Nicolas Renard*
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Sébastien Deck
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

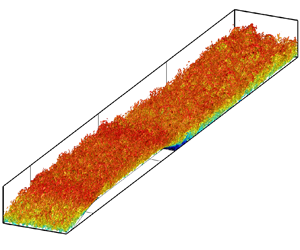
The outer layer dynamics of a high-Reynolds-number boundary layer recovering from non-equilibrium is studied utilising the multi-resolution approach of zonal detached eddy simulation mode 3. The non-equilibrium conditions are obtained from a boundary layer separation over a rounded step enhancing the turbulent production, and recovery happens during redevelopment after reattachment at high Reynolds numbers ($Re_{\theta,max}\approx 24{,}000$). Most of the outer layer turbulence is resolved by the simulation, which reproduces accurately the experimental boundary layer relaxation. The spectral analysis of streamwise velocity fluctuations and turbulent kinetic energy (TKE) production evidences the different turbulent content distribution at separation and within the redevelopment region, at which very large-scale motions are identified with streamwise wavelengths up to $\lambda _x = 9\delta$, where $\delta$ is the boundary layer thickness. The redevelopment of the boundary layer is analysed in terms of the persistence of a secondary peak in the TKE production and the evolution of the wall-shear stress statistics. The skewness and probability density function of the skin friction show a slower relaxation than the downstream flow fraction. This confirms the long-lasting impact of perturbations of the outer layer in high-Reynolds-number wall-bounded flows. This persistent non-equilibrium state is suggested to be the reason for the reported lack of accuracy of the considered Reynolds-averaged Navier–Stokes models in the relaxation region.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A42
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abe, H. 2017 Reynolds-number dependence of wall-pressure fluctuations in a pressure-induced turbulent separation bubble. J. Fluid Mech. 833, 563–598.CrossRefGoogle Scholar
Balakumar, B.J. & Adrian, R.J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365, 665–681.CrossRefGoogle ScholarPubMed
Bentaleb, Y., Lardeau, S. & Leschziner, M.A. 2012 Large-eddy simulation of turbulent boundary layer separation from a rounded step. J. Turbul. 13, N4.CrossRefGoogle Scholar
Bobke, A., Vinuesa, R., Örlü, R. & Schlatter, P. 2017 History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 820, 667–692.CrossRefGoogle Scholar
Cambier, L., Heib, Sébastien, Plot, S. 2013 The Onera elsA CFD software: input from research and feedback from industry. Mech. Indust. 14, 159–174.CrossRefGoogle Scholar
Cécora, R.D., Radespiel, R., Eisfeld, B. & Probst, A. 2015 Differential Reynolds-stress modeling for aeronautics. AIAA J. 53 (3), 739–755.CrossRefGoogle Scholar
Choi, H. & Moin, P. 1994 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113, 1–4.CrossRefGoogle Scholar
Clauser, F.H. 1956 The turbulent boundary layer. In Advances in Applied Mechanics, pp. 1–51. Elsevier.CrossRefGoogle Scholar
Coleman, G.N., Rumsey, C.L. & Spalart, P.R. 2018 Numerical study of turbulent separation bubbles with varying pressure gradient and Reynolds number. J. Fluid Mech. 847, 28–70.CrossRefGoogle ScholarPubMed
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.CrossRefGoogle Scholar
Deck, S. 2012 Recent improvements in the zonal detached eddy simulation (ZDES) formulation. Theor. Comput. Fluid Dyn. 26, 523–550.CrossRefGoogle Scholar
Deck, S. & Laraufie, R. 2013 Numerical investigation of the flow dynamics past a three-element aerofoil. J. Fluid Mech. 732, 401–444.CrossRefGoogle Scholar
Deck, S., Renard, N., Laraufie, R. & Sagaut, P. 2014 a Zonal detached eddy simulation (ZDES) of a spatially developing flat plate turbulent boundary layer over the Reynolds number range $3150 \leq Re_{\theta }\leq 14{,}000$. Phys. Fluids 26, 025116.CrossRefGoogle Scholar
Deck, S., Renard, N., Laraufie, R. & Weiss, P.-É 2014 b Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to $Re_\theta =13650$. J. Fluid Mech. 743, 202–248.CrossRefGoogle Scholar
Deck, Sébastien, Weiss, P.-É., Pamiès, M. & Garnier, E. 2011 Zonal detached eddy simulation of a spatially developing flat plate turbulent boundary layer. Comput. Fluids 48, 1–15.CrossRefGoogle Scholar
Deck, S., Weiss, P.-E. & Renard, N. 2018 A rapid and low noise switch from RANS to WMLES on curvilinear grids with compressible flow solvers. J. Comput. Phys. 363, 231–255.CrossRefGoogle Scholar
Driver, D.M., Seegmiller, H.L. & Marvin, J.G. 1987 Time-dependent behavior of a reattaching shear layer. AIAA J. 25 (7), 914–919.CrossRefGoogle Scholar
Eaton, J.K. & Johnston, J.P. 1981 A review of research on subsonic turbulent flow reattachment. AIAA J. 19 (9), 1093–1100.CrossRefGoogle Scholar
Elyasi, M. & Ghaemi, S. 2019 Experimental investigation of coherent structures of a three-dimensional separated turbulent boundary layer. J. Fluid Mech. 859, 1–32.CrossRefGoogle Scholar
Fadla, F., Alizard, F., Keirsbulck, L., Robinet, J.-C., Laval, J.-P., Foucaut, J.-M., Chovet, C. & Lippert, M. 2019 Investigation of the dynamics in separated turbulent flow. Eur. J. Mech. (B/Fluids) 76, 190–204.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.CrossRefGoogle Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.CrossRefGoogle Scholar
Harun, Z., Monty, J.P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.CrossRefGoogle Scholar
Hasan, M.A.Z. 1992 The flow over a backward-facing step under controlled perturbation: laminar separation. J. Fluid Mech. 238, 73–96.CrossRefGoogle Scholar
Huerre, P. & Rossi, M. 1998 Hydrodynamic instabilities in open flows. In Hydrodynamics and Nonlinear Instabilities, pp. 81–294. Cambridge University Press.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S.C.C. & Smits, A.J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.CrossRefGoogle ScholarPubMed
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program 1988. Center for Turbulence Research.Google Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.CrossRefGoogle ScholarPubMed
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23 (6), 061702.CrossRefGoogle Scholar
Jiménez, J. 1999 The physics of wall turbulence. Physica A 263, 252–262.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.CrossRefGoogle Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25, 101302.CrossRefGoogle Scholar
Kitsios, V., Sekimoto, A., Atkinson, C., Sillero, J.A., Borrell, G., Gungor, A.G., Jiménez, J. & Soria, J. 2017 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation. J. Fluid Mech. 829, 392–419.CrossRefGoogle Scholar
Laraufie, R. & Deck, S. 2013 Assessment of Reynolds stresses tensor reconstruction methods for synthetic turbulent inflow conditions. Application to hybrid RANS/LES methods. Intl J. Heat Fluid Flow 42, 68–78.CrossRefGoogle Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2011 A dynamic forcing method for unsteady turbulent inflow conditions. J. Comput. Phys. 230, 8647–8663.CrossRefGoogle Scholar
Lardeau, S. & Leschziner, M.A. 2011 The interaction of round synthetic jets with a turbulent boundary layer separating from a rounded ramp. J. Fluid Mech. 683, 172–211.CrossRefGoogle Scholar
Launder, B.E., Reece, G.J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.CrossRefGoogle Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.CrossRefGoogle Scholar
Lee, J.H. 2017 Large-scale motions in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 810, 323–361.CrossRefGoogle Scholar
Liou, M.-S. 1996 A sequel to AUSM: AUSM$+$. J. Comput. Phys. 129, 364–382.CrossRefGoogle Scholar
Marusic, I., Chauhan, K.A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.CrossRefGoogle Scholar
Marusic, I. & Heuer, W.D.C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.CrossRefGoogle ScholarPubMed
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.CrossRefGoogle Scholar
Mary, I. & Sagaut, P. 2002 Large eddy simulation of flow around an airfoil near stall. AIAA J. 40, 1139–1145.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K.R. 2011 The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.CrossRefGoogle Scholar
Mellor, G.L. & Gibson, D.M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24, 225.CrossRefGoogle Scholar
Menter, F.R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32, 1598–1605.CrossRefGoogle Scholar
Mohammed-Taifour, A., Schwaab, Q., Pioton, J. & Weiss, J. 2015 A new wind tunnel for the study of pressure-induced separating and reattaching flows. Aeronaut. J. 119 (1211), 91–108.CrossRefGoogle Scholar
Mohammed-Taifour, A. & Weiss, J. 2016 Unsteadiness in a large turbulent separation bubble. J. Fluid Mech. 799, 383–412.CrossRefGoogle Scholar
Mohammed-Taifour, A. & Weiss, J. 2021 Periodic forcing of a large turbulent separation bubble. J. Fluid Mech. 915, A24.CrossRefGoogle Scholar
Na, Y. & Moin, P. 1998 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.CrossRefGoogle Scholar
Nikitin, N.V., Nicoud, F., Wasistho, B., Squires, K.D. & Spalart, P.R. 2000 An approach to wall modeling in large-eddy simulations. Phys. Fluids 12 (7), 1629–1632.CrossRefGoogle Scholar
Österlund, J.M. 1999 Experimental studies of zero pressure-gradient turbulent boundary layer flow. PhD thesis, Department of Mechanics, Royal Institute of Technology, Stockholm.Google Scholar
Pamiès, M., Weiss, P.-E., Garnier, E., Deck, S. & Sagaut, P. 2009 Generation of synthetic turbulent inflow data for large eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 21, 045103.CrossRefGoogle Scholar
Piomelli, U. 2008 Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci. 44, 437–446.CrossRefGoogle Scholar
Radhakrishnan, S., Piomelli, U., Keating, A. & Lopes, A.S. 2006 Reynolds-averaged and large-eddy simulations of turbulent non-equilibrium flows. J. Turbul. 7, N63.CrossRefGoogle Scholar
Renard, N. & Deck, S. 2015 a Improvements in zonal detached eddy simulation for wall modeled large eddy simulation. AIAA J. 53, 3499–3504.CrossRefGoogle Scholar
Renard, N. & Deck, S. 2015 b On the scale-dependent turbulent convection velocity in a spatially developing flat plate turbulent boundary layer at Reynolds number $Re_\theta = 13000$. J. Fluid Mech. 775, 105–148.CrossRefGoogle Scholar
Renard, N. & Deck, S. 2015 c Recent improvements in the formulation of mode III of ZDES (zonal detached eddy simulation) for WMLES use at $Re_\theta > 10^4$. In 53rd AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics.CrossRef+10^4$.+In+53rd+AIAA+Aerospace+Sciences+Meeting.+American+Institute+of+Aeronautics+and+Astronautics.>Google Scholar
Renard, N. & Deck, S. 2016 A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech. 790, 339–367.CrossRefGoogle Scholar
Rotta, J.C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2, 1–95.CrossRefGoogle Scholar
Sagaut, P., Deck, S. & Terracol, M. 2013 Multiscale and Multiresolution Approaches in Turbulence, 2nd edn. Imperial College Press.CrossRefGoogle Scholar
Sanmiguel Vila, C., Vinuesa, R., Discetti, S., Ianiro, A., Schlatter, P. & Örlü, R. 2017 On the identification of well-behaved turbulent boundary layers. J. Fluid Mech. 822, 109–138.CrossRefGoogle Scholar
Sanmiguel Vila, C., Vinuesa, R., Discetti, S., Ianiro, A., Schlatter, P. & Örlü, R. 2020 Separating adverse-pressure-gradient and Reynolds-number effects in turbulent boundary layers. Phys. Rev. Fluids 5 (6), 064609.CrossRefGoogle Scholar
Schatzman, D.M. & Thomas, F.O. 2017 An experimental investigation of an unsteady adverse pressure gradient turbulent boundary layer: embedded shear layer scaling. J. Fluid Mech. 815, 592–642.CrossRefGoogle Scholar
Simpson, R.L. 1981 A review of some phenomena in turbulent flow separation. J. Fluids Eng. 103 (4), 520–533.CrossRefGoogle Scholar
Simpson, R.L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21, 205–232.CrossRefGoogle Scholar
Simpson, R.L., Chew, Y. -T. & Shivaprasad, B.G. 1981 The structure of a separating turbulent boundary layer. Part 2. Higher-order turbulence results. J. Fluid Mech. 113, 53–73.CrossRefGoogle Scholar
Smits, A.J. 2020 Some observations on Reynolds number scaling in wall-bounded flows. Phys. Rev. Fluids 5 (11), 110514.CrossRefGoogle Scholar
Smits, A.J., McKeon, B.J. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375. doi:10.1146/annurev-fluid-122109-160753CrossRefGoogle Scholar
Song, S. 2002 Reynolds number effects on a turbulent boundary layer with separation, reattachment and recovery. PhD thesis, Stanford University.Google Scholar
Song, S. & Eaton, J.K. 2004 Reynolds number effects on a turbulent boundary layer with separation, reattachment, and recovery. Exp. Fluids 36, 246–258.CrossRefGoogle Scholar
Spalart, P. & Allmaras, S. 1994 A one-equation turbulence model for aerodynamic flows. La Rech. Aérosp. (1), 5–21.Google Scholar
Spalart, P.R., Jou, W-H., Strelets, M. & Allmaras, S.R. 1997 Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. In Proceedings of the First AFOSR International Conference on DNS/LES, pp. 137–147. Greyden Press.Google Scholar
Spalart, P.R. & Watmuff, J.H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337.CrossRefGoogle Scholar
Speziale, C.G., Sarkar, S. & Gatski, T.B. 1991 Modelling the pressure–strain correlation of turbulence: an invariant dynamical systems approach. J. Fluid Mech. 227, 245–272.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A.J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.CrossRefGoogle Scholar
Vaquero, J., Renard, N. & Deck, S. 2019 a Advanced simulations of turbulent boundary layers under pressure-gradient conditions. Phys. Fluids 31 (11), 115111.CrossRefGoogle Scholar
Vaquero, J., Renard, N. & Deck, S. 2019 b Effects of upstream perturbations on the solution of the laminar and fully turbulent boundary layer equations with pressure gradients. Phys. Fluids 31 (12), 125103.CrossRefGoogle Scholar
Weiss, J., Mohammed-Taifour, A. & Schwaab, Q. 2015 Unsteady behavior of a pressure-induced turbulent separation bubble. AIAA J. 53 (9), 2634–2645.CrossRefGoogle Scholar
Welch, P. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73.CrossRefGoogle Scholar
Wu, W., Meneveau, C. & Mittal, R. 2020 Spatio-temporal dynamics of turbulent separation bubbles. J. Fluid Mech. 883, A45.CrossRefGoogle Scholar