Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T04:04:28.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal sensor and actuator placement for feedback control of vortex shedding

Published online by Cambridge University Press:  02 December 2021

Bo Jin Open the ORCID record for Bo Jin [Opens in a new window] ,
Simon J. Illingworth Open the ORCID record for Simon J. Illingworth [Opens in a new window]  and
Richard D. Sandberg Open the ORCID record for Richard D. Sandberg [Opens in a new window]
Bo Jin*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, VIC3010, Australia
Simon J. Illingworth
Affiliation:
Department of Mechanical Engineering, University of Melbourne, VIC3010, Australia
Richard D. Sandberg
Affiliation:
Department of Mechanical Engineering, University of Melbourne, VIC3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

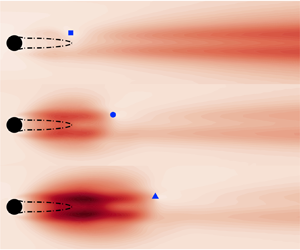
We consider linear feedback control of the two-dimensional flow past a cylinder at low Reynolds numbers, with a particular focus on the optimal placement of a single sensor and a single actuator. To accommodate the high dimensionality of the flow, we compute its leading resolvent forcing and response modes to enable the design of $\mathcal {H}_2$-optimal estimators and controllers. We then investigate three control problems: (i) optimal estimation (OE) in which we measure the flow at a single location and estimate the entire flow; (ii) full-state information control (FIC) in which we measure the entire flow but actuate at only one location; and (iii) the overall feedback control problem in which a single sensor is available for measurement and a single actuator is available for control. We characterize the performance of these control arrangements over a range of sensor and actuator placements and discuss implications for effective feedback control when using a single sensor and a single actuator. The optimal sensor and actuator placements found for the OE and FIC problems are also compared with those found for the overall feedback control problem over a range of Reynolds numbers. This comparison reveals the key factors and conflicting trade-offs that limit feedback control performance.

JFM classification

Flow Control: Control theory Vortex Flows: Vortex shedding Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 932 , 10 February 2022 , A2
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Åkervik, E., Hœpffner, J., Ehrenstein, U.W.E. & Henningson, D.S. 2007 Optimal growth, model reduction and control in a separated boundary-layer flow using global eigenmodes. J. Fluid Mech. 579, 305–314.CrossRefGoogle Scholar
Akhtar, I., Borggaard, J., Burns, J.A., Imtiaz, H. & Zietsman, L. 2015 Using functional gains for effective sensor location in flow control: a reduced-order modelling approach. J. Fluid Mech. 781, 622–656.CrossRefGoogle Scholar
Amestoy, P.R., Duff, I.S., L'Excellent, J.Y. & Koster, J. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Applics. 23 (1), 15–41.CrossRefGoogle Scholar
Bagheri, S., Henningson, D.S., Hoepffner, J. & Schmid, P.J. 2009 Input-output analysis and control design applied to a linear model of spatially developing flows. Appl. Mech. Rev. 62 (2), 020803.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Belson, B.A., Semeraro, O., Rowley, C.W. & Henningson, D.S. 2013 Feedback control of instabilities in the two-dimensional blasius boundary layer: the role of sensors and actuators. Phys. Fluids 25 (5), 054106.CrossRefGoogle Scholar
Benner, P., Köhler, M. & Saak, J. 2019 M.E.S.S.–the matrix equations sparse solvers library. https://www.mpi-magdeburg.mpg.de/projects/mess.Google Scholar
Camarri, S. & Iollo, A. 2010 Feedback control of the vortex-shedding instability based on sensitivity analysis. Phys. Fluids 22 (9), 094102.CrossRefGoogle Scholar
Ceccio, S.L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.CrossRefGoogle Scholar
Chen, K.K. & Rowley, C.W. 2011 $\mathcal {H}_2$ optimal actuator and sensor placement in the linearised complex Ginzburg–Landau system. J. Fluid Mech. 681, 241–260.CrossRefGoogle Scholar
Chen, K.K. & Rowley, C.W. 2014 Fluid flow control applications of $\mathcal {H}_2$ optimal actuator and sensor placement. In 2014 American Control Conference, pp. 4044–4049. IEEE.CrossRefGoogle Scholar
Choi, H., Jeon, W.P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Chomaz, J.M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Chomaz, J.M., Huerre, P. & Redekopp, L.G. 1991 A frequency selection criterion in spatially developing flows. Stud. Appl. Maths 84 (2), 119–144.CrossRefGoogle Scholar
Cohen, K., Siegel, S. & McLaughlin, T. 2006 A heuristic approach to effective sensor placement for modeling of a cylinder wake. Comput. Fluids 35 (1), 103–120.CrossRefGoogle Scholar
Croci, M., Giles, M.B., Rognes, M.E. & Farrell, P.E. 2018 Efficient white noise sampling and coupling for multilevel Monte Carlo with nonnested meshes. SIAM/ASA J. Uncertain. Quantif. 6 (4), 1630–1655.CrossRefGoogle Scholar
Deylami, H.M., Amanifard, N., Hosseininezhad, S.S. & Dolati, F. 2017 Numerical investigation of the wake flow control past a circular cylinder with electrohydrodynamic actuator. Eur. J. Mech. B/Fluids 66, 71–80.CrossRefGoogle Scholar
Doyle, J., Glover, K., Khargonekar, P. & Francis, B. 1988 State-space solutions to standard $\mathcal {H}_2$ and $\mathcal {H}_{\infty }$ control problems. In 1988 American Control Conference, pp. 1691–1696. IEEE.Google Scholar
Gad-el Hak, M. 2007 Flow Control: Passive, Active, and Reactive Flow Management. Cambridge University Press.Google Scholar
Gad-el Hak, M., Pollard, A. & Bonnet, J.P. 2003 Flow Control: Fundamentals and Practices, vol. 53. Springer Science & Business Media.Google Scholar
Georgiou, T.T. & Lindquist, A. 2013 The separation principle in stochastic control, redux. IEEE Trans. Autom. Control 58 (10), 2481–2494.CrossRefGoogle Scholar
Gerhard, J., Pastoor, M., King, R., Noack, B., Dillmann, A., Morzynski, M. & Tadmor, G. 2003 Model-based control of vortex shedding using low-dimensional Galerkin models. In 33rd AIAA Fluid Dynamics Conference and Exhibit, p. 4262.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Hiramoto, K., Doki, H. & Obinata, G. 2000 Optimal sensor/actuator placement for active vibration control using explicit solution of algebraic Riccati equation. J. Sound Vib. 229 (5), 1057–1075.CrossRefGoogle Scholar
Hu, W., Morris, K. & Zhang, Y. 2016 Sensor location in a controlled thermal fluid. In 2016 IEEE 55th Conference on Decision and Control, pp. 2259–2264. IEEE.CrossRefGoogle Scholar
Hwang, Y. & Choi, H. 2006 Control of absolute instability by basic-flow modification in a parallel wake at low Reynolds number. J. Fluid Mech. 560, 465–475.CrossRefGoogle Scholar
Hyun, K.T. & Chun, C.H. 2003 The wake flow control behind a circular cylinder using ion wind. Exp. Fluids 35 (6), 541–552.CrossRefGoogle Scholar
Jin, B., Illingworth, S.J. & Sandberg, R.D. 2020 Feedback control of vortex shedding using a resolvent-based modelling approach. J. Fluid Mech. 897, A26.CrossRefGoogle Scholar
Jin, B., Illingworth, S.J. & Sandberg, R.D. 2021 Resolvent-based approach for H2-optimal estimation and control: an application to the cylinder flow. arXiv:2105.04927.Google Scholar
Juillet, F., Schmid, P.J. & Huerre, P. 2013 Control of amplifier flows using subspace identification techniques. J. Fluid Mech. 725, 522–565.CrossRefGoogle Scholar
Khan, T., Morris, K. & Stastna, M. 2015 Computation of the optimal sensor location for the estimation of an 1-D linear dispersive wave equation. In 2015 American Control Conference, pp. 5270–5275. IEEE.CrossRefGoogle Scholar
Kim, J. & Bewley, T.R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.CrossRefGoogle Scholar
Lauga, E. & Bewley, T.R. 2003 The decay of stabilizability with Reynolds number in a linear model of spatially developing flows. Proc. R. Soc. Lond. A 459 (2036), 2077–2095.CrossRefGoogle Scholar
Lauga, E. & Bewley, T.R. 2004 Performance of a linear robust control strategy on a nonlinear model of spatially developing flows. J. Fluid Mech. 512, 343–374.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods, vol. 6. SIAM.CrossRefGoogle Scholar
Leontini, J.S., Stewart, B.E., Thompson, M.C. & Hourigan, K. 2006 Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18 (6), 067101.CrossRefGoogle Scholar
Lienhard, J.H. 1966 Synopsis of Lift, Drag, and Vortex Frequency Data for Rigid Circular Cylinders, vol. 300. Technical Extension Service, Washington State University.Google Scholar
Logg, A., Mardal, K.A. & Wells, G. 2012 Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book, vol. 84. Springer Science & Business Media.CrossRefGoogle Scholar
Ma, Z., Ahuja, S. & Rowley, C.W. 2011 Reduced-order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 25 (1-4), 233–247.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Monkewitz, P.A., Huerre, P. & Chomaz, J.M. 1993 Global linear stability analysis of weakly non-parallel shear flows. J. Fluid Mech. 251, 1–20.CrossRefGoogle Scholar
Mons, V., Chassaing, J.C. & Sagaut, P. 2017 Optimal sensor placement for variational data assimilation of unsteady flows past a rotationally oscillating cylinder. J. Fluid Mech. 823, 230–277.CrossRefGoogle Scholar
Natarajan, M., Freund, J.B. & Bodony, D.J. 2016 Actuator selection and placement for localized feedback flow control. J. Fluid Mech. 809, 775–792.CrossRefGoogle Scholar
Oehler, S.F. & Illingworth, S.J. 2018 Sensor and actuator placement trade-offs for a linear model of spatially developing flows. J. Fluid Mech. 854, 34–55.CrossRefGoogle Scholar
Paris, R., Beneddine, S. & Dandois, J. 2021 Robust flow control and optimal sensor placement using deep reinforcement learning. J. Fluid Mech. 913, A25.CrossRefGoogle Scholar
Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.CrossRefGoogle Scholar
Ribeiro, J.H.M., Yeh, C.-A. & Taira, K. 2020 Randomized resolvent analysis. Phys. Rev. Fluids 5 (3), 033902.CrossRefGoogle Scholar
Roussopoulos, K. 1993 Feedback control of vortex shedding at low Reynolds numbers. J. Fluid Mech. 248, 267–296.CrossRefGoogle Scholar
Saak, J., Köhler, M. & Benner, P. 2019 M-M.E.S.S.-2.0–the matrix equations sparse solvers library. doi:10.5281/zenodo.3368844, see also: www.mpi-magdeburg.mpg.de/projects/mess.CrossRefGoogle Scholar
Schmid, P.J. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity. Appl. Mech. Rev. 66 (2), 024803.CrossRefGoogle Scholar
Seidel, J., Siegel, S., Fagley, C., Cohen, K. & McLaughlin, T. 2009 Feedback control of a circular cylinder wake. Proc. Inst. Mech. Engrs G 223 (4), 379–392.CrossRefGoogle Scholar
Sipp, D. & Marquet, O. 2013 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27 (5), 617–635.CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 030801.CrossRefGoogle Scholar
Skogestad, S. & Postlethwaite, I. 2007 Multivariable Feedback Control: Analysis and Design, vol. 2. Wiley.Google Scholar
Strykowski, P.J. & Sreenivasan, K.R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
Tan, J., Zhang, D. & Lv, L. 2018 A review on enhanced mixing methods in supersonic mixing layer flows. Acta Astronaut. 152, 310–324.CrossRefGoogle Scholar
Toedtli, S.S., Luhar, M. & McKeon, B.J. 2019 Predicting the response of turbulent channel flow to varying-phase opposition control: resolvent analysis as a tool for flow control design. Phys. Rev. Fluids 4 (7), 073905.CrossRefGoogle Scholar
Tritton, D.J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid. Mech. 6 (4), 547–567.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar