Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-31T02:40:37.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Onset of global instability in low-density jets

Published online by Cambridge University Press:  04 September 2017

Yuanhang Zhu ,
Vikrant Gupta Open the ORCID record for Vikrant Gupta [Opens in a new window]  and
Larry K. B. Li Open the ORCID record for Larry K. B. Li [Opens in a new window]
Yuanhang Zhu
Affiliation:
Department of Mechanical and Aerospace Engineering, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong
Vikrant Gupta
Affiliation:
Department of Mechanical and Aerospace Engineering, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, China
Larry K. B. Li*
Affiliation:
Department of Mechanical and Aerospace Engineering, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

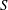In low-density axisymmetric jets, the onset of global instability is known to depend on three control parameters, namely the jet-to-ambient density ratio $S$, the initial momentum thickness 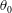$\unicode[STIX]{x1D703}_{0}$ and the Reynolds number 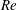$Re$. For sufficiently low values of 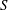$S$ and 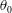$\unicode[STIX]{x1D703}_{0}$, these jets bifurcate from a steady state (a fixed point) to a self-excited oscillatory state (a limit cycle) when 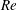$Re$ increases above a critical value corresponding to the Hopf point, 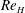$Re_{H}$. In the literature, this Hopf bifurcation is often regarded as supercritical. In this experimental study, however, we find that under some conditions, there exists a hysteretic bistable region at 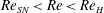$Re_{SN}<Re<Re_{H}$, where 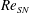$Re_{SN}$ denotes a saddle-node point. This shows that, contrary to expectations, the Hopf bifurcation can also be subcritical, which we explore by evaluating the coefficients of a truncated Landau model. The existence of subcritical bifurcations implies the potential for triggering and the need for weakly nonlinear analyses to be performed to at least fifth order if one is to be able to predict saturation and bistability. We conclude by proposing a universal scaling for 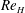$Re_{H}$ in terms of 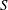$S$ and 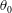$\unicode[STIX]{x1D703}_{0}$. This scaling, which is insensitive to the super/subcritical nature of the bifurcations, can be used to predict the onset of self-excited oscillations, providing further evidence to support Hallberg & Strykowski’s concept (J. Fluid Mech., vol. 569, 2006, pp. 493–507) of universal global modes in low-density jets.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Wakes/Jets: Jets Instability: Nonlinear instability
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1988 Bifurcations to local and global modes in spatially developing flows. Phys. Rev. Lett. 60 (1), 25–28.Google Scholar
Coenen, W., Lesshafft, L., Garnaud, X. & Sevilla, A. 2017 Global instability of low-density jets. J. Fluid Mech. 820, 187–207.Google Scholar
Coenen, W. & Sevilla, A. 2012 The structure of the absolutely unstable regions in the near field of low-density jets. J. Fluid Mech. 713, 123–149.Google Scholar
Coenen, W., Sevilla, A. & Sánchez, A. L. 2008 Absolute instability of light jets emerging from circular injector tubes. Phys. Fluids 20 (7), 074104.Google Scholar
Davitian, J., Getsinger, D., Hendrickson, C. & Karagozian, A. R. 2010 Transition to global instability in transverse-jet shear layers. J. Fluid Mech. 661, 294–315.Google Scholar
Dušek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.Google Scholar
Gopalakrishnan, E. A. & Sujith, R. I. 2015 Effect of external noise on the hysteresis characteristics of a thermoacoustic system. J. Fluid Mech. 776, 334–353.Google Scholar
Hallberg, M. P., Srinivasan, V., Gorse, P. & Strykowski, P. J. 2007 Suppression of global modes in low-density axisymmetric jets using coflow. Phys. Fluids 19 (1), 4102.Google Scholar
Hallberg, M. P. & Strykowski, P. J. 2006 On the universality of global modes in low-density axisymmetric jets. J. Fluid Mech. 569, 493–507.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Jendoubi, S. & Strykowski, P. J. 1994 Absolute and convective instability of axisymmetric jets with external flow. Phys. Fluids 6 (9), 3000–3009.Google Scholar
Kyle, D. M. & Sreenivasan, K. R. 1993 The instability and breakdown of a round variable-density jet. J. Fluid Mech. 249, 619–664.Google Scholar
Lesshafft, L., Huerre, P. & Sagaut, P. 2007 Frequency selection in globally unstable round jets. Phys. Fluids 19 (5), 054108.Google Scholar
Lesshafft, L., Huerre, P., Sagaut, P. & Terracol, M. 2006 Nonlinear global modes in hot jets. J. Fluid Mech. 554, 393–409.Google Scholar
Lesshafft, L. & Marquet, O. 2010 Optimal velocity and density profiles for the onset of absolute instability in jets. J. Fluid Mech. 662, 398–408.Google Scholar
Li, L. K. B. & Juniper, M. P. 2013a Lock-in and quasiperiodicity in a forced hydrodynamically self-excited jet. J. Fluid Mech. 726, 624–655.CrossRefGoogle Scholar
Li, L. K. B. & Juniper, M. P. 2013b Lock-in and quasiperiodicity in hydrodynamically self-excited flames: experiments and modelling. Proc. Combust. Inst. 34, 947–954.Google Scholar
Li, L. K. B. & Juniper, M. P. 2013c Phase trapping and slipping in a forced hydrodynamically self-excited jet. J. Fluid Mech. 735, R5.Google Scholar
Monkewitz, P. A., Bechert, D. W., Barsikow, B. & Lehmann, B. 1990 Self-excited oscillations and mixing in a heated round jet. J. Fluid Mech. 213, 611–639.Google Scholar
Monkewitz, P. A. & Sohn, K. 1988 Absolute instability in hot jets. AIAA J. 26 (8), 911–916.Google Scholar
Nichols, J. W., Schmid, P. J. & Riley, J. J. 2007 Self-sustained oscillations in variable-density round jets. J. Fluid Mech. 582, 341–376.Google Scholar
Pier, B. & Huerre, P. 2001 Nonlinear self-sustained structures and fronts in spatially developing wake flows. J. Fluid Mech. 435, 145–174.Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Raghu, S. & Monkewitz, P. A. 1991 The bifurcation of a hot round jet to limit-cycle oscillations. Phys. Fluids 3 (4), 501–503.CrossRefGoogle Scholar
Raynal, L., Harion, J. L., Favre-Marinet, M. & Binder, G. 1996 The oscillatory instability of plane variable-density jets. Phys. Fluids 8 (4), 993–1006.Google Scholar
Rockwell, D. & Naudascher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11 (1), 67–94.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Sreenivasan, K. R., Raghu, S. & Kyle, D. 1989 Absolute instability in variable density round jets. Exp. Fluids 7 (5), 309–317.Google Scholar
Srinivasan, V., Hallberg, M. P. & Strykowski, P. J. 2010 Viscous linear stability of axisymmetric low-density jets: parameters influencing absolute instability. Phys. Fluids 22 (2), 024103.Google Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. Perseus Books.Google Scholar
Zakharova, A., Vadivasova, T., Anishchenko, V., Koseska, A. & Kurths, J. 2010 Stochastic bifurcations and coherence like resonance in a self-sustained bistable noisy oscillator. Phys. Rev. E 81 (1), 011106.Google Scholar