Hostname: page-component-5cf477f64f-zrtmk Total loading time: 0 Render date: 2025-04-07T22:33:04.841Z Has data issue: false hasContentIssue false
  • English
  • Français

On the wall-bounded model of fingering double diffusive convection

Published online by Cambridge University Press:  20 October 2023

Junyi Li Open the ORCID record for Junyi Li [Opens in a new window]  and
Yantao Yang Open the ORCID record for Yantao Yang [Opens in a new window]
Junyi Li
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, and Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China Joint Laboratory of Marine Hydrodynamics and Ocean Engineering, Laoshan Laboratory, Shandong 266299, PR China
Yantao Yang*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, and Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China Joint Laboratory of Marine Hydrodynamics and Ocean Engineering, Laoshan Laboratory, Shandong 266299, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

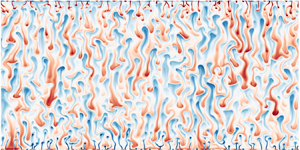
The present work aims at clarifying the effects of a solid boundary on the salt fingers in the wall-bounded double diffusive convection turbulence driven by the salinity and temperature differences between the top and bottom plates. The fluid properties are the same as the seawater, and two-dimensional direct numerical simulations are conducted over a wide range of the thermal and salinity Rayleigh numbers which measure the strength of driving salinity difference and stabilising temperature difference. We find that the bulk density ratio $\varLambda _b$, defined by the mean temperature and salinity gradients at the bulk, controls the flow morphology. As $\varLambda _b$ exceeds unity, the bulk flow shifts from wide convection rolls to slender salt fingers. Two different regimes are further identified for the cases of salt-finger type. One is the confined salt-finger regime where the characteristic height of salt fingers is comparable to the bulk height and the influences of the solid boundary are noticeable. The other is the free salt-finger regime where the salt fingers are much shorter than the bulk height. In this latter regime, the transport properties versus $\varLambda _b$ are in quantitative agreement with those obtained in the fully periodic domain (e.g. Traxler et al., J. Fluid Mech., vol. 677, 2011, pp. 530–553). For a limited range of density ratio at the highest salinity Rayleigh number considered here, multiple states can be obtained from different initial conditions. The large-scale secondary instability and spontaneous formation of staircase from finger layers are not observed in the current study.

JFM classification

Convection: Double diffusive convection Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 973 , 25 October 2023 , A37
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.10.1103/RevModPhys.81.503CrossRefGoogle Scholar
Ashin, K., Girishkumar, M.S., Joseph, J., D'asaro, E., Sureshkumar, N., Sherin, V.R., Murali, B., Thangaprakash, V.P., Rao, E.P.R. & Shenoi, S.S.C. 2022 Double diffusion in the Arabian Sea during winter and spring. J. Phys. Oceanogr. 52 (6), 1205–1231.10.1175/JPO-D-21-0186.1CrossRefGoogle Scholar
Buffett, G.G., Krahmann, G., Klaeschen, D., Schroeder, K., Sallarès, V., Papenberg, C., Ranero, C.R. & Zitellini, N. 2017 Seismic oceanography in the Tyrrhenian Sea: thermohaline staircases, eddies, and internal waves. J. Geophys. Res.: Oceans 122 (11), 8503–8523.10.1002/2017JC012726CrossRefGoogle Scholar
Calzavarini, E., Doering, C.R., Gibbon, J.D., Lohse, D., Tanabe, A. & Toschi, F. 2006 Exponentially growing solutions in homogeneous Rayleigh–Bénard convection. Phys. Rev. E 73, 035301.10.1103/PhysRevE.73.035301CrossRefGoogle ScholarPubMed
Durante, S., Schroeder, K., Mazzei, L., Pierini, S., Borghini, M. & Sparnocchia, S. 2019 Permanent thermohaline staircases in the Tyrrhenian Sea. Geophys. Res. Lett. 46, 1562–1570.10.1029/2018GL081747CrossRefGoogle Scholar
Hage, E. & Tilgner, A. 2010 High Rayleigh number convection with double diffusive fingers. Phys. Fluids 22 (7), 076603.10.1063/1.3464158CrossRefGoogle Scholar
von Hardenberg, J. & Paparella, F. 2010 Non-Gaussian buoyancy statistics in fingering convection. Phys. Lett. A 374 (26), 2646–2653.10.1016/j.physleta.2010.04.051CrossRefGoogle Scholar
Huppert, H.E. & Turner, J.S. 1981 Double-diffusive convection. J. Fluid Mech. 106, 299–329.10.1017/S0022112081001614CrossRefGoogle Scholar
Johnson, G.C. & Kearney, K.A. 2009 Ocean climate change fingerprints attenuated by salt fingering? Geophys. Res. Lett. 36 (21), L21603.CrossRefGoogle Scholar
Kelley, D.E., Fernando, H.J.S., Gargett, A.E., Tanny, J. & Özsoy, E. 2003 The diffusive regime of double-diffusive convection. Prog. Oceanogr. 56 (3–4), 461–481.10.1016/S0079-6611(03)00026-0CrossRefGoogle Scholar
Kellner, M. & Tilgner, A. 2014 Transition to finger convection in double-diffusive convection. Phys. Fluids 26 (9), 094103.10.1063/1.4895844CrossRefGoogle Scholar
Krishnamurti, R. 2003 Double-diffusive transport in laboratory thermohaline staircases. J. Fluid Mech. 483, 287–314.10.1017/S0022112003004166CrossRefGoogle Scholar
Kunze, E. 2003 A review of oceanic salt-fingering theory. Prog. Oceanogr. 56, 399–417.CrossRefGoogle Scholar
Linden, P.F. 1973 On the structure of salt fingers. Deep-Sea Res. 20, 325–340.Google Scholar
Linden, P.F. 1978 The formation of banded salt finger structure. J. Geophys. Res.: Oceans 83 (C6), 2902–2912.10.1029/JC083iC06p02902CrossRefGoogle Scholar
Middleton, L. & Taylor, J.R. 2020 A general criterion for the release of background potential energy through double diffusion. J. Fluid Mech. 893, R3.10.1017/jfm.2020.259CrossRefGoogle Scholar
Ostilla-Mónico, R., Yang, Y., van der Poel, E.P., Lohse, D. & Verzicco, R. 2015 A multiple resolutions strategy for direct numerical simulation of scalar turbulence. J. Comput. Phys. 301, 308–321.10.1016/j.jcp.2015.08.031CrossRefGoogle Scholar
Paparella, F. & von Hardenberg, J. 2012 Clustering of salt fingers in double-diffusive convection leads to staircase like stratification. Phys. Rev. Lett. 109, 014502.10.1103/PhysRevLett.109.014502CrossRefGoogle Scholar
Radko, T. 2003 A mechanism for layer formation in a double-diffusive fluid. J. Fluid Mech. 497, 365–380.10.1017/S0022112003006785CrossRefGoogle Scholar
Radko, T. 2008 The double-diffusive modon. J. Fluid Mech. 609, 59–85.10.1017/S0022112008002127CrossRefGoogle Scholar
Radko, T. 2013 Double-Diffusive Convection. Cambridge University Press.10.1017/CBO9781139034173CrossRefGoogle Scholar
Radko, T. & Stern, M.E. 2000 Finite-amplitude salt fingers in a vertically bounded layer. J. Fluid Mech. 425, 133–160.10.1017/S0022112000002135CrossRefGoogle Scholar
Rosenthal, A., Lüdemann, K. & Tilgner, A. 2022 Staircase formation in unstably stratified double diffusive finger convection. Phys. Fluids 34 (11), 116605.10.1063/5.0122882CrossRefGoogle Scholar
Schmitt, R.W. 1979 The growth rate of super-critical salt fingers. Deep-Sea Res. 26 (1), 23–40.10.1016/0198-0149(79)90083-9CrossRefGoogle Scholar
Schmitt, R.W. 1994 Double diffusion in oceanography. Annu. Rev. Fluid Mech. 26 (1), 255–285.CrossRefGoogle Scholar
Schmitt, R.W. 2003 Observational and laboratory insights into salt finger convection. Prog. Oceanogr. 56 (3–4), 419–433.CrossRefGoogle Scholar
Schmitt, R.W. 2011 Thermohaline convection at density ratios below one: a new regime for salt fingers. J. Mar. Res. 69 (4–6), 779–795.10.1357/002224011799849471CrossRefGoogle Scholar
Schmitt, R.W., Ledwell, J.R., Montgomery, E.T., Polzin, K.L. & Toole, J.M. 2005 Enhanced diapycnal mixing by salt fingers in the thermocline of the tropical Atlantic. Science 308 (5722), 685–688.10.1126/science.1108678CrossRefGoogle ScholarPubMed
Sreenivas, K.R., Singh, O.P. & Srinivasan, J. 2009 On the relationship between finger width, velocity, and fluxes in thermohaline convection. Phys. Fluids 21, 026601.10.1063/1.3070527CrossRefGoogle Scholar
Stellmach, S., Traxler, A., Garaud, P., Brummell, N. & Radko, T. 2011 Dynamics of fingering convection. Part 2. The formation of thermohaline staircases. J. Fluid Mech. 677, 554–571.CrossRefGoogle Scholar
Stern, M.E. 1960 The salt-fountain and thermohaline convection. Tellus 12 (2), 172–175.CrossRefGoogle Scholar
Stern, M.E. 1969 Collective instability of salt fingers. J. Fluid Mech. 35, 209–218.CrossRefGoogle Scholar
Stern, M.E., Radko, T. & Simeonov, J. 2001 Salt fingers in an unbounded thermocline. J. Mar. Res. 59, 355–390.CrossRefGoogle Scholar
Sun, H., Yang, Q. & Tian, J. 2018 Microstructure measurements and finescale parameterization assessment of turbulent mixing in the northern South China Sea. J. Oceanogr. 74 (5), 485–498.CrossRefGoogle Scholar
Taylor, J. & Bucens, P. 1989 Laboratory experiments on the structure of salt fingers. Deep-Sea Res. 36 (11), 1675–1704.CrossRefGoogle Scholar
Traxler, A., Stellmach, S., Garaud, P., Radko, T. & Brummell, N. 2011 Dynamics of fingering convection. Part 1. Small-scale fluxes and large-scale instabilities. J. Fluid Mech. 677, 530–553.10.1017/jfm.2011.98CrossRefGoogle Scholar
Turner, J.S. 1967 Salt fingers across a density interface. Deep-Sea Res. 14, 599–611.Google Scholar
Van Der Poel, E.P., Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2014 Effect of velocity boundary conditions on the heat transfer and flow topology in two-dimensional Rayleigh–Bénard convection. Phys. Rev. E 90 (1), 013017.10.1103/PhysRevE.90.013017CrossRefGoogle ScholarPubMed
Yang, Y., Chen, W.Y., Verzicco, R. & Lohse, D. 2020 Multiple states and transport properties of double-diffusive convection turbulence. Proc. Natl Acad. Sci. USA 117 (26), 14676–14681.CrossRefGoogle ScholarPubMed
Yang, Y., van der Poel, E.P., Ostilla-Mónico, R., Sun, C., Verzicco, R., Grossmann, S. & Lohse, D. 2015 Salinity transfer in bounded double diffusive convection. J. Fluid Mech. 768, 476–491.CrossRefGoogle Scholar
Yang, Y., Verzicco, R. & Lohse, D. 2016 a From convection rolls to finger convection in double-diffusive turbulence. Proc. Natl Acad. Sci. USA 113 (1), 69–73.CrossRefGoogle ScholarPubMed
Yang, Y., Verzicco, R. & Lohse, D. 2016 b Scaling laws and flow structures of double diffusive convection in the finger regime. J. Fluid Mech. 802, 667–689.10.1017/jfm.2016.484CrossRefGoogle Scholar
Yang, Y., Verzicco, R. & Lohse, D. 2016 c Vertically bounded double diffusive convection in the finger regime: comparing no-slip versus free-slip boundary conditions. Phys. Rev. Lett. 117, 184501.CrossRefGoogle ScholarPubMed
Yoshida, J. & Nagashima, H. 2003 Numerical experiments on salt-finger convection. Prog. Oceanogr. 56 (3–4), 435–459.CrossRefGoogle Scholar
You, Y. 2002 A global ocean climatological atlas of the Turner angle: implications for double-diffusion and water-mass structure. Deep-Sea Res. 49 (11), 2075–2093.CrossRefGoogle Scholar