Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T03:39:57.428Z Has data issue: false hasContentIssue false
  • English
  • Français

On the transition pattern of the oblique detonation structure

Published online by Cambridge University Press:  26 October 2012

Hong Hui Teng  and
Zong Lin Jiang
Hong Hui Teng*
Affiliation:
State Key Lab of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing, 100190, China
Zong Lin Jiang
Affiliation:
State Key Lab of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing, 100190, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Oblique detonation waves are simulated to study the evolution of their morphology as gasdynamic and chemical parameters are varied. Although two kinds of transition pattern have previously been observed, specifically an abrupt transition and a smooth one, the determining factors for the transition pattern are still unclear. Numerical results show that the transition pattern is influenced by the inflow Mach number, chemical activation energy and heat release. Despite the fact that these parameters were known to influence the detonation instability, the transition pattern variation cannot be predicted according to the instability criterion. In this study, the difference in the oblique shock and detonation angles is proposed as the criterion to determine the transition pattern with the aid of shock-polar analysis. It is found that the smooth transition will appear when the angle difference is small, while the abrupt transition will occur when the difference is large. 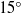The shift from the smooth transition to the abrupt transition occurs when the angle difference is about $1{5}^{\ensuremath{\circ} } $–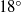$1{8}^{\ensuremath{\circ} } $. The previously proposed criterion using the characteristic time ratio is also examined and compared with the present angle difference criterion, and the latter is proved to provide better results.

JFM classification

Reacting Flows: Detonations Reacting Flows: Reacting Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 659 - 669
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Broda, J. C. 1993 An experimental study of oblique detonation waves. PhD thesis, University of Connecticut.Google Scholar
Choi, J. Y., Kim, D. W., Jeung, I. S., Ma, F. & Yang, V. 2007 Cell-like structure of unstable oblique detonation wave from high-resolution numerical simulation. Proc. Combust. Inst. 31, 2473–2480.CrossRefGoogle Scholar
Choi, J. Y., Shin, E. J. & Jeung, I. S. 2009 Unstable combustion induced by oblique shock waves at the non-attaching condition of the oblique detonation wave. Proc. Combust. Inst. 32, 2387–2396.Google Scholar
Daimon, Y. & Matsuo, A. 2004 Analogy between wedge-induced steady oblique detonation and one-dimensional piston-supported unsteady detonation. Sci. Technol. Energ. Mater. 65, 111–115.Google Scholar
Figueira da Silva, L. & Deshaies, B. 2000 Stabilization of an oblique detonation wave by a wedge: a parametric numerical study. Combust. Flame 121, 152–166.CrossRefGoogle Scholar
Fusina, G., Sislian, J. P. & Parent, B. 2005 Formation and stability of near Chapman–Jouguet standing oblique detonation waves. AIAA J. 43, 1591–1604.CrossRefGoogle Scholar
Kailasanath, K. 2003 Recent developments in the research on pulse detonation engines. AIAA J. 41, 154–159.CrossRefGoogle Scholar
Li, C., Kailasanath, K. & Oran, E. S. 1993 Effects of boundary layers on oblique-detonation structures. AIAA Paper 1993-0450.CrossRefGoogle Scholar
Li, C., Kailasanath, K. & Oran, E. S. 1994 Detonation structures behind oblique shocks. Phys. Fluids 6, 1600–1611.Google Scholar
Maeda, S., Inada, R., Kasahara, J. & Matsuo, A. 2011 Visualization of the non-steady state oblique detonation wave phenomena around hypersonic spherical projectile. Proc. Combust. Inst. 33, 2343–2349.Google Scholar
Nettleton, M. A. 2000 The applications of unsteady, multi-dimensional studies of detonation waves to ram accelerators. Shock Waves 10, 9–22.CrossRefGoogle Scholar
Ng, H. D. & Lee, J. H. S. 2003 Direct initiation of detonation with a multi-step reaction scheme. J. Fluid Mech. 476, 179–211.Google Scholar
Papalexandris, M. V. 2000 Numerical study of wedge-induced detonations. Combust. Flame 120, 526–538.CrossRefGoogle Scholar
Roy, G. D., Frolov, S. M., Borisov, A. A. & Netzer, D. W. 2004 Pulse detonation propulsion: challenges, current status, and future perspective. Prog. Energy Combust. Sci. 30, 545–672.CrossRefGoogle Scholar
Sharpe, G. J. 2001 Transverse waves in numerical simulations of cellular detonations. J. Fluid Mech. 447, 31–51.CrossRefGoogle Scholar
Short, M. & Quirk, J. J. 1997 On the nonlinear stability and detonability limit of a detonation wave for a model three-step chain-branching reaction. J. Fluid Mech. 339, 89–119.CrossRefGoogle Scholar
Toro, E. F. 1999 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer.Google Scholar
Viguier, C., Figueira da Silva, L., Desbordes, D. & Deshaies, B. 1997 Onset of oblique detonation waves: comparison between experimental and numerical results for hydrogen–air mixtures. Proc. Combust. Inst. 26, 3023–3031.Google Scholar
Vlasenko, V. V. & Sabelnikov, V. A. 1995 Numerical simulation of inviscid flows with hydrogen combustion behind shock waves and in detonation waves. Combust. Explos. Shock Waves 31, 376–389.Google Scholar
Wang, A. F., Zhao, W. & Jiang, Z. L. 2011 The criterion of the existence or inexistence of transverse shock wave at wedge supported oblique detonation wave. Acta Mech. Sinica 27, 611–619.Google Scholar