Article contents
On the transition from finite-volume negatively buoyant releases to continuous fountains
Published online by Cambridge University Press: 30 March 2012
Abstract
An experimental investigation to identify the source conditions that distinguish finite-volume negatively buoyant fluid projectile behaviour from fountain behaviour in quiescent environments of uniform density is described. Finite-volume releases are governed by their source Froude number 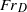 and the aspect ratio
and the aspect ratio 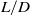 of the release, where
of the release, where 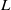 denotes the length of the column of fluid dispensed vertically from the nozzle of diameter
denotes the length of the column of fluid dispensed vertically from the nozzle of diameter 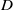 . We establish the influence of
. We establish the influence of 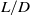 on the peak rise heights of a release formed by dispensing saline solution into fresh water for
on the peak rise heights of a release formed by dispensing saline solution into fresh water for 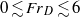 and
and 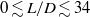 . Within these ranges, we determine the source conditions for which a flow may be regarded, in terms of the initial rise height attained, as either finite-volume or continuous flux. The critical aspect ratio
. Within these ranges, we determine the source conditions for which a flow may be regarded, in terms of the initial rise height attained, as either finite-volume or continuous flux. The critical aspect ratio 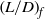 , for a given
, for a given  , which when exceeded no longer influenced release behaviour, led to the determination of
, which when exceeded no longer influenced release behaviour, led to the determination of 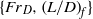 paired source conditions that give rise to solely Froude-number-dependent, i.e. fountain-like, behaviour. As such, we make the link between finite-volume releases and continuous fountains. The
paired source conditions that give rise to solely Froude-number-dependent, i.e. fountain-like, behaviour. As such, we make the link between finite-volume releases and continuous fountains. The 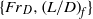 pairs led us directly to the classification of a
pairs led us directly to the classification of a 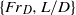 space from which source conditions giving rise to either negatively buoyant projectiles or fountains may be readily identified. The variation of
space from which source conditions giving rise to either negatively buoyant projectiles or fountains may be readily identified. The variation of 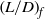 with
with 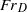 corresponds closely to established fountain regimes of very weak, weak and forced fountains. Moreover, our results indicate that the formation or otherwise of a primary vortex, as fluid is ejected, has a profound influence on the length of the dispensed fluid column that is necessary to achieve rise heights equal to fountain rise heights.
corresponds closely to established fountain regimes of very weak, weak and forced fountains. Moreover, our results indicate that the formation or otherwise of a primary vortex, as fluid is ejected, has a profound influence on the length of the dispensed fluid column that is necessary to achieve rise heights equal to fountain rise heights.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 5
- Cited by


