Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Keylock, Christopher J.
2019.
Turbulence at the Lee bound: maximally non-normal vortex filaments and the decay of a local dissipation rate.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
283.
Das, Rishita
and
Girimaji, Sharath S
2020.
Revisiting turbulence small-scale behavior using velocity gradient triple decomposition.
New Journal of Physics,
Vol. 22,
Issue. 6,
p.
063015.
Das, Rishita
and
Girimaji, Sharath S.
2020.
Characterization of velocity-gradient dynamics in incompressible turbulence using local streamline geometry.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Yeung, P. K.
and
Ravikumar, K.
2020.
Advancing understanding of turbulence through extreme-scale computation: Intermittency and simulations at large problem sizes.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Sharma, Bajrang
Das, Rishita
and
Girimaji, Sharath S.
2021.
Local vortex line topology and geometry in turbulence.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Dabbagh, F.
and
Schneiderbauer, S.
2021.
Small-scale flow topologies, pseudo-turbulence, and impact on filtered drag models in turbulent fluidization.
Physical Review Fluids,
Vol. 6,
Issue. 7,
Sreenivasan, Katepalli R.
and
Yakhot, Victor
2021.
Dynamics of three-dimensional turbulence from Navier-Stokes equations.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Das, Rishita
and
Girimaji, Sharath S.
2022.
The effect of large-scale forcing on small-scale dynamics of incompressible turbulence.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Ghira, A. A.
Elsinga, G. E.
and
da Silva, C. B.
2022.
Characteristics of the intense vorticity structures in isotropic turbulence at high Reynolds numbers.
Physical Review Fluids,
Vol. 7,
Issue. 10,
2023.
New features in turbulence dissipation.
Physics of Fluids,
Vol. 35,
Issue. 4,
Buaria, Dhawal
and
Sreenivasan, Katepalli R.
2023.
Forecasting small-scale dynamics of fluid turbulence using deep neural networks.
Proceedings of the National Academy of Sciences,
Vol. 120,
Issue. 30,
Liu, Feng
Wu, Zhuangzhuang
Lv, Pengfei
Yang, Wei
and
Zhou, Yi
2023.
Evolution of the velocity gradient invariants in homogeneous isotropic turbulence with an inverse energy cascade.
Physics of Fluids,
Vol. 35,
Issue. 2,
Elsinga, G.E.
Ishihara, T.
and
Hunt, J.C.R.
2023.
Intermittency across Reynolds numbers – the influence of large-scale shear layers on the scaling of the enstrophy and dissipation in homogenous isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 974,
Issue. ,
Saldana, Manuel
Gallegos, Sandra
Gálvez, Edelmira
Castillo, Jonathan
Salinas-Rodríguez, Eleazar
Cerecedo-Sáenz, Eduardo
Hernández-Ávila, Juan
Navarra, Alessandro
and
Toro, Norman
2024.
The Reynolds Number: A Journey from Its Origin to Modern Applications.
Fluids,
Vol. 9,
Issue. 12,
p.
299.
Arun, Rahul
and
Colonius, Tim
2024.
Velocity gradient analysis of a head-on vortex ring collision.
Journal of Fluid Mechanics,
Vol. 982,
Issue. ,
Das, Rishita
and
Girimaji, Sharath S.
2024.
Data-driven model for Lagrangian evolution of velocity gradients in incompressible turbulent flows.
Journal of Fluid Mechanics,
Vol. 984,
Issue. ,
Wu, Geyi
and
Xu, Chunxiao
2024.
Characterization and evolution of local streamline geometry in an incompressible turbulent channel flow.
Physics of Fluids,
Vol. 36,
Issue. 2,
Johnson, Perry L.
and
Wilczek, Michael
2024.
Multiscale Velocity Gradients in Turbulence.
Annual Review of Fluid Mechanics,
Vol. 56,
Issue. 1,
p.
463.
Capocci, Damiano
2025.
Expressing turbulent kinetic energy as coarse-grained enstrophy or strain deformations.
Physical Review Fluids,
Vol. 10,
Issue. 2,
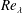 $Re_{\unicode[STIX]{x1D706}}$). The analysis factorizes the velocity gradient (
$Re_{\unicode[STIX]{x1D706}}$). The analysis factorizes the velocity gradient (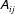 $\unicode[STIX]{x1D608}_{ij}$) into the magnitude (
$\unicode[STIX]{x1D608}_{ij}$) into the magnitude (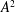 $A^{2}$) and normalized-gradient tensor (
$A^{2}$) and normalized-gradient tensor (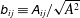 $\unicode[STIX]{x1D623}_{ij}\equiv \unicode[STIX]{x1D608}_{ij}/\sqrt{A^{2}}$). The focus is on bounded
$\unicode[STIX]{x1D623}_{ij}\equiv \unicode[STIX]{x1D608}_{ij}/\sqrt{A^{2}}$). The focus is on bounded 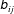 $\unicode[STIX]{x1D623}_{ij}$ as (i) it describes small-scale structure and local streamline topology, and (ii) its dynamics is shown to determine magnitude evolution. Using direct numerical simulation (DNS) data, the moments and probability distributions of
$\unicode[STIX]{x1D623}_{ij}$ as (i) it describes small-scale structure and local streamline topology, and (ii) its dynamics is shown to determine magnitude evolution. Using direct numerical simulation (DNS) data, the moments and probability distributions of 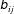 $\unicode[STIX]{x1D623}_{ij}$ and its scalar invariants are shown to attain
$\unicode[STIX]{x1D623}_{ij}$ and its scalar invariants are shown to attain 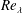 $Re_{\unicode[STIX]{x1D706}}$ independence. The critical values beyond which each feature attains
$Re_{\unicode[STIX]{x1D706}}$ independence. The critical values beyond which each feature attains 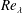 $Re_{\unicode[STIX]{x1D706}}$ independence are established. We proceed to characterize the
$Re_{\unicode[STIX]{x1D706}}$ independence are established. We proceed to characterize the 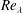 $Re_{\unicode[STIX]{x1D706}}$ dependence of
$Re_{\unicode[STIX]{x1D706}}$ dependence of 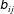 $\unicode[STIX]{x1D623}_{ij}$-conditioned statistics of key non-local pressure and viscous processes. Overall, the analysis provides further insight into velocity-gradient dynamics and offers an alternative framework for investigating intermittency, multifractal behaviour and for developing closure models.
$\unicode[STIX]{x1D623}_{ij}$-conditioned statistics of key non-local pressure and viscous processes. Overall, the analysis provides further insight into velocity-gradient dynamics and offers an alternative framework for investigating intermittency, multifractal behaviour and for developing closure models.

