Hostname: page-component-66644f4456-2xp4c Total loading time: 0 Render date: 2025-02-12T22:39:53.838Z Has data issue: true hasContentIssue false
  • English
  • Français

On the relationship between the non-local clustering mechanism and preferential concentration

Published online by Cambridge University Press:  03 September 2015

Andrew D. Bragg ,
Peter J. Ireland  and
Lance R. Collins
Andrew D. Bragg
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Peter J. Ireland
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Lance R. Collins
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

‘Preferential concentration’ (Squires & Eaton, Phys. Fluids, vol. A3, 1991, pp. 1169–1178) refers to the clustering of inertial particles in the high strain, low-rotation regions of turbulence. The ‘centrifuge mechanism’ of Maxey (J. Fluid Mech., vol. 174, 1987, pp. 441–465) appears to explain this phenomenon. In a recent paper, Bragg & Collins (New J. Phys., vol. 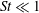16, 2014, 055013) showed that the centrifuge mechanism is dominant only in the regime $St\ll 1$, where 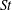$St$ is the Stokes number based on the Kolmogorov time scale. Outside this regime, the centrifuge mechanism gives way to a non-local, path history symmetry breaking mechanism. However, despite the change in the clustering mechanism, the instantaneous particle positions continue to correlate with high strain, low-rotation regions of the turbulence. In this paper, we analyse the exact equation governing the radial distribution function and show how the non-local clustering mechanism is influenced by, but not dependent upon, the preferential sampling of the fluid velocity gradient tensor along the particle path histories in such a way as to generate a bias for clustering in high strain regions of the turbulence. We also show how the non-local mechanism still generates clustering, but without preferential concentration, in the limit where the time scales of the fluid velocity gradient tensor measured along the inertial particle trajectories approaches zero (such as white noise flows or for particles in turbulence settling under strong gravity). Finally, we use data from a direct numerical simulation of inertial particles suspended in Navier–Stokes turbulence to validate the arguments presented in this study.

JFM classification

Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 327 - 343
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Bec, J. 2003 Fractal clustering of inertial particles in random flows. Phys. Fluids 15, L81–L84.CrossRefGoogle Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A. S. & Toschi, F. 2010 Intermittency in the velocity distribution of heavy particles in turbulence. J. Fluid Mech. 646, 527–536.CrossRefGoogle Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112, 184501.Google Scholar
Bragg, A. D. & Collins, L. R. 2014 New insights from comparing statistical theories for inertial particles in turbulence. Part I: spatial distribution of particles. New J. Phys. 16, 055013.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R.2014 Forward and backward in time dispersion of fluid and inertial particles in isotropic turbulence. arXiv:1403.5502.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.CrossRefGoogle Scholar
Chun, J., Koch, D. L., Rani, S., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.CrossRefGoogle Scholar
Computational and Information Systems Laboratory2012, Yellowstone: IBM iDataPlex System (University Community Computing), http://n2t.net/ark:/85065/d7wd3xhc.Google Scholar
Duncan, K., Mehlig, B., Östlund, S. & Wilkinson, M. 2005 Clustering by mixing flows. Phys. Rev. Lett. 95, 240602.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Falkovich, G., Fouxon, A. & Stepanov, M. G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419, 151–154.CrossRefGoogle ScholarPubMed
Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. J. Atmos. Sci. 64, 4497–4505.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids A 2, 242–256.Google Scholar
Gustavsson, K. & Mehlig, B. 2011a Distribution of relative velocities in turbulent aerosols. Phys. Rev. E 84, 045304.Google Scholar
Gustavsson, K. & Mehlig, B. 2011b Ergodic and non-ergodic clustering of inertial particles. Eur. Phys. Lett. 96, 60012.CrossRefGoogle Scholar
Gustavsson, K. & Mehlig, B. 2014 Clustering of particles falling in a turbulent flow. Phys. Rev. Lett. 112, 214501.Google Scholar
van Hinsberg, M. A. T., Thije Boonkkamp, J. H. M., Toschi, F. & Clercx, H. J. H. 2012 On the efficiency and accuracy of interpolation methods for spectral codes. SIAM J. Sci. Comput. 34 (4), B479–B498.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R.2015 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part I: simulations without gravitational effects. arXiv e-prints.Google Scholar
Ireland, P. J., Vaithianathan, T., Sukheswalla, P. S., Ray, B. & Collins, L. R. 2013 Highly parallel particle-laden flow solver for turbulence research. Comput. Fluids 76, 170–177.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds-number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Maxey, M. R. & Corrsin, S. 1986 Gravitational settling of aerosol particles in randomly oriented cellular flow fields. J. Atmos. Sci. 43, 1112–1134.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
McQuarrie, D. A. 1976 Statistical Mechanics. Harper & Row.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ray, B. & Collins, L. R. 2013 Investigation of sub-Kolmogorov inertial particle pair dynamics in turbulence using novel satellite particle simulations. J. Fluid Mech. 720, 192–211.CrossRefGoogle Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.CrossRefGoogle Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012a Inertial particle acceleration statistics in turbulence: effects of filtering, biased sampling and flow topology. Phys. Fluids 24, 083302.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012b Inertial particle relative velocity statistics in homogeneous isotropic turbulence. J. Fluid Mech. 696, 45–66.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic, particle-laden turbulent suspension. Part I. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modeling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.Google Scholar
Witkowska, A., Brasseur, J. G. & Juvé, D. 1997 Numerical study of noise from isotropic turbulence. J. Comput. Acoust. 5, 317–336.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2003 Pair dispersion and preferential concentration of particles in isotropic turbulence. Phys. Fluids 15, 1776–1787.CrossRefGoogle Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2007 Refinement of the probability density function model for preferential concentration of aerosol particles in isotropic turbulence. Phys. Fluids 19, 113308.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11, 103018.Google Scholar