Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T15:45:14.494Z Has data issue: false hasContentIssue false
  • English
  • Français

On the propagation of acoustic–gravity waves under elastic ice sheets

Published online by Cambridge University Press:  05 January 2018

Ali Abdolali Open the ORCID record for Ali Abdolali [Opens in a new window] ,
Usama Kadri ,
Wade Parsons  and
James T. Kirby
Ali Abdolali*
Affiliation:
NWS/NCEP/Environmental Modeling Center, National Oceanic and Atmospheric Administration (NOAA), College Park, MD 20740, USA University Corporation for Atmospheric Research (UCAR), Boulder, CO 80301, USA
Usama Kadri
Affiliation:
School of Mathematics, Cardiff University, CardiffCF24 4AG, UK Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Wade Parsons
Affiliation:
Faculty of Engineering and Applied Science, Memorial University of Newfoundland, 240 Prince Philip Drive, St. John’s, NL A1B 3X5, Canada
James T. Kirby
Affiliation:
Center for Applied Coastal Research, Department of Civil and Environmental Engineering, University of Delaware, Newark, DE 19716, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The propagation of wave disturbances in water of varying depth bounded above by ice sheets is discussed, accounting for gravity, compressibility and elasticity effects. Considering the more realistic scenario of elastic ice sheets reveals a continuous spectrum of acoustic–gravity modes that propagate even below the cutoff frequency of the rigid surface solution where surface (gravity) waves cannot exist. 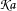The balance between gravitational forces and oscillations in the ice sheet defines a new dimensionless quantity $\mathfrak{Ka}$. When the ice sheet is relatively thin and the prescribed frequency is relatively low (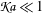$\mathfrak{Ka}\ll 1$), the free-surface bottom-pressure solution is retrieved in full. However, thicker ice sheets or propagation of relatively higher frequency modes (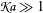$\mathfrak{Ka}\gg 1$) alter the solution fundamentally, which is reflected in an amplified asymmetric signature and different characteristics of the eigenvalues, such that the bottom pressure is amplified when acoustic–gravity waves are transmitted to shallower waters. To analyse these scenarios, an analytical solution and a depth-integrated equation are derived for the cases of constant and varying depths, respectively. Together, these are capable of modelling realistic ocean geometries and an inhomogeneous distribution of ice sheets.

JFM classification

Compressible Flows: Compressible Flows Geophysical and Geological Flows: Geophysical and Geological Flows Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 837 , 25 February 2018 , pp. 640 - 656
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdolali, A. & Kirby, J. T. 2017 Role of compressibility on tsunami propagation. J. Geophys. Res. Oceans 122, doi:10.1002/2017JC013054.Google Scholar
Abdolali, A., Kirby, J. T. & Bellotti, G. 2015 Depth-integrated equation for hydro-acoustic waves with bottom damping. J. Fluid Mech. 766, R1.Google Scholar
Caplan-Auerbach, J., Dziak, R. P., Bohnenstiehl, D. R., Chadwick, W. W. & Lau, T.-K. 2014 Hydroacoustic investigation of submarine landslides at West Mata volcano, Lau Basin. Geophys. Res. Lett. 41 (16), 5927–5934; 2014GL060964.10.1002/2014GL060964Google Scholar
Cecioni, C., Bellotti, G., Romano, A., Abdolali, A. & Sammarco, P. 2014 Tsunami early warning system based on real-time measurements of hydro-acoustic waves. Procedia Engng 70 (C), 311–320.Google Scholar
Chierici, F., Pignagnoli, L. & Embriaco, D. 2010 Modeling of the hydroacoustic signal and tsunami wave generated by seafloor motion including a porous seabed. J. Geophys. Res. 115, C03015.Google Scholar
Eyov, E., Klar, A., Kadri, U. & Stiassnie, M. 2013 Progressive waves in a compressible-ocean with an elastic bottom. Wave Motion 50 (5), 929–939.10.1016/j.wavemoti.2013.03.003Google Scholar
Hansen, J. 2007 Climate catastrophe. New Sci. 195 (2614), 30–34.Google Scholar
Hendin, G. & Stiassnie, M. 2013 Tsunami and acoustic–gravity waves in water of constant depth. Phys. Fluids 25 (8), 086103.Google Scholar
Hosking, R. J., Sneyd, A. D. & Waugh, D. W. 1988 Viscoelastic response of a floating ice plate to a steadily moving load. J. Fluid Mech. 196, 409–430.10.1017/S0022112088002757Google Scholar
Kadri, U. 2014 Deep ocean water transport by acoustic-gravity waves. J. Geophys. Res. 119 (11), 7925–7930.Google Scholar
Kadri, U. 2015 Wave motion in a heavy compressible fluid: revisited. Eur. J. Mech. (B/Fluids) 49, Part A, 50–57.Google Scholar
Kadri, U. 2016a Generation of hydroacoustic waves by an oscillating ice block in arctic zones. Adv. Acoust. Vib. 2016, 1–7.Google Scholar
Kadri, U. 2016b Triad resonance between a surface-gravity wave and two high frequency hydro-acoustic waves. Eur. J. Mech. (B/Fluids) 55, Part 1, 157–161.Google Scholar
Kadri, U. 2017 Tsunami mitigation by resonant triad interaction with acoustic–gravity waves. Heliyon 3 (1), e00234.Google Scholar
Kadri, U. & Akylas, T. R. 2016 On resonant triad interactions of acoustic-gravity waves. J. Fluid Mech. 788, R1.Google Scholar
Kadri, U. & Stiassnie, M. 2012 Acoustic-gravity waves interacting with the shelf break. J. Geophys. Res. 117 (C3), c03035.Google Scholar
Kadri, U. & Stiassnie, M. 2013 Generation of an acoustic-gravity wave by two gravity waves, and their subsequent mutual interaction. J. Fluid Mech. 735, R6.Google Scholar
Kirby, J. T. 1992 Water waves in variable depth under continuous sea ice. In Proceedings of the Second International Conference on Offshore and Polar Engineering Conference, pp. 70–76. International Society of Offshore and Polar Engineers.Google Scholar
Oliveira, T. C. A. & Kadri, U. 2016 Pressure field induced in the water column by acoustic-gravity waves generated from sea bottom motion. J. Geophys. Res. 121 (10), 7795–7803.Google Scholar
Renzi, E. & Dias, F. 2014 Hydro-acoustic precursors of gravity waves generated by surface pressure disturbances localised in space and time. J. Fluid Mech. 754, 250–262.Google Scholar
Sammarco, P., Cecioni, C., Bellotti, G. & Abdolali, A. 2013 Depth-integrated equation for large-scale modelling of low-frequency hydroacoustic waves. J. Fluid Mech. 722, R6.10.1017/jfm.2013.153Google Scholar
Schulkes, R. M. S. M., Hosking, R. J. & Sneyd, A. D. 1987 Waves due to a steadily moving source on a floating ice plate. Part 2. J. Fluid Mech. 180, 297–318.Google Scholar
Stiassnie, M. 2010 Tsunamis and acoustic-gravity waves from underwater earthquakes. J. Engng Maths 67 (1–2), 23–32.10.1007/s10665-009-9323-xGoogle Scholar
Yamamoto, T. 1982 Gravity waves and acoustic waves generated by submarine earthquakes. Intl J. Soil Dyn. Earthq. Engng 1 (2), 75–82.Google Scholar
Zakharov, D. D. 2008 Orthogonality of 3D guided waves in viscoelastic laminates and far field evaluation to a local acoustic source. Intl J. Solids Struct. 45 (6), 1788–1803.Google Scholar