Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T18:32:44.510Z Has data issue: false hasContentIssue false
  • English
  • Français

On the lifetime of a pancake anticyclone in a rotating stratified flow

Published online by Cambridge University Press:  13 September 2016

Giulio Facchini Open the ORCID record for Giulio Facchini [Opens in a new window]  and
Michael Le Bars
Giulio Facchini*
Affiliation:
Aix-Marseille Université, CNRS, École Centrale Marseille, Institut de Recherche sur les Phénomènes Hors Équilibre, UMR 7342, 49 rue F. Joliot Curie, 13013 Marseille, France
Michael Le Bars
Affiliation:
Aix-Marseille Université, CNRS, École Centrale Marseille, Institut de Recherche sur les Phénomènes Hors Équilibre, UMR 7342, 49 rue F. Joliot Curie, 13013 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental study of the time evolution of an isolated anticyclonic pancake vortex in a laboratory rotating stratified flow. Motivations come from the variety of compact anticyclones observed to form and persist for a strikingly long lifetime in geophysical and astrophysical settings combining rotation and stratification. We generate anticyclones by injecting a small amount of isodense fluid at the centre of a rotating tank filled with salty water linearly stratified in density. The velocity field is measured by particle image velocimetry in the vortex equatorial plane. Our two control parameters are the Coriolis parameter 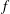$f$ and the Brunt–Väisälä frequency 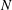$N$. We observe that anticyclones always slowly decay by viscous diffusion, spreading mainly in the horizontal direction irrespective of the initial aspect ratio. This behaviour is correctly explained by a linear analytical model in the limit of small Rossby and Ekman numbers, where density and velocity equations reduce to a single equation for the pressure. In particular for 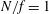$N/f=1$, this equation ultimately simplifies to a radial diffusion equation, which admits an analytical self-similar solution. Direct numerical simulations further confirm the theoretical predictions that are not accessible to laboratory measurements. Notably, they show that the azimuthal shear stress generates secondary circulations, which advect the density anomaly: this mechanism is responsible for the slow time evolution, rather than the classical viscous dissipation of the azimuthal kinetic energy. The importance of density diffusivity is also analysed, showing that the product of the Schmidt and Burger numbers – rather than the bare Schmidt number – quantifies the importance of salt diffusion. Finally, a brief application to oceanic Meddies is considered.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 688 - 711
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armi, L., Hebert, D., Oakey, N., Price, J. F., Richardson, P. L., Rossby, H. T. & Ruddick, B. 1989 Two years in the life of a mediterranean salt lens. J. Phys. Oceanogr. 19 (3), 354–370.2.0.CO;2>CrossRefGoogle Scholar
Armi, L. & Zenk, W. 1984 Large lenses of highly saline mediterranean water. J. Phys. Oceanogr. 14 (10), 1560–1576.Google Scholar
Aubert, O., Le Bars, M., Le Gal, P. & Marcus, P. S. 2012 The universal aspect ratio of vortices in rotating stratified flows: experiments and observations. J. Fluid Mech. 706, 34–45.Google Scholar
Barranco, J. A. & Marcus, P. S. 2005 Three-dimensional vortices in stratified protoplanetary disks. Astrophys. J. 623 (2), 1157–1170.Google Scholar
Bashmachnikov, I., Neves, F., Calheiros, T. & Carton, X. 2015 Properties and pathways of mediterranean water eddies in the atlantic. Prog. Oceanogr. 137, 149–172.Google Scholar
Beckers, M., Verzicco, R., Clercx, H. J. H. & Van Heijst, G. J. F. 2001 Dynamics of pancake-like vortices in a stratified fluid: experiments, model and numerical simulations. J. Fluid Mech. 433, 1–27.CrossRefGoogle Scholar
Bogucki, D. J., Jones, B. H. & Carr, M.-E. 2005 Remote measurements of horizontal eddy diffusivity. J. Atmos. Ocean. Technol. 22 (9), 1373–1380.Google Scholar
Canuto, V. M., Howard, A., Cheng, Y. & Dubovikov, M. S. 2001 Ocean turbulence. Part i: one-point closure model-momentum and heat vertical diffusivities. J. Phys. Oceanogr. 31 (6), 1413–1426.2.0.CO;2>CrossRefGoogle Scholar
Colin de Verdiere, A. 1992 On the southward motion of mediterranean salt lenses. J. Phys. Oceanogr. 22 (4), 413–420.Google Scholar
Dritschel, D. G., de la Torre Jurez, M. & Ambaum, M. H. P. 1999 The three-dimensional vortical nature of atmospheric and oceanic turbulent flows. Phys. Fluids 11 (6), 1512–1520.CrossRefGoogle Scholar
Gill, A. E. 1981 Homogeneous intrusions in a rotating stratified fluid. J. Fluid Mech. 103, 275–295.Google Scholar
Godoy-Diana, R. & Chomaz, J.-M. 2003 Effect of the schmidt number on the diffusion of axisymmetric pancake vortices in a stratified fluid. Phys. Fluids 15 (4), 1058–1064.Google Scholar
Griffiths, R. W. & Linden, P. F. 1981 The stability of vortices in a rotating, stratified fluid. J. Fluid Mech. 105, 283–316.Google Scholar
Hassanzadeh, P., Marcus, P. S. & Le Gal, P. 2012 The universal aspect ratio of vortices in rotating stratified flows: theory and simulation. J. Fluid Mech. 706, 46–57.Google Scholar
Hebert, D., Oakey, N. & Ruddick, B. 1990 Evolution of a mediterranean salt lens: Scalar properties. J. Phys. Oceanogr. 20 (9), 1468–1483.Google Scholar
Hedstrom, K. & Armi, L. 1988 An experimental study of homogeneous lenses in a stratified rotating fluid. J. Fluid Mech. 191, 535–556.Google Scholar
Kloosterziel, R. C. 1990 On the large time asymptotics of the diffusion equation on infinite domains. J. Engng Maths 24 (3), 213–236.Google Scholar
Kloosterziel, R. C. & van Heijst, G. J. F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.Google Scholar
Large, W. G. & Gent, P. R. 1999 Validation of vertical mixing in an equatorial ocean model using large eddy simulations and observations. J. Phys. Oceanogr. 29 (3), 449–464.Google Scholar
Ledwell, J. R., Watson, A. J. & Law, C. S. 1993 Evidence for slow mixing across the pycnocline from an open-ocean tracer-release experiment. Nature 364 (6439), 701–703.Google Scholar
Mahdinia, M., Hassanzadeh, P., Marcus, P. S. & Jiang, C.-H.2016 Stability of 3D Gaussian vortices in rotating stratified Boussinesq flows: linear analysis. arXiv:1605.06859.Google Scholar
Marcus, P. S. 1993 Jupiter’s great red spot and other vortices. Annu. Rev. Astron. Astrophys. 31, 523–569.Google Scholar
McWilliams, J. C. 1985 Submesoscale, coherent vortices in the ocean. Rev. Geophys. 23 (2), 165–182.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and treatment of errors due to high velocity gradients in particle image velocimetry. Exp. Fluids 35 (5), 408–421.CrossRefGoogle Scholar
Nguyen, H. Y., Hua, B. L., Schopp, R. & Carton, X. 2012 Slow quasigeostrophic unstable modes of a lens vortex in a continuously stratified flow. Geophys. Astrophys. Fluid Dyn. 106 (3), 305–319.Google Scholar
Oster, G. 1965 Density gradients. Sci. Am. 213, 70–76.Google Scholar
Reinaud, J. N., Dritschel, D. G. & Koudella, C. R. 2003 The shape of vortices in quasi-geostrophic turbulence. J. Fluid Mech. 474, 175–192.Google Scholar
Richardson, P. L., Bower, A. S. & Zenk, W. 2000 A census of Meddies tracked by floats. Prog. Oceanogr. 45, 209–250.CrossRefGoogle Scholar
Ruddick, B. & Hebert, D. 1988 The mixing of meddy ‘Sharon’.Small-Scale Mixing in the Ocean, Elesevier Oceanography Series, vol. 46, pp. 249–261.Google Scholar
Sundermeyer, M. A. & Ledwell, J. R. 2001 Lateral dispersion over the continental shelf: analysis of dye release experiments. J. Geophys. Res.: Oceans 106 (C5), 9603–9621.CrossRefGoogle Scholar
Ungarish, M. 2015 On the coupling between spin-up and aspect ratio of vortices in rotating stratified flows: a predictive model. J. Fluid Mech. 777, 461–481.Google Scholar
Yim, E.2015 Stability of columnar and pancake vortices in stratified-rotating fluids. PhD thesis, École polytechnique Laboratoire d’Hydrodynamique Palaiseau, France.Google Scholar