Article contents
On the free-surface flow of very steep forced solitary waves
Published online by Cambridge University Press: 13 December 2013
Abstract
The free-surface flow of very steep forced and unforced solitary waves is considered. The forcing is due to a distribution of pressure on the free surface. Four types of forced solution are identified which all approach the Stokes-limiting configuration of an included angle of 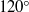 $12{0}^{\circ } $ and a stagnation point at the wave crests. For each type of forced solution the almost-highest wave does not contain the most energy, nor is it the fastest, similar to what has been observed previously in the unforced case. Nonlinear solutions are obtained by deriving and solving numerically a boundary integral equation. A weakly nonlinear approximation to the flow problem helps with the identification and classification of the forced types of solution, and their stability.
$12{0}^{\circ } $ and a stagnation point at the wave crests. For each type of forced solution the almost-highest wave does not contain the most energy, nor is it the fastest, similar to what has been observed previously in the unforced case. Nonlinear solutions are obtained by deriving and solving numerically a boundary integral equation. A weakly nonlinear approximation to the flow problem helps with the identification and classification of the forced types of solution, and their stability.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 9
- Cited by


