Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-14T04:23:00.137Z Has data issue: false hasContentIssue false
  • English
  • Français

On the emergence of secondary tones in airfoil noise

Published online by Cambridge University Press:  27 June 2023

Alex Sano Open the ORCID record for Alex Sano [Opens in a new window] ,
André V.G. Cavalieri Open the ORCID record for André V.G. Cavalieri [Opens in a new window] ,
André F.C. da Silva Open the ORCID record for André F.C. da Silva [Opens in a new window]  and
William R. Wolf Open the ORCID record for William R. Wolf [Opens in a new window]
Alex Sano*
Affiliation:
Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP 12228-900, Brazil
André V.G. Cavalieri
Affiliation:
Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP 12228-900, Brazil
André F.C. da Silva
Affiliation:
Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP 12228-900, Brazil
William R. Wolf
Affiliation:
Faculdade de Engenharia Mecânica, Universidade Estadual de Campinas, Campinas, SP 12228-900, Brazil
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

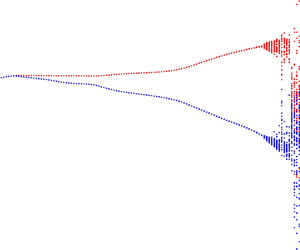
We present the results of direct numerical simulations of a NACA 0012 airfoil, with Mach number 0.3 and angle of attack of $3^\circ$, examining the dynamics of the flow with increasing Reynolds numbers. Two-dimensional simulation results are obtained with chord-based Reynolds numbers in the range $3.2 \times 10^3 \leq Re \leq 2.70 \times 10^4$, where each simulation uses the last time step of the previous one as a starting point, to capture the evolution of dynamics as a function of $Re$. The development of the pressure fluctuations with time shows a transition from periodic to quasi-periodic attractor for $2.38 \times 10^4 \leq Re \leq 2.42 \times 10^4$, leading to the emergence of secondary tones in the wall and acoustic field pressure spectra, different from peaks related to the fundamental frequency $f_1$ and the respective harmonics; a second, incommensurate frequency $f_2$ appears, leading to several secondary tones with frequency $af_1 + bf_2$, with $a$ and $b$ integers. Further increase of the Reynolds number leads to the emergence of a tertiary frequency, $f_3$, indicating a route to chaos of the Ruelle–Takens–Newhouse type. Such a mechanism is related to the ladder-type characteristic structure of the tones, indicating that dynamic systems theory is an important tool for understanding airfoil tonal noise.

JFM classification

Acoustics: Aeroacoustics Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Chaos
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 966 , 10 July 2023 , A8
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abreu, L.I., Cavalieri, A.V.G. & Wolf, W.R. 2017 Coherent hydrodynamic waves and trailing-edge noise. AIAA Paper 2017-3173. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Alligood, K.T., Sauer, T.D. & Yorke, J.A. 1996 Chaos. Springer.CrossRefGoogle Scholar
Arbey, H. & Bataille, J. 1983 Noise generated by airfoil profiles placed in a uniform laminar flow. J. Fluid Mech. 134, 33–47.CrossRefGoogle Scholar
Arcondoulis, E.J.G., Doolan, C.J., Zander, A.C. & Brooks, L.A. 2010 A review of trailing edge noise generated by airfoils at low to moderate Reynolds number. Acoust. Australia 38 (3), 129–133.Google Scholar
Cavalieri, A.V.G., Rempel, E.L. & Nogueira, P.A.S. 2022 Transition to chaos in a reduced-order model of a shear layer. J. Fluid Mech. 932, A43.CrossRefGoogle Scholar
Eckmann, J.P. & Ruelle, D. 1985 Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57 (3), 617.Google Scholar
Ffowcs Williams, J.E. & Hall, L.H. 1970 Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid Mech. 40 (4), 657–670.CrossRefGoogle Scholar
Fosas de Pando, M., Schmid, P.J. & Sipp, D. 2014 A global analysis of tonal noise in flows around aerofoils. J. Fluid Mech. 754, 5–38.CrossRefGoogle Scholar
Golubev, V. 2021 Recent advances in acoustics of transitional airfoils with feedback-loop interactions: a review. Appl. Sci. 11 (3), 1057.CrossRefGoogle Scholar
Guckenheimer, J. & Holmes, P. 2013 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, vol. 42. Springer.Google Scholar
Jaiswal, P., Pasco, Y., Yakhina, G. & Moreau, S. 2022 Experimental investigation of aerofoil tonal noise at low Mach number. J. Fluid Mech. 932, A37.CrossRefGoogle Scholar
Jones, L.E & Sandberg, R.D. 2011 Numerical analysis of tonal airfoil self-noise and acoustic feedback-loops. J. Sound Vib. 330 (25), 6137–6152.CrossRefGoogle Scholar
Jones, L.E, Sandham, N.D. & Sandberg, R.D. 2010 Acoustic source identification for transitional airfoil flows using cross correlations. AIAA J. 48 (10), 2299–2312.CrossRefGoogle Scholar
Kashinath, K., Waugh, I.C. & Juniper, M.P. 2014 Nonlinear self-excited thermoacoustic oscillations of a ducted premixed flame: bifurcations and routes to chaos. J. Fluid Mech. 761, 399–430.CrossRefGoogle Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbits near onset of chaos in plane Couette flow. Chaos 22 (4), 047505.CrossRefGoogle ScholarPubMed
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Longhouse, R.E. 1977 Vortex shedding noise of low tip speed, axial flow fans. J. Sound Vib. 53 (1), 25–46.CrossRefGoogle Scholar
Lustro, J.R.T., Kawahara, G., van Veen, L., Shimizu, M. & Kokubu, H. 2019 The onset of transient turbulence in minimal plane couette flow. J. Fluid Mech. 862, R2.CrossRefGoogle Scholar
Moreau, S. & Roger, M. 2009 Back-scattering correction and further extensions of Amiet's trailing-edge noise model. Part II: application. J. Sound Vib. 323 (1–2), 397–425.CrossRefGoogle Scholar
Nagarajan, S., Lele, S.K. & Ferziger, J.H. 2003 A robust high-order compact method for large eddy simulation. J. Comput. Phys. 191 (2), 392–419.CrossRefGoogle Scholar
Newhouse, S., Ruelle, D. & Takens, F. 1978 Occurrence of strange axiom a attractors near quasi periodic flows on ${T}^m, m \ge 3$. Commun. Math. Phys. 64 (1), 35–40.CrossRefGoogle Scholar
Padois, T., Laffay, P., Idier, A. & Moreau, S. 2016 Tonal noise of a controlled-diffusion airfoil at low angle of attack and Reynolds number. J. Acoust. Soc. Am. 140 (1), EL113–EL118.CrossRefGoogle ScholarPubMed
Paterson, R.W., Vogt, P.G., Fink, M.R. & Munch, C.L. 1973 Vortex noise of isolated airfoils. J. Aircraft 10 (5), 296–302.CrossRefGoogle Scholar
Paul, S., Verma, M.K., Wahi, P., Reddy, S.K. & Kumar, K. 2012 Bifurcation analysis of the flow patterns in two-dimensional Rayleigh–Bénard convection. Intl J. Bifurcation Chaos 22 (05), 1230018.CrossRefGoogle Scholar
Paul, S., Wahi, P. & Verma, M.K. 2011 Bifurcations and chaos in large-prandtl number Rayleigh–Bénard convection. Intl J. Non-Linear Mech. 46 (5), 772–781.CrossRefGoogle Scholar
Pröbsting, S., Scarano, F. & Morris, S.C. 2015 Regimes of tonal noise on an airfoil at moderate Reynolds number. J. Fluid Mech. 780, 407–438.CrossRefGoogle Scholar
Pröbsting, S. & Yarusevych, S. 2015 Laminar separation bubble development on an airfoil emitting tonal noise. J. Fluid Mech. 780, 167–191.CrossRefGoogle Scholar
Ricciardi, T.R., Arias-Ramirez, W. & Wolf, W.R. 2020 On secondary tones arising in trailing-edge noise at moderate Reynolds numbers. Eur. J. Mech. (B/Fluids) 79, 54–66.CrossRefGoogle Scholar
Ricciardi, T.R. & Wolf, W.R. 2022 Switch of tonal noise generation mechanisms in airfoil transitional flows. Phys. Rev. Fluids 7 (8), 084701.CrossRefGoogle Scholar
Ricciardi, T.R., Wolf, W.R. & Taira, K. 2022 Transition, intermittency and phase interference effects in airfoil secondary tones and acoustic feedback loop. J. Fluid Mech. 937, A23.CrossRefGoogle Scholar
Ruelle, D. & Takens, F. 1971 On the nature of turbulence. In Les rencontres physiciens-mathématiciens de Strasbourg-RCP25, vol. 12, pp. 1–44. Available at: http://www.numdam.org/item/RCP25_1971__12__ A2_0/.Google Scholar
Sandham, N.D. & Salgado, A.M. 2008 Nonlinear interaction model of subsonic jet noise. Phil. Trans. R. Soc. A: Math. Phys. Engng Sci. 366 (1876), 2745–2760.CrossRefGoogle ScholarPubMed
Sanjose, M., Towne, A., Jaiswal, P., Moreau, S., Lele, S. & Mann, A. 2019 Modal analysis of the laminar boundary layer instability and tonal noise of an airfoil at Reynolds number 150,000. Intl J. Aeroacoust. 18 (2-3), 317–350.CrossRefGoogle Scholar
Sano, A., Abreu, L.I., Cavalieri, A.V.G. & Wolf, W.R. 2019 Trailing-edge noise from the scattering of spanwise-coherent structures. Phys. Rev. Fluids 4 (9), 094602.CrossRefGoogle Scholar
Suponitsky, V., Sandham, N.D. & Morfey, C.L. 2010 Linear and nonlinear mechanisms of sound radiation by instability waves in subsonic jets. J. Fluid Mech. 658, 509–538.CrossRefGoogle Scholar
Takagi, S. & Konishi, Y. 2010 Frequency selection mechanism of airfoil trailing-edge noise. J. Aircraft 47 (4), 1111–1116.CrossRefGoogle Scholar
Tam, C.K.W. 1974 Discrete tones of isolated airfoils. J. Acoust. Soc. Am. 55 (6), 1173–1177.CrossRefGoogle Scholar
Tam, C.K.W. & Ju, H. 2012 Aerofoil tones at moderate Reynolds number. J. Fluid Mech. 690, 536–570.CrossRefGoogle Scholar
Wolf, W.R., Azevedo, J.L.F. & Lele, S.K. 2012 Convective effects and the role of quadrupole sources for aerofoil aeroacoustics. J. Fluid Mech. 708, 502–538.CrossRefGoogle Scholar
Wolf, W.R., Cavalieri, A.V.G., Backes, B., Morsch-Flho, E. & Azevedo, J.L.F. 2015 Sound and sources of sound in a model problem with wake interaction. AIAA J. 53 (9), 2588–2606.CrossRefGoogle Scholar
Wu, H., Sandberg, R.D. & Moreau, S. 2021 Stability characteristics of different aerofoil flows at $rec= 150,000$ and the implications for aerofoil self-noise. J. Sound Vib. 506, 116152.CrossRefGoogle Scholar
Yakhina, G., Roger, M., Moreau, S., Nguyen, L. & Golubev, V. 2020 Experimental and analytical investigation of the tonal trailing-edge noise radiated by low Reynolds number aerofoils. In Acoustics, vol. 2, pp. 293–329. Multidisciplinary Digital Publishing Institute.CrossRefGoogle Scholar
Yarusevych, S., Sullivan, P.E. & Kawall, J.G. 2006 Coherent structures in an airfoil boundary layer and wake at low Reynolds numbers. Phys. Fluids 18 (4), 044101.CrossRefGoogle Scholar
Zang, B., Mayer, Y. & Azarpeyvand, M. 2019 An experimental investigation on the mechanism of Tollmien-Schlichting waves for a NACA 0012 aerofoil. In 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, AIAA paper 2019-2609. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar