Published online by Cambridge University Press: 07 August 2019
In a recent paper (J. Fluid Mech., vol. 861, 2019, pp. 328–348), Benilov derived equations governing a laminar liquid sheet (a curtain) that emanates from a slot whose centreline is inclined to the vertical. The equations are valid for slender sheets whose characteristic length scale in the direction of flow is much larger than its cross-sectional thickness. For a liquid that leaves a slot with average speed, 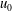 $u_{0}$, volumetric flow rate per unit width,
$u_{0}$, volumetric flow rate per unit width, 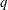 $q$, surface tension,
$q$, surface tension,  $\unicode[STIX]{x1D70E}$, and density,
$\unicode[STIX]{x1D70E}$, and density, 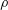 $\unicode[STIX]{x1D70C}$, Benilov obtains parametric equations that predict steady-state curtain shapes that bend upwards against gravity provided
$\unicode[STIX]{x1D70C}$, Benilov obtains parametric equations that predict steady-state curtain shapes that bend upwards against gravity provided 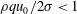 $\unicode[STIX]{x1D70C}qu_{0}/2\unicode[STIX]{x1D70E}<1$. Benilov’s parametric equations are shown to be identical to those derived by Finnicum, Weinstein, and Ruschak (J. Fluid Mech., vol. 255, 1993, pp. 647–665). In the latter form, it is straightforward to deduce an alternative solution of Benilov’s equations where a curtain falls vertically regardless of the slot’s orientation. This solution is consistent with prior experimental and theoretical results that show that a liquid curtain can emerge from a slot at an angle different from that of the slot centreline.
$\unicode[STIX]{x1D70C}qu_{0}/2\unicode[STIX]{x1D70E}<1$. Benilov’s parametric equations are shown to be identical to those derived by Finnicum, Weinstein, and Ruschak (J. Fluid Mech., vol. 255, 1993, pp. 647–665). In the latter form, it is straightforward to deduce an alternative solution of Benilov’s equations where a curtain falls vertically regardless of the slot’s orientation. This solution is consistent with prior experimental and theoretical results that show that a liquid curtain can emerge from a slot at an angle different from that of the slot centreline.