Published online by Cambridge University Press: 17 December 2019
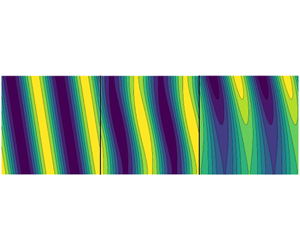
We study the term in the eddy energy budget of continuously stratified quasigeostrophic turbulence that is responsible for energy extraction by eddies from the background mean flow. This term is a quadratic form, and we derive Euler–Lagrange equations describing its eigenfunctions and eigenvalues, the former being orthogonal in the energy inner product and the latter being real. The eigenvalues correspond to the instantaneous energy growth rate of the associated eigenfunction. We find analytical solutions in the Eady problem. We formulate a spectral method for computing eigenfunctions and eigenvalues, and compute solutions in Phillips-type and Charney-type problems. In all problems, instantaneous growth is possible at all horizontal scales in both inviscid problems and in problems with linear Ekman friction. We conjecture that transient growth at small scales is matched by linear transfer to decaying modes with the same horizontal structure, and we provide simulations supporting the plausibility of this hypothesis. In Charney-type problems, where the linear problem has exponentially growing modes at small scales, we expect net energy extraction from the mean flow to be unavoidable, with an associated nonlinear transfer of energy to dissipation.