Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alfredsson, P.H.
Imayama, S.
Lingwood, R.J.
Örlü, R.
and
Segalini, A.
2013.
Turbulent boundary layers over flat plates and rotating disks—The legacy of von Kármán: A Stockholm perspective.
European Journal of Mechanics - B/Fluids,
Vol. 40,
Issue. ,
p.
17.
Carroll, Nick J.
Jensen, Kaare H.
Parsa, Shima
Holbrook, N. Michele
and
Weitz, David A.
2014.
Measurement of Flow Velocity and Inference of Liquid Viscosity in a Microfluidic Channel by Fluorescence Photobleaching.
Langmuir,
Vol. 30,
Issue. 16,
p.
4868.
Trip, Renzo
and
Fransson, Jens H. M.
2014.
Boundary layer modification by means of wall suction and the effect on the wake behind a rectangular forebody.
Physics of Fluids,
Vol. 26,
Issue. 12,
Pouransari, Zeinab
Vervisch, Luc
and
Johansson, Arne V.
2014.
Reynolds Number Effects on Statistics and Structure of an Isothermal Reacting Turbulent Wall-Jet.
Flow, Turbulence and Combustion,
Vol. 92,
Issue. 4,
p.
931.
Bailey, S. C. C.
Vallikivi, M.
Hultmark, M.
and
Smits, A. J.
2014.
Estimating the value of von Kármán’s constant in turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
79.
Pouransari, Z.
Biferale, L.
and
Johansson, A. V.
2015.
Statistical analysis of the velocity and scalar fields in reacting turbulent wall-jets.
Physics of Fluids,
Vol. 27,
Issue. 2,
Segalini, Antonio
Rüedi, Jean-Daniel
and
Monkewitz, Peter A.
2015.
Systematic errors of skin-friction measurements by oil-film interferometry.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
298.
Vallikivi, M.
Hultmark, M.
and
Smits, A. J.
2015.
Turbulent boundary layer statistics at very high Reynolds number.
Journal of Fluid Mechanics,
Vol. 779,
Issue. ,
p.
371.
Titchener, Neil
Colliss, Simon
and
Babinsky, Holger
2015.
On the calculation of boundary-layer parameters from discrete data.
Experiments in Fluids,
Vol. 56,
Issue. 8,
Örlü, Ramis
Segalini, Antonio
Klewicki, Joseph
and
Alfredsson, P. Henrik
2016.
High-order generalisation of the diagnostic scaling for turbulent boundary layers.
Journal of Turbulence,
Vol. 17,
Issue. 7,
p.
664.
Zanoun, E.-S.
Öngüner, E.
and
Egbers, C.
2016.
Conventional measuring probes in the wall layer of turbulent subsonic ducted flows.
Thermophysics and Aeromechanics,
Vol. 23,
Issue. 3,
p.
329.
Vinuesa, Ricardo
Duncan, Richard D.
and
Nagib, Hassan M.
2016.
Alternative interpretation of the Superpipe data and motivation for CICLoPE: The effect of a decreasing viscous length scale.
European Journal of Mechanics - B/Fluids,
Vol. 58,
Issue. ,
p.
109.
Vinuesa, Ricardo
and
Nagib, Hassan M.
2016.
Enhancing the accuracy of measurement techniques in high Reynolds number turbulent boundary layers for more representative comparison to their canonical representations.
European Journal of Mechanics - B/Fluids,
Vol. 55,
Issue. ,
p.
300.
Baars, W. J.
Squire, D. T.
Talluru, K. M.
Abbassi, M. R.
Hutchins, N.
and
Marusic, I.
2016.
Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element.
Experiments in Fluids,
Vol. 57,
Issue. 5,
Belle, A.
Brandner, P.A.
Pearce, B.W.
de Graaf, K.L.
and
Clarke, D.B.
2016.
Artificial thickening and thinning of cavitation tunnel boundary layers.
Experimental Thermal and Fluid Science,
Vol. 78,
Issue. ,
p.
75.
Sanmiguel Vila, C.
Vinuesa, R.
Discetti, S.
Ianiro, A.
Schlatter, P.
and
Örlü, R.
2017.
On the identification of well-behaved turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
p.
109.
Grossmann, Siegfried
and
Lohse, Detlef
2017.
Curvature effects on the velocity profile in turbulent pipe flow.
The European Physical Journal E,
Vol. 40,
Issue. 2,
Örlü, R.
Fiorini, T.
Segalini, A.
Bellani, G.
Talamelli, A.
and
Alfredsson, P. H.
2017.
Reynolds stress scaling in pipe flow turbulence—first results from CICLoPE.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 375,
Issue. 2089,
p.
20160187.
Bobke, A.
Vinuesa, R.
Örlü, R.
and
Schlatter, P.
2017.
History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
667.
Wadhwani, Rahul
Sutherland, Duncan
Ooi, Andrew
Moinuddin, Khalid
and
Thorpe, Graham
2017.
Verification of a Lagrangian particle model for short-range firebrand transport.
Fire Safety Journal,
Vol. 91,
Issue. ,
p.
776.
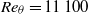 ${\mathit{Re}}_{\theta } = 11\hspace{0.167em} 100$ to 67 000. Only small differences were found amongst commonly used corrections for velocity shear, but improvements were found for existing near-wall proximity corrections. Corrections for the nonlinear averaging of the velocity fluctuations were also investigated, and the results compared to hot-wire data taken as part of the same measurement campaign. The streamwise turbulence-intensity correction was found to be of comparable magnitude to that of the shear correction, and found to bring the hot-wire and Pitot results into closer agreement when applied to the data, along with the other corrections discussed and refined here.
${\mathit{Re}}_{\theta } = 11\hspace{0.167em} 100$ to 67 000. Only small differences were found amongst commonly used corrections for velocity shear, but improvements were found for existing near-wall proximity corrections. Corrections for the nonlinear averaging of the velocity fluctuations were also investigated, and the results compared to hot-wire data taken as part of the same measurement campaign. The streamwise turbulence-intensity correction was found to be of comparable magnitude to that of the shear correction, and found to bring the hot-wire and Pitot results into closer agreement when applied to the data, along with the other corrections discussed and refined here.