Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T17:00:11.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of cavitation regimes in flow over a circular cylinder

Published online by Cambridge University Press:  23 December 2019

Filipe L. Brandao ,
Mrugank Bhatt  and
Krishnan Mahesh Open the ORCID record for Krishnan Mahesh [Opens in a new window]
Filipe L. Brandao
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Mrugank Bhatt
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Cavitating flow over a circular cylinder is investigated over a range of cavitation numbers ($\unicode[STIX]{x1D70E}=5$ to $0.5$) for both laminar (at Reynolds number $(Re)=200$) and turbulent (at $Re=3900$) regimes. We observe non-cavitating, cyclic and transitional cavitation regimes with reduction in free-stream $\unicode[STIX]{x1D70E}$. The cavitation inside the Kármán vortices in the cyclic regime, is significantly altered by the onset of ‘condensation front’ propagation in the transitional regime. At the transition, an order of magnitude jump in shedding Strouhal number ($St$) is observed as the dominant frequency shifts from periodic vortex shedding in the cyclic regime, to irregular–regular vortex shedding in the transitional regime. In addition, a peak in pressure fluctuations, and a maximum in $St$ versus $\unicode[STIX]{x1D70E}$ based on cavity length are observed at the transition. Shedding characteristics in each regime are discussed using dynamic mode decomposition. A numerical method based on the homogeneous mixture model, fully compressible formulation and finite rate mass transfer developed by Gnanaskandan & Mahesh (Intl J. Multiphase Flow, vol. 70, 2015, pp. 22–34) is extended to include the effects of non-condensable gas (NCG). It is demonstrated that the condensation fronts observed in the transitional regime are supersonic (referred to as ‘condensation shocks’). In the presence of NCG, multiple condensation shocks in a given cycle are required for complete cavity condensation and detachment, as compared to a single condensation shock when only vapour is present. This is explained by the reduction in pressure ratio across the shock in the presence of NCG, effectively reducing its strength. In addition, at $\unicode[STIX]{x1D70E}=0.85$ (near transition from the cyclic to the transitional regime), the presence of NCG suppresses the low frequency irregular–regular vortex shedding. Vorticity transport at $Re=3900$, in the transitional regime, indicates that the region of attached cavity is nearly two-dimensional, with very low vorticity, affecting Kármán shedding in the near wake. Majority of vortex stretching/tilting and vorticity production is observed following the cavity trailing edge. In addition, the boundary-layer separation point is found to be strongly dependent on the amounts of vapour and gas in the free stream for both laminar and turbulent regimes.

JFM classification

Drops and Bubbles: Cavitation Multiphase and Particle-laden Flows: Multiphase flow Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A19
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharamu, S. & Mahesh, K. 2019 A parallel and streaming dynamic mode decomposition algorithm with finite precision error analysis for large data. J. Comput. Phys. 380, 355–377.CrossRefGoogle Scholar
Arakeri, V. H. 1975 Viscous effects on the position of cavitation separation from smooth bodies. J. Fluid Mech. 68, 779–799.CrossRefGoogle Scholar
Beattie, D. R. H. & Whalley, P. B. 1982 Simple two-phase fractional pressure drop calculation method. Intl J. Multiphase Flow 8, 83–87.CrossRefGoogle Scholar
Bhatt, M. & Mahesh, K. 2018 Investigation of sheet to cloud transition due to the propagation of condensation fronts over a sharp wedge using large eddy simulations. In Proceedings of the 10th International Symposium on Cavitation. ASME.Google Scholar
Brandao, F., Bhatt, M. & Mahesh, K. 2018 Effects of non-condensable gas on cavitating flow over a cylinder. In Proceedings of the 10th International Symposium on Cavitation. ASME.Google Scholar
Briancon-Marjollet, L., Franc, J. P. & Michel, J. M. 1990 Transient bubbles interacting with an attached cavity and the boundary layer. J. Fluid Mech. 218, 355–376.CrossRefGoogle Scholar
Budich, B., Schmidt, S. & Adams, N. A. 2018 Numerical simulation and analysis of condensation shocks in cavitating flows. J. Fluid Mech. 838, 759–813.CrossRefGoogle Scholar
Campbell, I. J. & Pitcher, A. S. 1958 Shock waves in liquid containing gas bubbles. Proc. R. Soc. Lond. A 243 (1235), 534–545.Google Scholar
Chen, J. L., Xue, B., Mahesh, K. & Siepmann, J. I. 2019 Molecular simulations probing the thermophysical properties of homogeneously stretched and bubbly water systems. J. Chem. Engng Data 64 (9), 3755–3771.CrossRefGoogle Scholar
Durgin, W. W. & Karlsson, S. K. F. 1971 On the phenomenon of vortex street breakdown. J. Fluid Mech. 48, 507–527.CrossRefGoogle Scholar
Franc, J. P. & Michel, J. M. 2005 Fundamentals of Cavitation. Kluwer Academic.Google Scholar
Fry, S. A. 1984 Investigating cavity/wake dynamics for a circular cylinder by measuring noise spectra. J. Fluid Mech. 142, 187–200.CrossRefGoogle Scholar
Ganesh, H., Deijlen, L., Bhatt, A., Wu, J. & Ceccio, S. L. 2018 Cavitation dynamics in wakes of bluff bodies. In 32nd Symposium on Naval Hydrodyanmics.Google Scholar
Ganesh, H., Makiharju, S. A. & Ceccio, S. L. 2016 Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. J. Fluid Mech. 802, 37–78.CrossRefGoogle Scholar
Gnanaskandan, A. & Mahesh, K. 2015 A numerical method to simulate turbulent cavitating flows. Intl J. Multiphase Flow 70, 22–34.CrossRefGoogle Scholar
Gnanaskandan, A. & Mahesh, K. 2016a Large eddy simulation of the transition from sheet to cloud cavitation over a wedge. Intl J. Multiphase Flow 83, 86–102.CrossRefGoogle Scholar
Gnanaskandan, A. & Mahesh, K. 2016b Numerical investigation of near-wake characteristics of cavitating flow over a circular cylinder. J. Fluid Mech. 790, 453–491.CrossRefGoogle Scholar
Holl, J. W., Billet, M. L. & Weir, D. S. 1975 Thermodynamic effects on developed cavitation. J. Fluids Engng 97 (4).CrossRefGoogle Scholar
Hsiao, C.-T. & Chahine, G. L. 2005 Scaling of tip vortex cavitation inception noise with a bubble dynamics model accounting for nuclei size distribution. Trans. ASME-I-J. Fluids Engng 127 (1).CrossRefGoogle Scholar
Jahangir, S., Hogendoorn, W. & Poelma, C. 2018 Dyanmics of partial cavitation in an axisymmetric converging-diverging nozzle. Intl J. Multiphase Flow 106, 34–45.CrossRefGoogle Scholar
Jakobsen, J. K. 1964 On the mechanism of head breakdown in cavitating inducers. J. Basic Engng 86 (2), 291–305.CrossRefGoogle Scholar
Ji, B., Luo, X., Peng, X., Zhang, Y., Wu, Y. & Xu, H. 2010 Numerical investigation of the ventilated cavitating flow around an under-water vehicle based on a three-component cavitation model. J. Hydrodyn. 22 (6), 753–759.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2019 Transition to the secondary vortex street in the wake of a circular cylinder. J. Fluid Mech. 867, 691–722.CrossRefGoogle Scholar
Karasudani, T. & Funakoshi, M. 1994 Evolution of a vortex street in the far wake of a cylinder. Fluid Dyn. Res. 14, 331–352.CrossRefGoogle Scholar
Karplus, H. B. 1957 Velocity of sound in a liquid containing gas bubbles. J. Acoust. Soc. Am. 29, 12–61.CrossRefGoogle Scholar
Kawakami, D. T., Gin, Q. & Arndt, R. 2005 Water quality and the periodicity of sheet/cloud cavitation. In Proceedings of FEDSM’05.Google Scholar
Kieffer, S. W. 1977 Sound speed in liquid–gas mixtures: water–air and water–steam. J. Geophys. Res. 82, 2895–2904.CrossRefGoogle Scholar
Kumar, P., Bakshi, S. & Chatterjee, D. 2017a Experimental investigation of cavitation behind a circular cylinder in cross-flow. J. Therm. Sci. Engng Appl. 9, 0310004.Google Scholar
Kumar, P., Chatterjee, D. & Bakshi, S. 2017b Experimental investigation of cavitating structures in the near wake of a cylinder. Intl J. Multiphase Flow 89, 207–217.CrossRefGoogle Scholar
Kunz, R., Boger, F., Stinebring, D. R., Chyczewski, T. S., Lindau, J. W., Gibeling, H. J., Venkateswaran, S. & Govindan, T. R. 2000 A preconditioned Navier–Stokes method for two-phase flows with application to cavitation. Comput. Fluids 29 (8), 849–875.CrossRefGoogle Scholar
Laberteaux, K. R. & Ceccio, S. L. 2001 Partial cavity flows. Part 1. Cavities forming on models without spanwise variation. J. Fluid Mech. 431, 1–41.CrossRefGoogle Scholar
Lagumbay, R. S.2006 Modeling and simulation of multiphase/multicomponent flows. PhD thesis, University of Colorado.Google Scholar
Lu, N. X., Bark, G. & Bensow, R. 2012 Introducing non-condensable gas in unsteady sheet cavitation modelling. In 15th Numerical Towing Tank Symposium.Google Scholar
Makiharju, S. A., Ganesh, H. & Ceccio, S. L. 2017 The dynamics of partial cavity formation, shedding and the influence of dissolved and injected non-condensable gas. J. Fluid Mech. 829, 420–458.CrossRefGoogle Scholar
Mithun, M. G., Koukouvinis, P. & Gavaises, M. 2018 Numerical simulation of cavitation and atomization using a fully compressible three-phase model. Phys. Rev. Fluids 3 (6), 064304.CrossRefGoogle Scholar
Orley, F., Trummler, T., Hickel, S., Mihatsch, M. S., Schmidt, S. J. & Adams, N. A. 2015 Large-eddy simulation of cavitating nozzle flow and primary jet break-up. Phys. Fluids 27, 086101.CrossRefGoogle Scholar
Park, N. & Mahesh, K.2007 Numerical and modeling issues in LES of compressible turbulence on unstructed grids. AIAA Paper 2007-722.CrossRefGoogle Scholar
Ramamurthy, A. S. & Bhaskaran, P. 1977 Constrained flow past cavitating bluff bodies. J. Fluids Engng 99 (4), 717–726.CrossRefGoogle Scholar
Rao, B. C. S. & Chandrasekhara, D. V. 1976 Some characteristics of cavity flow past cylindrical inducers in venturi. J. Fluids Engng 98 (3), 461–466.Google Scholar
Saito, Y., Takami, R., Nakamori, I. & Ikohagi, T. 2007 Numerical analysis of unsteady behavior of cloud cavitation around a NACA0015 foil. Comput. Mech. 40, 85–96.CrossRefGoogle Scholar
Schenke, S. & van Terwisga, T. J. C. 2017 Simulating compressibility in cavitating flow using incompressible mass transfer solver. In 5th International Symposium of Marine Propulsors.Google Scholar
Seo, J. H., Moon, Y. J. & Shin, B. R. 2008 Prediction of cavitation flow noise by direct numerical simulation. J. Comput. Phys. 227, 6511–6531.CrossRefGoogle Scholar
Singhal, A. K., Athavale, M. M., Li, H. & Jiang, Y. 2002 Mathematical basis and validation of the full cavitation model. J. Fluids Engng 124, 617–624.CrossRefGoogle Scholar
Toro, E. F. 1999 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer.CrossRefGoogle Scholar
Trummler, T., Freytag, L., Schmidt, S. J. & Adams, N. A. 2018 Large eddy simulation of a collapsing vapor bubble containing non-condensable gas. In Proceedings of the 10th International Symposium on Cavitation. ASME.Google Scholar
Varga, J. & Sebestiyen, G. 1965 Experimental investigation of some properties of cavitating flow. Period. Polytech. 9 (3), 243–254.Google Scholar
Vennig, J., Smith, S., Brandner, P., Giosio, D. & Pearce, B. 2017 The influence of nuclei content on cloud cavitation about a hydrofoil. In International Symposium on Transport Phenomena and Dynamics of Rotating Machinery.Google Scholar
White, F. M. 2006 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Wu, X., Maheux, E. & Chahine, G. L. 2017 An experimental study on sheet to cloud cavitation. Exp. Therm. Fluid Sci. 83, 129–140.CrossRefGoogle Scholar
Yee, H. C., Sandham, N. D. & Djomehri, M. J. 1999 Low-dissipative high-order shock-capturing methods using characteristic-based filters. J. Comput. Phys. 150 (1), 199–238.CrossRefGoogle Scholar
Young, J. O. & Holl, J. W. 1966 Effects of cavitation on periodic wakes behind symmetric wedges. J. Basic Engng 88 (1), 163–176.CrossRefGoogle Scholar

Brandao et al. supplementary movie 1

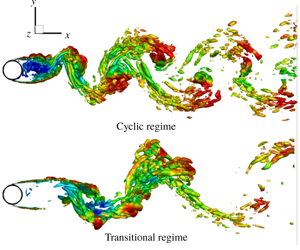
Fig 5(a). Instantaneous total void fraction contour for the cyclic regime for Case B.

Download Brandao et al. supplementary movie 1(Video)
Video 174.4 KB

Brandao et al. supplementary movie 2

Fig 5(b,c). Instantaneous total void fraction contour for the transitional regime for Case B.

Download Brandao et al. supplementary movie 2(Video)
Video 511.5 KB
Supplementary material: File

Brandao et al. supplementary figure 1

Figure_1: Vapor volume fraction fluctuation for Case A200 at sigma=1.

Download Brandao et al. supplementary figure 1(File)
File 306.7 KB
Supplementary material: File

Brandao et al. supplementary figure 2

Figure_2: NCG volume fraction fluctuation for Case A200 at sigma=1.

Download Brandao et al. supplementary figure 2(File)
File 261.2 KB
Supplementary material: File

Brandao et al. supplementary figure 3

Figure_3: Average local cavitation number for Case A200 at sigma=1.

Download Brandao et al. supplementary figure 3(File)
File 310.8 KB
Supplementary material: File

Brandao et al. supplementary figure 4

Figure_4: Average velocity magnitude for Case A200 at sigma=1.

Download Brandao et al. supplementary figure 4(File)
File 837.3 KB
Supplementary material: File

Brandao et al. supplementary figure 5

Figure_5: Vapor volume fraction fluctuation for Case A200 at sigma=0.7.

Download Brandao et al. supplementary figure 5(File)
File 392.7 KB
Supplementary material: File

Brandao et al. supplementary figure 6

Figure_6: NCG volume fraction fluctuation for Case A200 at sigma=0.7.

Download Brandao et al. supplementary figure 6(File)
File 253.2 KB
Supplementary material: File

Brandao et al. supplementary figure 7

Figure_7: Average local cavitation number for Case A200 at sigma=0.7.

Download Brandao et al. supplementary figure 7(File)
File 877.2 KB
Supplementary material: File

Brandao et al. supplementary figure 8

Figure_8: Average velocity magnitude for Case A200 at sigma=0.7.

Download Brandao et al. supplementary figure 8(File)
File 877.2 KB