Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T03:10:22.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of laminar–turbulent transition in laminar separation bubbles: the effect of free-stream turbulence

Published online by Cambridge University Press:  12 November 2018

Shirzad Hosseinverdi Open the ORCID record for Shirzad Hosseinverdi [Opens in a new window]  and
Hermann F. Fasel
Shirzad Hosseinverdi*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
Hermann F. Fasel
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The role of free-stream turbulence (FST) in the hydrodynamic instability mechanisms and transition to turbulence in laminar separation bubbles (LSBs) was investigated using direct numerical simulations (DNS). Towards this end, a set of highly resolved DNS have been carried out, where isotropic FST fluctuations with intensities from 0.1 % to 3 % are introduced to investigate the relevant physical mechanisms governing the interaction of separation and transition in LSBs. For disturbance-free simulations, i.e. without FST, laminar–turbulent transition involves a Kelvin–Helmholtz (KH) instability of the separated shear layer. For LSBs subjected to FST, vortical FST fluctuations penetrate the approaching attached laminar boundary layer upstream of the separation location and induce slowly growing low-frequency disturbances, so-called Klebanoff (K) modes, which cause a spanwise modulation with a distinct spanwise wavelength. Simultaneously, the FST enhances the initial levels of instability waves with frequencies in the frequency range of the KH instability, but at much smaller amplitude levels compared to the K-modes. Results from the calculations based on the linearized Navier–Stokes equations and comparison with DNS results reveal that the K-mode exhibits exponential growth in the separated shear layer until it reaches a peak amplitude. At the same time, two-dimensional (2D) disturbance waves are also exponentially amplified, in fact at larger growth rate compared to the K-mode, due to the primary (convective) shear-layer instability mechanism until they saturate downstream of the peak amplitude associated with the K-mode. Therefore, based on detailed spectral analysis and modal decompositions for the separation bubbles investigated, the transition process is the result of two different mechanisms: (i) strong amplification of high-frequency (order of the shedding frequency), essentially 2D or weakly oblique fluctuating disturbances and (ii) low-frequency, three-dimensional K-modes caused by FST. Depending on the intensity of the FST, one of these mechanisms would dominate the transition process, or both mechanisms act together and contribute simultaneously. The net effect of these two events is an acceleration of transition for an increased level of FST intensity, which in turn leads to a reduction of the extent of the separation bubble in streamwise and wall-normal directions. The ‘roll-up’ into spanwise large-scale vortical structures resulting from the shear-layer instability, and the eventual breakdown of these structures, strongly contribute to the reattachment process. The spanwise coherence of these ‘rollers’ deteriorates due to the presence of large-amplitude K-modes, thus effectively weakening their strength for high levels of FST intensities (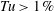$Tu>1\,\%$).

JFM classification

Boundary Layers: Boundary layer separation Instability: Instability Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 714 - 759
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abu-Ghannam, B. J. & Shaw, R. 1980 Natural transition of boundary layers the effects of turbulence, pressure gradient, and flow history. J. Mech. Engng Sci. 22 (5), 213–228.Google Scholar
Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.Google Scholar
Balzer, W. & Fasel, H. F. 2016 Numerical investigation of the role of free-stream turbulence in boundary-layer separation. J. Fluid Mech. 801, 289–321.Google Scholar
Boiko, A. V., Grek, G. R., Dovgal, A. V. & Kozlov, V. V. 2002 The Origin of Turbulence in Near-wall Flows, 1st edn. Springer.Google Scholar
Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.Google Scholar
Brinkerhoff, J. R. & Yaras, M. I. 2015 Numerical investigation of transition in a boundary layer subjected to favourable and adverse streamwise pressure gradients and elevated free stream turbulence. J. Fluid Mech. 781, 52–86.Google Scholar
Burgmann, S. & Schröder, W. 2008 Investigation of the vortex induced unsteadiness of a separation bubble via time-resolved and scanning PIV measurements. Exp. Fluids 45, 675–691.Google Scholar
Chetan, S. J. & Fasel, H. F.2012 Experimental investigation of the structure and dynamics of laminar separation bubbles. In 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA Paper 2012-755. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Diwan, S. S., Chetan, S. J. & Ramesh, O. N. 2006 On the bursting criterion for laminar separation bubbles. In IUTAM Symposium on Laminar–Turbulent Transition, pp. 401–407. Springer.Google Scholar
Diwan, S. S. & Ramesh, O. N. 2009 On the origin of the inflectional instability of a laminar separation bubble. J. Fluid Mech. 629, 263–298.Google Scholar
Dovgal, A. V., Kozlov, V. V. & Michalke, A. 1994 Laminar boundary layer separation: instability and associated phenomena. Prog. Aerosp. Sci. 30 (1), 61–94.Google Scholar
Embacher, M. & Fasel, H. F. 2014 Direct numerical simulations of laminar separation bubbles: investigation of absolute instability and active flow control of transition to turbulence. J. Fluid Mech. 747, 141–185.Google Scholar
Fasel, H. F. 2002 Numerical investigation of the interaction of the Klebanoff-mode with a Tollmien–Schlichting wave. J. Fluid Mech. 450, 1–33.Google Scholar
Gaster, M.1969 The structure and behaviour of laminar separation bubbles. ARC Reports and Memoranda 3595. Aeronautical Research Council (ARC).Google Scholar
Gaster, M. & Grant, I. 1975 An experimental investigation of the formation and development of a wave packet in a laminar boundary layer. Proc. R. Soc. Lond. A 347 (1649), 253–269.Google Scholar
Goldstein, M. E. 2014 Effect of free-stream turbulence on boundary layer transition. Phil. Trans. R. Soc. Lond. A 372 (2020), 1–18.Google Scholar
Greenblatt, D. & Wygnanski, I. J. 2000 The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 36 (7), 487–545.Google Scholar
Grosch, C. E. & Salwen, H. 1978 The continuous spectrum of the Orr–Sommerfeld equation. Part 1. The spectrum and the eigenfunctions. J. Fluid Mech. 87 (1), 33–54.Google Scholar
Häggmark, C.2000 Investigations of disturbances developing in a laminar separation bubble flow. PhD thesis, KTH, Department of Mechanics, Stockholm.Google Scholar
Hammond, D. A. & Redekopp, L. G. 1998 Local and global instability properties of separation bubbles. Eur. J. Mech. (B/Fluids) 17 (2), 145–164.Google Scholar
Horton, H. P.1968 Laminar separation in two and three-dimensional incompressible flow. PhD thesis, University of London.Google Scholar
Hosseinverdi, S., Balzer, W. & Fasel, H. F.2012 Direct numerical simulations of the effect of free-stream turbulence on ‘long’ laminar separation bubbles. In 42nd AIAA Fluid Dynamics Conference and Exhibit, AIAA Paper 2012-2972. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Hosseinverdi, S. & Fasel, H. F.2013a Direct numerical simulations of transition to turbulence in two-dimensional laminar separation bubbles. In 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA Paper 2013-264. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Hosseinverdi, S. & Fasel, H. F.2013b Numerical investigation of the effect of free-stream turbulence on separation control by pulsed vortex generator jets. In 43rd Fluid Dynamics Conference, AIAA Paper 2013-2614. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Hosseinverdi, S. & Fasel, H. F.2016 Direct numerical simulations of laminar-to-turbulent transition in laminar separation bubbles in three-dimensional boundary-layer. In 46th AIAA Fluid Dynamics Conference, AIAA Paper 2016-3793. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Hosseinverdi, S. & Fasel, H. F. 2018 Role of Klebanoff modes in active flow control of separation: direct numerical simulations. J. Fluid Mech. 850, 954–983.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.Google Scholar
Hunt, J. C. R., Durbin, P. A., Kevlahan, N. K. R. & Fernando, H. J. S. 1996 Non-local effects of shear in turbulent flows. In Sixth European Turbulence Conference, Lausanne, Switzerland, Springer.Google Scholar
Jacobs, R. G. & Durbin, P. A. 1998 Shear sheltering and the continuous spectrum of the Orr–Sommerfeld equation. Phys. Fluids 10 (8), 2006–2011.Google Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulations of bypass transition. J. Fluid Mech. 428, 185–212.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jones, L. E., Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulations of forced and unforced separation bubbles on an airfoil at incidence. J. Fluid Mech. 602, 175–207.Google Scholar
Kendall, J. M.1985 Experimental study of disturbances produced in a pretransitional laminar boundary layer by weak freestream turbulence. In 18th Fluid Dynamics and Plasma Dynamics and Lasers Conference, AIAA Paper 1985-1695. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Kendall, J. M.1990 Boundary layer receptivity to freestream turbulence. In 21st Fluid Dynamics, Plasma Dynamics and Lasers Conference, AIAA Paper 1990-1504 American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Klebanoff, P. S. 1971 Effect of free-stream turbulence on a laminar boundary layer. Bull. Am. Phys. Soc. 16 (11), 1323.Google Scholar
Klebanoff, P. S. & Tidstrom, K. D.1959 Evolution of amplified waves leading to transition in a boundary layer with zero pressure gradient. Tech. Note D-195. NASA.Google Scholar
Landahl, M. T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28 (4), 735–756.Google Scholar
Lardeau, S., Leschziner, M. & Zaki, T. 2012 Large eddy simulation of transitional separated flow over a flat plate and a compressor blade. Flow Turbul. Combust. 88 (1), 19–44.Google Scholar
Leib, S. J., Wundrow, D. W. & Goldstein, M. E. 1999 Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 380, 169–203.Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–178. Nauka.Google Scholar
Marxen, O. & Henningson, D. S. 2011 The effect of small-amplitude convective disturbances on the size and bursting of a laminar separation bubble. J. Fluid Mech. 671, 1–33.Google Scholar
Marxen, O., Lang, M., Rist, U., Levin, O. & Henningson, D. S. 2009 Mechanisms for spatial steady three-dimensional disturbance growth in a non-parallel and separating boundary layer. J. Fluid Mech. 634, 165–189.Google Scholar
Marxen, O., Lang, M., Rist, U. & Wagner, S. 2003 A combined experimental/numerical study of unsteady phenomena in a laminar separation bubble. Flow Turbul. Combust. 71 (1), 133–146.Google Scholar
Marxen, O., Rist, U. & Wagner, S. 2004 Effect of spanwise-modulated disturbances on transition in a separated boundary layer. AIAA J. 42 (5), 937–944.Google Scholar
Matsubara, M. & Alfredsson, P. H. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.Google Scholar
McAuliffe, B. R. & Yaras, M. I. 2010 Transition mechanisms in separation bubbles under low-and elevated-freestream turbulence. Trans. ASME J. Turbomach. 132 (1), 11004–11010.Google Scholar
Meitz, H. L. & Fasel, H. F. 2000 A compact-difference scheme for the Navier–Stokes equations in vorticity–velocity formulation. J. Comput. Phys. 157 (1), 371–403.Google Scholar
Michelis, T., Yarusevych, S. & Kotsonis, M. 2017 Response of a laminar separation bubble to impulsive forcing. J. Fluid Mech. 820, 633–666.Google Scholar
Morkovin, M. V. 1969 On the many faces of transition. In Viscous Drag Reduction (ed. Sinclair Wells, C.), pp. 1–31. Springer.Google Scholar
Moser, R. D. & Moin, P. 1987 The effects of curvature in wall-bounded turbulent flows. J. Fluid Mech. 175, 479–510.Google Scholar
Na, Y. & Moin, P. 1998 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 370, 175–201.Google Scholar
Olson, D. A., Katz, A. W., Naguib, A. M., Koochesfahani, M. M., Rizzetta, D. P. & Visbal, M. R. 2013 On the challenges in experimental characterization of flow separation over airfoils at low Reynolds number. Exp. Fluids 54 (2), 1470.Google Scholar
Ossia, S. & Lesieur, M. 2001 Large-scale energy and pressure dynamics in decaying 2D incompressible isotropic turbulence. J. Turbul. 2 (13), 1–34.Google Scholar
Owen, P. R. & Klanfer, L.1953 On the laminar boundary layer separation from the leading edge of a thin aerofoil. ARC C.P. 220. Aeronautical Research Council (ARC).Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Postl, D., Balzer, W. & Fasel, H. F. 2011 Control of laminar separation using pulsed vortex generator jets: direct numerical simulations. J. Fluid Mech. 676, 81–109.Google Scholar
Radi, A. & Fasel, H. F.2010 Experimental investigation of laminar separation bubbles on a flat plate. In 40th Fluid Dynamics Conference and Exhibit, AIAA Paper 2010-4482. American Institute of Aeronautics and Astronautics (AIAA).Google Scholar
Rao, V. N., Tucker, P. G., Jefferson-Loveday, R. J. & Coull, J. D. 2013 Large eddy simulations in low-pressure turbines: effect of wakes at elevated free-stream turbulence. Intl J. Heat Fluid Flow 43, 85–95.Google Scholar
Rist, U. 2003 Instability and transition mechanisms in laminar separation bubbles. In VKI/RTO-LS Low Reynolds Number Aerodynamics on Aircraft Including Applications in Emerging UAV Technology, pp. 1–29. von Karman Institute.Google Scholar
Rist, U. & Maucher, U. 2002 Investigations of time-growing instabilities in laminar separation bubbles. Eur. J. Mech. (B/Fluids) 21 (5), 495–509.Google Scholar
Rodríguez, D., Gennaro, E. M. & Juniper, M. P. 2013 The two classes of primary modal instability in laminar separation bubbles. J. Fluid Mech. 734, R4.Google Scholar
Rodríguez, D. & Theofilis, V. 2010 Structural changes of laminar separation bubbles induced by global linear instability. J. Fluid Mech. 655, 280–305.Google Scholar
Satta, F., Simoni, D., Ubaldi, M., Zunino, P., Bertini, F. & Spano, E. 2007 Velocity and turbulence measurements in a separating boundary layer with and without passive flow control. IMechE A: J. Power Energy 221 (6), 815–818.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schubauer, G. B. & Skramstad, H. K.1948 Laminar-boundary-layer oscillations and transition on a flat plate. NACA Tech. Rep. 909. National Advisory Committee for Aeronautics.Google Scholar
Simoni, D., Lengani, D., Ubaldi, M., Zunino, P. & Dellacasagrande, M. 2017 Inspection of the dynamic properties of laminar separation bubbles: free-stream turbulence intensity effects for different Reynolds numbers. Exp. Fluids 58 (66), 1–14.Google Scholar
Simoni, D., Ubaldi, M. & Zunino, P. 2014 Experimental investigation of flow instabilities in a laminar separation bubble. J. Therm. Sci. 23 (3), 203–214.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Spalart, P. R. & Strelets, M. K. 2000 Mechanisms of transition and heat transfer in a separation bubble. J. Fluid Mech. 403, 329–349.Google Scholar
von Terzi, D. A.2004 Numerical investigation of transitional and turbulent backward-facing step flows. PhD thesis, The University of Arizona.Google Scholar
Watmuff, J. H. 1999 Evolution of a wave packet into vortex loops in a laminar separation bubble. J. Fluid Mech. 397, 119–169.Google Scholar
Westin, K. J. A., Boiko, A. V., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subjected to free stream turbulence. Part 1. Boundary layer structure and receptivity. J. Fluid Mech. 281, 193–218.Google Scholar
Wissink, J. G. & Rodi, W. 2006 Direct numerical simulations of transitional flow in turbomachinery. Trans. ASME J. Turbomach. 128 (4), 668–678.Google Scholar
Yarusevych, S., Kawall, J. G. & Sullivan, P. E. 2006 Airfoil performance at low Reynolds numbers in the presence of periodic disturbances. J. Fluids Engng 128 (3), 587–595.Google Scholar
Zaki, T. A. & Durbin, P. A. 2006 Continuous mode transition and the effects of pressure gradient. J. Fluid Mech. 563, 357–388.Google Scholar
Zaki, T. A., Wissink, J. G., Rodi, W. & Durbin, P. A. 2010 Direct numerical simulations of transition in a compressor cascade: the influence of free-stream turbulence. J. Fluid Mech. 665, 57–98.Google Scholar