Article contents
Numerical investigation of a jet from a blunt body opposing a supersonic flow
Published online by Cambridge University Press: 30 August 2011
Abstract
Numerical investigation of a sonic jet from a blunt body opposing a supersonic flow with a free stream Mach number 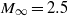 was carried out using large-eddy simulation for two total pressure ratios of the jet to the free stream, i.e.
was carried out using large-eddy simulation for two total pressure ratios of the jet to the free stream, i.e. 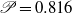 and 1.633. Results have been validated carefully against experimental data. Various fundamental mechanisms dictating the flow phenomena, including shock/jet interaction, shock/shear-layer interaction, turbulent shear-layer evolution and coherent structures, have been studied systematically. Based on the analysis of the flow structures and features, two typical flow states, i.e. unstable and stable states corresponding to the two values of
and 1.633. Results have been validated carefully against experimental data. Various fundamental mechanisms dictating the flow phenomena, including shock/jet interaction, shock/shear-layer interaction, turbulent shear-layer evolution and coherent structures, have been studied systematically. Based on the analysis of the flow structures and features, two typical flow states, i.e. unstable and stable states corresponding to the two values of  , are identified and the behaviours relevant to the flow states are discussed. Small-scale vortical structures mainly occur in the jet column, and large-scale vortices develop gradually in a recirculation region when the jet terminates through a Mach disk and reverses its orientation as a conical free shear layer. The turbulent fluctuations are enhanced by the rapid deviation of the shear layer and the interaction with shock waves. Moreover, the coherent structures of the flow motion are analysed using the proper orthogonal decomposition technique. It is found that the dominant mode in the cross-section plane exhibits an antisymmetric character for the unstable state and an axisymmetric one for the stable state, while statistical analysis of unsteady loads indicates that the side loads can be seen as a rotating vector uniformly distributed in the azimuthal direction. Further, we clarify a feedback mechanism whereby the unsteady motion is sustained by the upstream-propagating disturbance to the Mach disk through the recirculation subsonic region and downstream propagation in the conical shear layer. Feedback models are then proposed which can reasonably well predict the dominant frequencies of the two flow states. The results obtained in this study provide physical insight into the understanding of the mechanisms relevant to the opposing jet/supersonic flow interaction.
, are identified and the behaviours relevant to the flow states are discussed. Small-scale vortical structures mainly occur in the jet column, and large-scale vortices develop gradually in a recirculation region when the jet terminates through a Mach disk and reverses its orientation as a conical free shear layer. The turbulent fluctuations are enhanced by the rapid deviation of the shear layer and the interaction with shock waves. Moreover, the coherent structures of the flow motion are analysed using the proper orthogonal decomposition technique. It is found that the dominant mode in the cross-section plane exhibits an antisymmetric character for the unstable state and an axisymmetric one for the stable state, while statistical analysis of unsteady loads indicates that the side loads can be seen as a rotating vector uniformly distributed in the azimuthal direction. Further, we clarify a feedback mechanism whereby the unsteady motion is sustained by the upstream-propagating disturbance to the Mach disk through the recirculation subsonic region and downstream propagation in the conical shear layer. Feedback models are then proposed which can reasonably well predict the dominant frequencies of the two flow states. The results obtained in this study provide physical insight into the understanding of the mechanisms relevant to the opposing jet/supersonic flow interaction.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 85
- Cited by


