Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T14:41:29.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical and experimental investigation of oblique shock wave reflection off a water wedge

Published online by Cambridge University Press:  10 August 2017

Q. Wan ,
H. Jeon ,
R. Deiterding  and
V. Eliasson Open the ORCID record for V. Eliasson [Opens in a new window]
Q. Wan
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089-1189, USA
H. Jeon
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089-1189, USA
R. Deiterding
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
V. Eliasson*
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089-1189, USA Department of Structural Engineering, University of California, San Diego, La Jolla, CA 92093-0085, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Shock wave interaction with solid wedges has been an area of much research in past decades, but so far very few results have been obtained for shock wave reflection off liquid wedges. In this study, numerical simulations are performed using the inviscid Euler equations and the stiffened gas equation of state to study the transition angles, reflection patterns and triple point trajectory angles of shock reflection off solid and water wedges. Experiments using an inclined shock tube are also performed and schlieren photography results are compared to simulations. Results show that the transition angles for the water wedge cases are within 5.3 % and 9.2 %, for simulations and experiments respectively, compared to results obtained with the theoretical detachment criterion for solid surfaces. 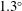Triple point trajectory angles are measured and compared with analytic solutions, agreement within $1.3^{\circ }$ is shown for the water wedge cases. The transmitted wave in the water observed in the simulation is quantitatively studied, and two different scenarios are found. For low incident shock Mach numbers, 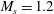$M_{s}=1.2$ and 2, no shock wave is formed in the water but a precursor wave is induced ahead of the incident shock wave and passes the information from the water back into the air. For high incident shock Mach numbers, 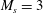$M_{s}=3$ and 4, precursor waves no longer appear but instead a shock wave is formed in the water and attached to the Mach stem at every instant. The temperature field in the water is measured in the simulation. For strong incident shock waves, e.g. 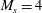$M_{s}=4$, the temperature increment in the water is up to 7.3 K.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Gas dynamics Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 732 - 758
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abgrall, R. & Karni, S. 2001 Computations of compressible multifluids. J. Comput. Phys. 169, 594–623.CrossRefGoogle Scholar
Baskar, S., Coulouvrat, F. & Marchiano, R. 2007 Nonlinear reflection of grazing acoustic shock waves: unsteady transition from von Neumann to Mach to Snell–Descartes reflections. J. Fluid Mech. 575, 27–55.Google Scholar
Ben-Dor, G.1978 Regions and transitions of non-stationary oblique shock wave diffractions in perfect and imperfect gases. UTIAS Rep. 232.Google Scholar
Ben-Dor, G. 1980 Analytical solution of double-Mach reflection. AIAA J. 18 (9), 1036–1043.CrossRefGoogle Scholar
Ben-Dor, G. 1981 Relation between first and second triple-point trajectory angles in double-Mach reflection. AIAA J. 19 (4), 531–533.CrossRefGoogle Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena. Springer.Google Scholar
Ben-Dor, G. & Glass, I. I. 1979 Domains and boundaries of non-stationary oblique shock-wave reflexions. 1. Diatomic gas. J. Fluid Mech. 92, 459–496.Google Scholar
Ben-Dor, G. & Glass, I. I. 1980 Domains and boundaries of non-stationary oblique shock-wave reflexions. 2. Monatomic gas. J. Fluid Mech. 96, 735–756.Google Scholar
Ben-Dor, G., Mazor, G., Takayama, K. & Igra, O. 1987 Influence of surface roughness on the transition from regular to Mach reflection in pseudo-steady flows. J. Fluid Mech. 176, 333–356.CrossRefGoogle Scholar
Ben-Dor, G. & Takayama, K. 1992 The phenomena of shock wave reflection – a review of unsolved problems and future research needs. Shock Waves 2, 211–223.Google Scholar
Birkhoff, G. 1950 Hydrodynamics, A Study in Logic, Fact and Similitude. Princeton University Press.Google Scholar
Bleakney, W., Weimer, D. K. & Fletcher, C. H. 1949 The shock tube: a facility for investigations in fluid dynamics. Rev. Sci. Instrum. 20, 807–815.Google Scholar
Borisov, A. A., Kogarko, S. M. & Lyubimov, A. V. 1965 Sliding of detonation and shock waves over liquid surfaces. Combust. Explos. Shock Waves 1, 19–23.Google Scholar
Cirak, F., Deiterding, R. & Mauch, S. P. 2007 Large-scale fluid–structure interaction simulation of viscoplastic and fracturing thin shells subjected to shocks and detonations. Comput. Struct. 85, 1049–1065.CrossRefGoogle Scholar
Cole, R. H. 1948 Underwater Explosions. Dover.Google Scholar
Colella, P. & Henderson, L. F. 1990 The von Neumann paradox for the diffraction of weak shock waves. J. Fluid Mech. 213, 71–94.Google Scholar
Deiterding, R. 2009 A parallel adaptive method for simulating shock-induced combustion with detailed chemical kinetics in complex domains. Comput. Struct. 87, 769–783.Google Scholar
Deiterding, R. 2011 Block-structured adaptive mesh refinement-theory, implementation and application. ESAIM: Proc. 34, 97–150.CrossRefGoogle Scholar
Deiterding, R., Cirak, F. & Mauch, S. P. 2009 Efficient fluid–structure interaction simulation of viscoplastic and fracturing thin-shells subjected to underwater shock loading. In International Workshop on Fluid-Structure Interaction (ed. Hartmann, S., Meister, A., Schäfer, M. & Turek, S.), Theory, Numerics and Applications, Herrsching am Ammersee, pp. 65–80. Kassel University Press GmbH.Google Scholar
Deiterding, R., Radovitzky, R., Mauch, S. P., Noels, L., Cummings, J. C. & Meiron, D. I. 2006 A virtual test facility for the efficient simulation of solid material response under strong shock and detonation wave loading. Engng Comput. 22 (3–4), 325–347.Google Scholar
Delpino Gonzales, O. & Eliasson, V. 2015 Effect of water content on dynamic fracture. Initiation of vinyl ester. Exp. Mech. 56, 637–644.Google Scholar
Desjouy, C., Ollivier, S., Marsden, O., Karzova, M. & Blanc-Benon, P. 2016 Irregular reflection of weak acoustic shock pulses on rigid boundaries: schlieren experiments and direct numerical simulation based on a Navier–Stokes solver. Phys. Fluids. 28, 027102.Google Scholar
Flåtten, T., Morin, A. & Munkefjord, S. T. 2011 On solutions to equilibrium problems for systems of stiffened gases. SIAM J. Appl. Maths 71 (1), 41–67.Google Scholar
Fox, R. W., McDonald, A. T. & Pritchard, P. J. 1985 Introduction to Fluid Mechanics. Wiley.Google Scholar
Geva, M., Ram, O. & Sadot, O. 2013 The non-stationary hysteresis phenomenon in shock wave reflections. J. Fluid Mech. 732, R1.Google Scholar
Grove, J. W. & Menikoff, R. 1990 Anomalous reflection of a shock wave at a fluid interface. J. Fluid Mech. 219, 313–336.CrossRefGoogle Scholar
Henderson, L. F., Ma, J., Sakurai, A. & Takayama, K. 1990 Refraction of a shock wave at an air–water interface. Fluid Dyn. Res. 5, 337–350.Google Scholar
Hornung, H. G., Oertel, H. & Sandeman, R. J. 1979 Transition to Mach reflexion of shock waves in steady and pseudosteady flow with and without relaxation. J. Fluid Mech. 90, 541–560.Google Scholar
Hornung, H. G. & Robinson, M. L. 1982 Transition from regular to Mach reflection of shock waves. Part 2. The steady-flow criterion. J. Fluid Mech. 123, 155–164.Google Scholar
Hornung, H. G. & Taylor, J. R. 1982 Transition from regular to Mach reflection of shock waves. Part 1. The effect of viscosity in the pseudo-steady case. J. Fluid Mech. 123, 143–153.CrossRefGoogle Scholar
Igra, D. & Takayama, K. 2001 Numerical simulation of shock wave interaction with a water column. Shock Waves 11, 219–228.Google Scholar
Igra, D. & Takayama, K. 2001 Investigation of aerodynamic breakup of a cylindrical water droplet. Atomiz. Sprays 11, 167–185.Google Scholar
Jeon, H., Gross, J. R., Estabrook, S., Koumlis, S., Wan, Q., Khanolkar, G. R., Tao, X., Mensching, D. M., Lesnick, E. J. & Eliasson, V. 2015 Shock wave attenuation using foam obstacles: does geometry matter? Aerosp. 2, 353–375.CrossRefGoogle Scholar
Jolgam, S., Ballil, A., Nowakowski, A. & Nicolleau, F. 2012 On equations of state for simulations of multiphase flows. In Proceedings of the World Congress on Engineering, vol. III. International Association of Engineers.Google Scholar
Karzova, M. M., Khokhlova, V. A., Salze, E., Ollivier, S. & Blanc-Benon, P. 2015 Mach stem formation in reflection and focusing of weak shock acoustic pulses. J. Acoust. Soc. Am. 137, EL436–EL442.Google Scholar
Kedrinskii, V. K. 2005 Hydrodynamics of Explosion: Experiments and Models. Springer.Google Scholar
Kleine, H., Timofeev, E., Hakkaki-Fard, A. & Sadot, O. 2014 The influence of Reynolds number on the triple point trajectories at shock reflection off cylindrical surfaces. J. Fluid Mech. 740, 47–60.CrossRefGoogle Scholar
Law, C. K.1970 Diffraction of strong shock waves by a sharp compressive corner. UTIAS Tech. Note 150.Google Scholar
LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
Li, H. & Ben-Dor, G. 1995 Reconsideration of pseudo-steady shock wave reflections and the transition criteria between them. Shock Waves 5, 59–73.CrossRefGoogle Scholar
Mach, E. 1878 Über den Verlauf von Funkenwellen in der Ebene und im Räume. Sitz.ber. Akad. Wiss. Wien 78, 819–838.Google Scholar
Marchiano, R., Coulouvrat, F., Baskar, S. & Thomas, J. L. 2007 Experimental evidence of deviation from mirror reflection for acoustical shock waves. Phys. Rev. E 76, 056602.Google Scholar
Meng, J. C. & Colonius, T. 2015 Numerical simulation of the early stages of high-speed droplet breakup. Shock Waves 25, 399–414.Google Scholar
Mouton, C. A.2006 Transition between regular reflection and Mach reflection in the dual-solution domain. PhD thesis, California Institute of Technology.Google Scholar
Naidoo, K. & Skews, B. W. 2011 Dynamic effects on the transition between two-dimensional regular and Mach reflection of shock waves in an ideal, steady supersonic free stream. J. Fluid Mech. 676, 432–460.CrossRefGoogle Scholar
von Neumann, J.1943a Oblique reflection of shocks. Explos. Res. Rep. 12, Navy Dept., Bureau of Ordinance, Washington, DC, USA.Google Scholar
von Neumann, J.1943b Refraction, intersection and reflection of shock waves. NAVORD Rep. 203–45, Navy Dept., Bureau of Ordinance, Washington, DC, USA.Google Scholar
Onodera, H. & Takayama, K. 1990 Interaction of a plane shock wave with slitted wedges. Exp. Fluids 10, 109–115.Google Scholar
Perotti, L. E., Deiterding, R., Inaba, K., Shepherd, J. & Ortiz, M. 2013 Elastic response of water-filled fiber composite tubes under shock wave loading. Intl J. Solids Struct. 50, 473–486.Google Scholar
Ram, O., Geva, M. & Sadot, O. 2015 High spatial and temporal resolution study of shock wave reflection over a coupled convex–concave cylindrical surface. J. Fluid Mech. 768, 219–239.Google Scholar
Ridah, S. 1988 Shock waves in water. J. Appl. Phys. 64, 152–158.Google Scholar
Rodriguez, V., Jourdan, G., Marty, A., Allou, A. & Parisse, J. D. 2016 Planar shock wave sliding over a water layer. Exp. Fluids 57 (8), 125.Google Scholar
Sakurai, A. 1974 Blast wave from a plane source at an interface. J. Phys. Soc. Japan 36, 610–610.Google Scholar
Sasoh, A., Takayama, K. & Saito, T. 1992 A weak shock wave reflection over wedges. Shock Waves 2, 277–281.CrossRefGoogle Scholar
Saurel, R. & Abgrall, R. 1999 A multiphase Godunov method for compressible multifluid and multiphase flows. J. Comput. Phys. 150, 425–467.Google Scholar
Settles, G. S. 2012 Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media. Springer.Google Scholar
Shyue, K.-M. 1998 An efficient shock-capturing algorithm for compressible multicomponent problems. J. Comput. Phys. 142, 208–242.Google Scholar
Shyue, K.-M. 1999 A fluid-mixture type algorithm for compressible multicomponent flow with van der Waals equation of state. J. Comput. Phys. 156, 43–88.Google Scholar
Shyue, K.-M. 2006 A volume-fraction based algorithm for hybrid barotropic and non-barotropic two-fluid flow problems. Shock Waves 15, 407–423.Google Scholar
Skews, B. 2005 Shock wave interaction with porous plates. Exp. Fluids 39, 875–884.CrossRefGoogle Scholar
Skews, B. W. & Blitterswijk, A. 2011 Shock wave reflection off coupled surfaces. Shock Waves 21, 491–498.Google Scholar
Skews, B. W. & Kleine, H. 2010 Shock wave interaction with convex circular cylindrical surfaces. J. Fluid Mech. 654, 195–205.Google Scholar
Soni, V., Hadjadj, A., Chaudhuri, A. & Ben-Dor, G. 2017 Shock-wave reflections over double-concave cylindrical reflectors. J. Fluid Mech. 813, 70–84.Google Scholar
Takayama, K. & Ben-Dor, G. 1989 Pseudo-steady oblique shock wave reflections over water wedges. Exp. Fluids 8, 129–136.Google Scholar
Teodorczyk, A. & Shepherd, J. E.2012 Interaction of a shock wave with a water layer. Tech. Rep. FM2012-002. Graduate Aeronautical Laboratories, California Institute of Technology.Google Scholar
Toro, E. F., Spruce, M. & Speares, W. 1994 Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 4, 25–34.Google Scholar
Versluis, M. 2013 High-speed imaging in fluids. Exp. Fluids 54, 1458.Google Scholar
Wang, C. & Eliasson, V. 2012 Shock wave focusing in water inside convergent structures. Intl J. Multiphys. 6, 267–282.Google Scholar