Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T05:08:55.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the appearance of wave-packets in steady-state triple-deck solutions of supersonic flow past a compression corner

Published online by Cambridge University Press:  02 December 2022

D. Exposito Open the ORCID record for D. Exposito [Opens in a new window] ,
S.L. Gai Open the ORCID record for S.L. Gai [Opens in a new window]  and
A.J. Neely Open the ORCID record for A.J. Neely [Opens in a new window]
D. Exposito*
Affiliation:
School of Engineering and Information Technology, University of New South Wales, Canberra, ACT 2612, Australia
S.L. Gai
Affiliation:
School of Engineering and Information Technology, University of New South Wales, Canberra, ACT 2612, Australia
A.J. Neely
Affiliation:
School of Engineering and Information Technology, University of New South Wales, Canberra, ACT 2612, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

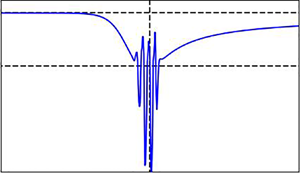
This study is an attempt at solving steady-state triple-deck equations using the method of Bos & Ruban (Phil. Trans. R. Soc. Lond. A, vol. 358, issue 1777, 2000, pp. 3063–3073) for supersonic flow past a compression corner. This was motivated by the fact that in their above paper, they show solutions for scale angles up to 8, the highest obtained so far in the literature. However, we encountered a stationary wave-packet at the corner for scale angles 1.82 and 1.96, depending on the values of stretching factors. Our solutions are then compared with the steady-state solutions produced using the method of Logue, Gajjar & Ruban (Phil. Trans. R. Soc. A, vol. 372, issue 2020, 2014, 20130342), which do not show such wave-packets. These wave-packets do not appear to be the result of flow instability, as flow instabilities should only appear with unsteady equations (Cassel, Ruban & Walker, J. Fluid Mech., vol. 300, 1995, pp. 265–285). It is therefore suggested that the method of Bos & Ruban (Phil. Trans. R. Soc. Lond. A, vol. 358, issue 1777, 2000, pp. 3063–3073) produces these spurious wave-packets as a consequence of their numerical method. This has important implications in the interpretation of triple-deck solutions.

JFM classification

Boundary Layers: Boundary layer separation Compressible Flows: Supersonic flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A8
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bos, S.H. & Ruban, A.I. 2000 A semi–direct method for calculating flows with viscous–inviscid interaction. Phil. Trans. R. Soc. Lond. A 358 (1777), 3063–3073.Google Scholar
Brown, S.N., Cheng, H.K. & Lee, C.J. 1990 Inviscid–viscous interaction on triple-deck scales in a hypersonic flow with strong wall cooling. J. Fluid Mech. 220, 309–337.Google Scholar
Brown, S.N., Stewartson, K. & Williams, P.G. 1975 Hypersonic self-induced separation. Phys. Fluids 18 (6), 633–639.CrossRefGoogle Scholar
Burggraf, O.R. 1975 Asymptotic theory of separation and reattachment of a laminar boundary layer on a compression ramp. Tech. Rep. Ohio State University Research Foundation Columbus.Google Scholar
Cassel, K.W., Ruban, A.I. & Walker, J.D.A. 1995 An instability in supersonic boundary-layer flow over a compression ramp. J. Fluid Mech. 300, 265–285.Google Scholar
Cassel, K.W., Ruban, A.I. & Walker, J.D.A. 1996 The influence of wall cooling on hypersonic boundary-layer separation and stability. J. Fluid Mech. 321, 189–216.Google Scholar
Exposito, D. 2022 Steady-state solutions of supersonic triple-deck equations. https://github.com/dieexbr/bos2000semi, retrieved June 1, 2022.Google Scholar
Exposito, D., Gai, S.L. & Neely, A.J. 2021 Wall temperature and bluntness effects on hypersonic laminar separation at a compression corner. J. Fluid Mech. 922, A1.CrossRefGoogle Scholar
Fletcher, A.J.P., Ruban, A.I. & Walker, J.D.A. 2004 Instabilities in supersonic compression ramp flow. J. Fluid Mech. 517, 309–330.CrossRefGoogle Scholar
Korolev, G.L., Gajjar, J.S.B. & Ruban, A.I. 2002 Once again on the supersonic flow separation near a corner. J. Fluid Mech. 463, 173–199.Google Scholar
Logue, R.P. 2008 Stability and bifurcations governed by the triple deck and related equations. PhD thesis, Manchester.Google Scholar
Logue, R.P., Gajjar, J.S.B. & Ruban, A.I. 2014 Instability of supersonic compression ramp flow. Phil. Trans. R. Soc. A 372 (2020), 20130342.Google ScholarPubMed
Messiter, A.F. 1970 Boundary-layer flow near the trailing edge of a flat plate. SIAM J. Appl. Maths 18 (1), 241–257.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Neiland, V.Y. 1969 Theory of laminar boundary layer separation in supersonic flow. Fluid Dyn. 4 (4), 33–35.Google Scholar
Neiland, V.Y. 1970 Asymptotic theory of plane steady supersonic flows with separation zones. Fluid Dyn. 5 (3), 372–381.CrossRefGoogle Scholar
Rizzetta, D.P., Burggraf, O.R. & Jenson, R. 1978 Triple-deck solutions for viscous supersonic and hypersonic flow past corners. J. Fluid Mech. 89 (3), 535–552.CrossRefGoogle Scholar
Ruban, A.I. 1978 Numerical solution of the local asymptotic problem of the unsteady separation of a laminar boundary layer in a supersonic flow. USSR Comput. Maths Math. Phys. 18 (5), 175–187.CrossRefGoogle Scholar
Ruban, A.I. & Gajjar, J.S.B. 2015 Fluid Dynamics: Asymptotic Problems of Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Smith, F.T. 1979 On the non-parallel flow stability of the blasius boundary layer. Proc. R. Soc. Lond. A 366 (1724), 91–109.Google Scholar
Smith, F.T. 1988 a Finite-time break-up can occur in any unsteady interacting boundary layer. Mathematika 35 (2), 256–273.CrossRefGoogle Scholar
Smith, F.T. 1988 b A reversed-flow singularity in interacting boundary layers. Proc. R. Soc. Lond. A 420 (1858), 21–52.Google Scholar
Smith, F.T. & Bodonyi, R.J. 1985 On short-scale inviscid instabilities in flow past surface-mounted obstacles and other non-parallel motions. Aeronaut. J. 89 (886), 205–212.Google Scholar
Smith, F.T. & Khorrami, A.F. 1991 The interactive breakdown in supersonic ramp flow. J. Fluid Mech. 224, 197–215.CrossRefGoogle Scholar
Stewartson, K. 1970 On supersonic laminar boundary layers near convex corners. Proc. R. Soc. Lond. A 319 (1538), 289–305.Google Scholar
Stewartson, K. & Williams, P.G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312 (1509), 181–206.Google Scholar
Tutty, O.R. & Cowley, S.J. 1986 On the stability and the numerical solution of the unsteady interactive boundary-layer equation. J. Fluid Mech. 168, 431–456.CrossRefGoogle Scholar

Exposito et al. Supplementary Movie 1

Shear-stress distribution with the Bos-Ruban Method for scale angle 2 with I = 201, J = 101, a = b = 10.

Download Exposito et al. Supplementary Movie 1(Video)
Video 4.5 MB

Exposito et al. Supplementary Movie 2

Shear-stress distribution with the Bos-Ruban Method for scale angle 3 with I = 201, J = 101, a = b = 10.

Download Exposito et al. Supplementary Movie 2(Video)
Video 4.9 MB