Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T07:20:09.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on optimum propulsion of heaving and pitching airfoils from linear potential theory

Published online by Cambridge University Press:  15 August 2017

R. Fernandez-Feria Open the ORCID record for R. Fernandez-Feria [Opens in a new window]
R. Fernandez-Feria*
Affiliation:
Fluid Mechanics, Universidad de Málaga, Andalucía Tech, Dr Ortiz Ramos s/n, 29071 Málaga, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The conditions that maximize the propulsive efficiency of a heaving and pitching airfoil are analysed using a novel formulation for the thrust force within the linear potential theory. Stemming from the vortical impulse theory, which correctly predicts the decay of the thrust efficiency as the inverse of reduced frequency 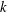$k$ for large 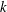$k$ (Fernandez-Feria, Phys. Rev. Fluids, vol. 1, 2016, 084502), the formulation is corrected here at low frequencies by adding a constant representing the viscous drag. It is shown first that the thrust coefficient and propulsive efficiency thus computed agree quite well with several sets of available experimental data, even for not so small flapping amplitudes. For a pure pitching motion, it is found that the maximum propulsion efficiency is reached for the airfoil pitching close to the three-quarter chord point from the leading edge with a relatively large reduced frequency, corresponding to a relatively low thrust coefficient. According to the theory, this efficiency peak may approach unity. For smaller 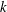$k$, other less pronounced local maxima of the propulsive efficiency are attained for pitching points ahead of the leading edge, with larger thrust coefficients. The linear theory also predicts that no thrust is generated at all for a pitching axis located between the three-quarter chord point and the trailing edge. These findings contrast with the results obtained from the classical linear thrust by Garrick, with the addition of the same quasi-static thrust, which are also computed in the paper. For a combined heaving and pitching motion, the behaviour of the propulsive efficiency in relation to the pitching axis is qualitatively similar to that found for a pure pitching motion, for given fixed values of the feathering parameter (ratio between pitching and heaving amplitudes) and of the phase shift between the pitching and heaving motions. The peak propulsive efficiency predicted by the linear theory is for an airfoil with a pitching axis close to, but ahead of, the three-quarter chord point, with a relatively large reduced frequency, a feathering parameter of approximately 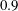$0.9$ and a phase shift slightly smaller than 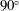$90^{\circ }$.

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 781 - 796
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. M., Streitlien, K., Barret, K. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.CrossRefGoogle Scholar
Baik, Y. S., Bernal, L. P., Granlund, K. & Ol, M. V. 2012 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 709, 37–68.CrossRefGoogle Scholar
Cordes, U., Kampers, G., Meissner, T., Tropea, C., Pinke, J. & Hölling, M. 2017 Note on the limitations of the Theodorsen and Sears functions. J. Fluid Mech. 811, R1.CrossRefGoogle Scholar
Das, A., Shukla, R. K. & Govardhan, R. N. 2016 Existence of a sharp transition in the peak propulsive efficiency of a low-Re pitching foil. J. Fluid Mech. 800, 307–326.CrossRefGoogle Scholar
Fernandez-Feria, R. 2016 Linearized propulsion theory of flapping airfoils revisited. Phys. Rev. Fluids 1, 084502.CrossRefGoogle Scholar
Garrick, I. E.1936 Propulsion of a flapping and oscillating airfoil. NACA Tech. Rep. TR 567.Google Scholar
Garrick, I. E.1938 On some reciprocal relations in the theory of nonstationary flows. NACA Tech. Rep. TR 629.Google Scholar
Heathcote, S. & Gursul, I. 2007 Flexible flapping airfoil propulsion at low Reynolds numbers. AIAA J. 45, 1066–1079.CrossRefGoogle Scholar
Isogai, K., Shinmoto, Y. & Watanabe, Y. 1999 Effects of dynamical stall on propulsive efficiency and thrust of flapping airfoil. AIAA J. 17, 1145–1150.CrossRefGoogle Scholar
Jones, K. D. & Platzer, M. F.1999 An experimental and numerical investigation of flapping-wing propulsion. AIAA Paper 99-0995.CrossRefGoogle Scholar
von Kármán, Th. & Burgers, J. M. 1935 General aerodynamic theory – perfect fluids. In Aerodynamic Theory (ed. Durand, W. F.). Springer.Google Scholar
von Kármán, Th. & Sears, W. R. 1938 Airfoil theory for non-uniform motion. J. Aero. Sci. 5, 370–390.CrossRefGoogle Scholar
Lighthill, M. J. 1969 Hydromechanics of aquatic animal propulsion. Annu. Rev. Fluid Mech. 1, 413–449.CrossRefGoogle Scholar
Lighthill, M. J. 1970 Aquatic animal propulsion of high hydromechanical efficiency. J. Fluid Mech. 44, 265–301.CrossRefGoogle Scholar
Mackowski, A. W. & Williamson, H. K. 2015 Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching. J. Fluid Mech. 765, 524–543.CrossRefGoogle Scholar
Mackowski, A. W. & Williamson, H. K. 2017 Effect of pivot point location and passive heave on propulsion from a pitching airfoil. Phys. Rev. Fluids 2, 013101.CrossRefGoogle Scholar
Platzer, M., Jones, K., Young, J. & Lai, J. 2008 Flapping wing aerodynamics: progress and challenges. AIAA J. 46, 2136–2149.CrossRefGoogle Scholar
Quinn, D. B., Lauder, G. V. & Smits, A. J. 2015 Maximizing the efficiency of a flexible propulsor using experimental optimization. J. Fluid Mech. 767, 430–448.CrossRefGoogle Scholar
Sedov, L. I. 1965 Two-Dimensional Problems in Hydrodynamics and Aerodynamics. Interscience.CrossRefGoogle Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. TR 496.Google Scholar
Tuncer, I. H. & Kaya, M. 2005 Optimization of flapping airfoils for maximum thrust and propulsive efficiency. AIAA J. 43, 2329–2336.CrossRefGoogle Scholar
Wu, T. Y. 1971 Hydromechanics of swimming propulsion. Part 2. Some optimum shape problems. J. Fluid Mech. 46, 521–544.CrossRefGoogle Scholar
Young, J. & Lai, J. C. S. 2007 Mechanisms influencing the efficiency of oscillating airfoil propulsion. AIAA J. 45, 1695–1702.CrossRefGoogle Scholar