Article contents
Nonlinear optimal suppression of vortex shedding from a circular cylinder
Published online by Cambridge University Press: 23 June 2015
Abstract
This study is focused on two- and three-dimensional incompressible flow past a circular cylinder for Reynolds number 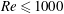 $\mathit{Re}\leqslant 1000$. To gain insight into the mechanisms underlying the suppression of unsteadiness for this flow we determine the nonlinear optimal open-loop control driven by surface-normal wall transpiration. The spanwise-constant wall transpiration is allowed to oscillate in time, although steady forcing is determined to be most effective. At low levels of control cost, defined as the square integration of the control, the sensitivity of unsteadiness with respect to wall transpiration is a good approximation of the optimal control. The distribution of this sensitivity suggests that the optimal control at small magnitude is achieved by applying suction upstream of the upper and lower separation points and blowing at the trailing edge. At high levels of wall transpiration, the assumptions underlying the linearized sensitivity calculation become invalid since the base flow is eventually altered by the size of the control forcing. The large-magnitude optimal control is observed to spread downstream of the separation point and draw the shear layer separation towards the rear of the cylinder through suction, while blowing along the centreline eliminates the recirculation bubble in the wake. We further demonstrate that it is possible to completely suppress vortex shedding in two- and three-dimensional flow past a circular cylinder up to
$\mathit{Re}\leqslant 1000$. To gain insight into the mechanisms underlying the suppression of unsteadiness for this flow we determine the nonlinear optimal open-loop control driven by surface-normal wall transpiration. The spanwise-constant wall transpiration is allowed to oscillate in time, although steady forcing is determined to be most effective. At low levels of control cost, defined as the square integration of the control, the sensitivity of unsteadiness with respect to wall transpiration is a good approximation of the optimal control. The distribution of this sensitivity suggests that the optimal control at small magnitude is achieved by applying suction upstream of the upper and lower separation points and blowing at the trailing edge. At high levels of wall transpiration, the assumptions underlying the linearized sensitivity calculation become invalid since the base flow is eventually altered by the size of the control forcing. The large-magnitude optimal control is observed to spread downstream of the separation point and draw the shear layer separation towards the rear of the cylinder through suction, while blowing along the centreline eliminates the recirculation bubble in the wake. We further demonstrate that it is possible to completely suppress vortex shedding in two- and three-dimensional flow past a circular cylinder up to 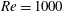 $\mathit{Re}=1000$, accompanied by 70 % drag reduction when a nonlinear optimal control of moderate magnitude (with root-mean-square value 8 % of the free-stream velocity) is applied. This is confirmed through linearized stability analysis about the steady-state solution when the nonlinear optimal wall transpiration is applied. While continuously distributed wall transpiration is not physically realizable, the study highlights localized regions where discrete control strategies could be further developed. It also highlights the appropriate range of application of linear and nonlinear optimal control to this type of flow problem.
$\mathit{Re}=1000$, accompanied by 70 % drag reduction when a nonlinear optimal control of moderate magnitude (with root-mean-square value 8 % of the free-stream velocity) is applied. This is confirmed through linearized stability analysis about the steady-state solution when the nonlinear optimal wall transpiration is applied. While continuously distributed wall transpiration is not physically realizable, the study highlights localized regions where discrete control strategies could be further developed. It also highlights the appropriate range of application of linear and nonlinear optimal control to this type of flow problem.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 32
- Cited by



