Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T01:15:59.199Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear influence of the Earth’s rotation on iceberg melting

Published online by Cambridge University Press:  12 November 2018

Agostino N. Meroni Open the ORCID record for Agostino N. Meroni [Opens in a new window] ,
Craig D. McConnochie Open the ORCID record for Craig D. McConnochie [Opens in a new window] ,
Claudia Cenedese ,
Bruce Sutherland Open the ORCID record for Bruce Sutherland [Opens in a new window]  and
Kate Snow
Agostino N. Meroni*
Affiliation:
Department of Earth and Environmental Sciences, University of Milano-Bicocca, Milan, 20126, Italy
Craig D. McConnochie
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
Claudia Cenedese
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
Bruce Sutherland
Affiliation:
Department of Physics and Department of Earth and Atmospheric Sciences, University of Alberta, Edmonton, T6G 2E3, Canada
Kate Snow
Affiliation:
School of GeoSciences, University of Edinburgh, Edinburgh EH8 9YL, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The calving of icebergs accounts for a significant fraction of the mass loss from both the Antarctic and Greenland ice sheets. Iceberg melting affects the water properties impacting sea ice formation, local circulation and biological activity. Laboratory experiments have investigated the effects of the Earth’s rotation on iceberg melting and the possible formation of Taylor columns (TCs) underneath icebergs. It is found that at high Rossby number, 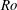$Ro$, when rotation is weak compared to advection, iceberg melting is unaffected by the background rotation. As 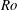$Ro$ decreases, the melt rate shows an increasing trend, which is expected to reverse for very low 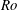$Ro$. This behaviour is explained by considering the integrated horizontal velocity at the base of the iceberg. For moderate 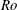$Ro$, a partial TC is formed and its effective blocking accelerates the flow under the remainder of the iceberg, which increases the melt rate since the melting is proportional to the flow velocity. It is expected that for very low 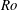$Ro$ the melt rate decreases because, with the expansion of the TC, the region of flow acceleration occurs away from the base of the iceberg. For low free stream velocity the freshwater produced by the ice melting introduces another dynamical effect. It is observed that there is a threshold free stream velocity below which the melt rate is constant. This is explained with the formation of a gravity current at the base of the iceberg that insulates it from the free flow and controls its melting.

JFM classification

Phase change: Phase change Geophysical and Geological Flows: Rotating flows Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 832 - 851
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bigg, G. R. 2015 Icebergs: Their Science and Links to Global Change. Cambridge University Press.Google Scholar
Bigg, G. R., Wadley, M. R., Stevens, D. P. & Johnson, J. A. 1997 Modelling dynamics and thermodynamics of icebergs. Cold Reg. Sci. Technol. 26, 113–135.Google Scholar
Bigg, G. R. & Wilton, D. J. 2014 Iceberg risk in the Titanic year of 1912: was it exceptional? Weather 69 (4), 100–104.Google Scholar
Depoorter, M. A., Bamber, J. L., Griggs, J. A., Lenaerts, J. T. M., Ligtenberg, S. R. M., van den Broeke, M. R. & Moholdt, G. 2013 Calving fluxes and basal melt rates of Antarctic ice shelves. Nature 502 (7469), 89–92.Google Scholar
Duprat, L. P. A., Bigg, G. R. & Wilton, D. J. 2016 Enhanced Southern Ocean marine productivity due to fertilization by giant icebergs. Nat. Geosci. 9, 219–221.Google Scholar
Eckert, E. R. G. & Drake, R. M. 1959 Heat and Mass Transfer. McGraw-Hill.Google Scholar
Enderlin, E. & Howat, I. 2014 An improved mass budget for the Greenland ice sheet. Geophys. Res. Lett. 41, 866–872.Google Scholar
FitzMaurice, A., Cenedese, C. & Straneo, F. 2017 Nonlinear response of iceberg side melting to ocean currents. Geophys. Res. Lett. 44 (11), 5637–5644.Google Scholar
FitzMaurice, A., Cenedese, C. & Straneo, F. 2018 A laboratory study of iceberg side melting in vertically sheared flows. J. Phys. Oceanogr. 48, 1367–1373.Google Scholar
FitzMaurice, A., Straneo, F., Cenedese, C. & Andres, M. 2016 Effect of a sheared flow on iceberg motion and melting. Geophys. Res. Lett. 43, 12520–12527.Google Scholar
Gladstone, R. M., Bigg, G. R. & Nicholls, K. W. 2001 Iceberg trajectory modeling and meltwater injection in the Southern Ocean. J. Geophys. Res. 106, 19903–19915.Google Scholar
Greenslade, M. D. 1994 Strongly stratified airflow over and around mountains. In Stably Stratified Flows: Flow and Dispersion over Topography (ed. Castro, I. P. & Rockcliff, N. J.), pp. 25–37. Clarendon Press.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17 (3), 385–404.Google Scholar
Helly, J. J., Kaufmann, R. S., Stephenson, G. R. & Vernet, M. 2011 Cooling, dilution and mixing of ocean water by free-drifting icebergs in the Weddell Sea. Deep-Sea Res. II 58 (11–12), 1346–1363.Google Scholar
Holland, D. M. & Jenkins, A. 1999 Modeling thermodynamic ice-ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29 (8), 1787–1800.Google Scholar
Huppert, H. E. 1975 Some remarks on the initiation of inertial Taylor columns. J. Fluid Mech. 67 (2), 397–412.Google Scholar
Ingersoll, A. P. 1969 Inertial Taylor columns and Jupiter’s Great Red Spot. J. Atmos. Sci. 26 (4), 744–752.Google Scholar
IOC, SCOR & IAPSO 2010 The International Thermodynamic Equation of Seawater – 2010: Calculation and Use of Thermodynamic Properties, Intergovernmental Oceanographic Commission, Manuals and Guides No. 56. UNESCO.Google Scholar
Johnson, E. R. 1983 Taylor columns in horizontally sheared flow. Geophys. Astrophys. Fluid Dyn. 24, 143–164.Google Scholar
Kader, B. A. & Yaglom, A. M. 1972 Heat and mass transfer laws for fully tubulent wall flows. Intl J. Heat Mass Transfer 15, 2329–2351.Google Scholar
Kerr, R. C. & McConnochie, C. D. 2015 Dissolution of a vertical solid surface by turbulent compositional convection. J. Fluid Mech. 765, 211–228.Google Scholar
King, E. M., Stellmach, S. & Buffet, B. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.Google Scholar
King, E. M., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. M. 2009 Boundary layer control of rotating convection. Nature 457, 301–304.Google Scholar
Rackow, T., Wesche, C., Timmermann, R., Hellmer, H. H., Juricke, S. & Jung, T. 2017 A simulation of small to giant Antarctic iceberg evolution: differential impact on climatology estimates. J. Geophys. Res. Oceans 122, 3170–3190.Google Scholar
Savage, S. B. 2001 Aspects of iceberg deterioration and drift. In LNP 582: Geomorphological Fluid Mechanics (ed. Balmforth, N. J. & Provenzale, A.), pp. 279–318. Springer.Google Scholar
Smith, K. L., Robison, B. H., Helly, J. J., Kaufmann, R. S., Ruhl, H. A., Shaw, T. J., Twining, B. S. & Vernet, M. 2007 Free-drifting icebergs: hot spots of chemical and biological erichment in the Weddell Sea. Science 317 (5837), 478–482.Google Scholar
Stephenson, G. R., Sprintall, J., Gille, S. T., Vernet, M., Helly, J. J. & Kaufmann, R. S. 2015 Subsurface melting of a free-floating Antarctic iceberg. Deep-Sea Res. II 58 (11), 1336–1345.Google Scholar
Stern, A. A., Adcroft, A. & Sergienko, O. 2016 The effects of Antarctic iceberg calving-size distribution in a global climate model. J. Geophys. Res. Oceans 121, 5773–5788.Google Scholar
Stern, A. A., Adcroft, A., Sergienko, O. & Marques, G. 2017 Modeling tabular icebergs submerged in the ocean. J. Adv. Model. Earth Syst. 9 (4), 1948–1972.Google Scholar
Taylor, G. I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. R. Soc. Lond. A 104 (25), 213–220.Google Scholar
Timmermann, R., Wang, Q. & Hellmer, H. H. 2012 Ice-shelf basal melting in a global finite-element sea-ice/ice-shelf/ocean model. Ann. Glaciol. 53 (60), 303–314.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Vreugdenhil, C. A., Gayen, B. & Griffiths, R. W. 2016 Mixing and dissipation in a geostrophic buoyancy-driven circulation. J. Geophys. Res. Oceans 121, 6076–6091.Google Scholar
Wagner, T. J. W., Dell, R. W. & Eisenman, I. 2017 An analytical model of iceberg drift. J. Phys. Oceanogr. 47 (7), 1605–1616.Google Scholar
Weeks, W. F. & Campbell, W. J. 1973 Icebergs as a fresh-water source: an appraisal. J. Glaciol. 12 (65), 207–233.Google Scholar
Wells, A. J. & Worster, M. G. 2008 A geophysical-scale model of vertical natural convection boundary layers. J. Fluid Mech. 609, 111–137.Google Scholar