Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T14:22:37.799Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Boussinesq gravity currents and surface waves generated by lock release in a circular-section channel: theoretical and experimental investigation

Published online by Cambridge University Press:  02 May 2019

L. Chiapponi Open the ORCID record for L. Chiapponi [Opens in a new window] ,
M. Ungarish Open the ORCID record for M. Ungarish [Opens in a new window] ,
D. Petrolo Open the ORCID record for D. Petrolo [Opens in a new window] ,
V. Di Federico Open the ORCID record for V. Di Federico [Opens in a new window]  and
S. Longo Open the ORCID record for S. Longo [Opens in a new window]
L. Chiapponi
Affiliation:
Dipartimento di Ingegneria e Architettura (DIA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
M. Ungarish
Affiliation:
Department of Computer Science, Technion, Israel Institute of Technology, Haifa 32000, Israel
D. Petrolo
Affiliation:
Dipartimento di Ingegneria e Architettura (DIA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
V. Di Federico
Affiliation:
Dipartimento di Ingegneria Civile, Chimica, Ambientale e dei Materiali (DICAM), Università di Bologna, Viale Risorgimento 2, 40136 Bologna, Italy
S. Longo*
Affiliation:
Dipartimento di Ingegneria e Architettura (DIA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a combined theoretical and experimental study of lock-release inertial gravity currents (GCs) propagating in a horizontal channel of circular cross-section with open-top surface in the non-Boussinesq regime. A two-layer shallow-water (SW) model is developed for a generic shape of the cross-section with open top, and then implemented in a finite difference numerical code for the solution in a circular-cross-section channel of the type used in the experiments. The model predicts propagation with (almost) constant speed for a fairly long distance, accompanied by a depression of the ambient free open-top surface behind the front of the current. Sixteen experiments were conducted with a density ratio 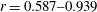$r=0.587{-}0.939$ in full-depth and part-depth release conditions, measuring the front speed and the free-surface time series at four cross-sections. The channel was a circular tube 409 cm long, with a radius of 9.5 cm; the lengths of the locks were 52 and 103.5 cm. Density contrast was obtained by adding sodium chloride and dipotassium phosphate to fresh water. The theoretical values of the front speed and of the depression overestimate the experimental values, but they predict correctly their trend for varying parameters and provide reliable insights into the underlying mechanisms. In particular, we demonstrate that the circular cross-section increases the speed of propagation as compared to the standard rectangular cross-section case (for the same initial height and density ratio). The discrepancies between the SW predictions and the present experiments are of the same order of magnitude as those of previously published results for simpler systems (Boussinesq, rectangular). In addition to the depression, which is a wave bound to, and following the front of, the GC, the system also displays two kinds of free-surface waves, namely the initial bump (its amplitude is of the same order as the depression) and some short-length and low-amplitude waves in the tail of the bump. These free waves propagate with a celerity well predicted by the ‘fast’ eigenvalues of the mathematical model. Comparison is provided with the celerity of a solitary wave. It is expected that discrepancies between theory and experiments can be partly attributed to the presence of these waves. The reported insights and SW prediction method can be applied to a variety of cross-sections of practical interest (triangles, trapezoids, etc.).

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Shallow water flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 610 - 633
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adduce, C., Sciortino, G. & Proietti, S. 2011 Gravity currents produced by lock exchanges: experiments and simulations with a two-layer shallow-water model with entrainment. J. Hydraul. Engng 138 (2), 111–121.Google Scholar
Ancey, C., Cochard, S., Wiederseiner, S. & Rentschler, M. 2006 Front dynamics of supercritical non-Boussinesq gravity currents. Water Resour. Res. 42 (8), W08424.10.1029/2005WR004593Google Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.Google Scholar
Birman, V. K., Martin, J. E. & Meiburg, E. 2005 The non-Boussinesq lock-exchange problem. Part 2. High-resolution simulations. J. Fluid Mech. 537, 125–144.Google Scholar
Bonometti, T., Balachandar, S. & Magnaudet, J. 2008 Wall effects in non-Boussinesq density currents. J. Fluid Mech. 616, 445–475.Google Scholar
Bonometti, T., Ungarish, M. & Balachandar, S. 2011 A numerical investigation of constant-volume non-Boussinesq gravity currents in deep ambient. J. Fluid Mech. 673, 574–602.Google Scholar
Brocchini, M. & Peregrine, D. H. 2001 The dynamics of strong turbulence at free surfaces. Part 1. Description. J. Fluid Mech. 449, 225–254.Google Scholar
Chow, V. T. 1959 Open-Channel Hydraulics. McGraw-Hill.Google Scholar
Dai, A. 2014 Non-Boussinesq gravity currents propagating on different bottom slopes. J. Fluid Mech. 741, 658–680.Google Scholar
Étienne, J., Hopfinger, E. J. & Saramito, P. 2005 Numerical simulations of high density ratio lock-exchange flows. Phys. Fluids 17 (3), 036601.Google Scholar
Gröbelbauer, H. P., Fanneløp, T. K. & Britter, R. E. 1993 The propagation of intrusion fronts of high density ratios. J. Fluid Mech. 250, 669–687.Google Scholar
Haller, M. C. & Tuba Özkan-Haller, H. 2007 Waves on unsteady currents. Phys. Fluids 19 (12), 126601.Google Scholar
Jacobson, M. R. & Testik, F. Y. 2013 On the concentration structure of high-concentration constant-volume fluid mud gravity currents. Phys. Fluids 25 (1), 016602.Google Scholar
La Rocca, M., Adduce, C., Sciortino, G. & Pinzon, A. B. 2008 Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 20 (10), 106603.Google Scholar
Longo, S. 2010 Experiments on turbulence beneath a free surface in a stationary field generated by a crump weir: free-surface characteristics and the relevant scales. Exp. Fluids 49 (6), 1325–1338.Google Scholar
Longo, S., Ungarish, M., Di Federico, V., Chiapponi, L. & Addona, F. 2016 Gravity currents in a linearly stratified ambient fluid created by lock release and influx in semi-circular and rectangular channels. Phys. Fluids 28 (9), 096602.Google Scholar
Longo, S., Ungarish, M., Di Federico, V., Chiapponi, L. & Petrolo, D. 2018 Gravity currents produced by lock-release: theory and experiments concerning the effect of a free top in non-Boussinesq systems. Adv. Water Resour. 121, 456–471.Google Scholar
Lowe, R. J., Rottman, J. W. & Linden, P. F. 2005 The non-Boussinesq lock exchange problem. Part 1. Theory and experiments. J. Fluid Mech. 537, 101–124.Google Scholar
Peregrine, D. H. 1968 Long waves in a uniform channel of arbitrary cross-section. J. Fluid Mech. 32 (2), 353–365.Google Scholar
Robinson, T. O., Eames, I. & Simons, R. 2013 Dense gravity currents moving beneath progressive free-surface water waves. J. Fluid Mech. 725, 588–610.Google Scholar
Rotunno, R., Klemp, J. B., Bryan, G. H. & Muraki, D. J. 2011 Models of non-Boussinesq lock-exchange flow. J. Fluid Mech. 675, 1–26.Google Scholar
Sciortino, G., Adduce, C. & Lombardi, V. 2018 A new front condition for non-Boussinesq gravity currents. J. Hydraul Res. 56 (4), 517–525.Google Scholar
Stancanelli, L. M., Musumeci, R. E. & Foti, E. 2018 Dynamics of gravity currents in the presence of surface waves. J. Geophys. Res. 123 (3), 2254–2273.Google Scholar
Teng, M. H. & Wu, T. Y. 1992 Nonlinear water waves in channels of arbitrary shape. J. Fluid Mech. 242, 211–233.Google Scholar
Turnbull, B. & McElwaine, J. N. 2008 Experiments on the non-Boussinesq flow of self-igniting suspension currents on a steep open slope. J. Geophys. Res. 113, F1.Google Scholar
Ungarish, M. 2007 A shallow-water model for high-Reynolds-number gravity currents for a wide range of density differences and fractional depths. J. Fluid Mech. 579, 373–382.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman & Hall/CRC Press.Google Scholar
Ungarish, M. 2011 Two-layer shallow-water dam-break solutions for non-Boussinesq gravity currents in a wide range of fractional depth. J. Fluid Mech. 675, 27–59.Google Scholar
Ungarish, M. 2017 Benjamin’s gravity current into an ambient fluid with an open surface. J. Fluid Mech. 825, 1–11.Google Scholar
Ungarish, M. 2018 Thin-layer models for gravity currents in channels of general cross-section area, a review. Environ. Fluid Mech. 18 (1), 283–333.Google Scholar
Ungarish, M. 2019 Benjamin’s gravity current into an ambient fluid with an open surface in a channel of general cross-section. J. Fluid Mech. 859, 972–991.Google Scholar
Zemach, T., Chiapponi, L., Petrolo, D., Ungarish, M., Longo, S. & Di Federico, V. 2017 On the propagation of particulate gravity currents in circular and semi-circular channels partially filled with homogeneous or stratified ambient fluid. Phys. Fluids 29 (10), 106605.Google Scholar