Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T00:50:47.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Noise generation mechanisms for a supersonic jet impinging on an inclined plate

Published online by Cambridge University Press:  26 May 2016

Christoph Brehm ,
Jeffrey A. Housman  and
Cetin C. Kiris
Christoph Brehm*
Affiliation:
Science and Technology Corporation, Moffett Field, CA 94035, USA
Jeffrey A. Housman
Affiliation:
Applied Modeling and Simulation Branch, NAS Division, NASA Ames Research Center, Moffett Field, CA 94035, USA
Cetin C. Kiris
Affiliation:
Applied Modeling and Simulation Branch, NAS Division, NASA Ames Research Center, Moffett Field, CA 94035, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Noise generation mechanisms for a perfectly expanded supersonic Mach number 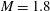$M=1.8$ turbulent jet impinging on a 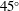$45^{\circ }$ inclined plate are investigated for a Reynolds number of 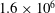$1.6\times 10^{6}$ employing a large-eddy simulation. Excellent comparisons with experimental acoustic far-field measurements and pressure measurements on the impingement plate are obtained. Two local maxima are identified in the far-field overall sound pressure levels in the 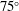$75^{\circ }$ and 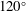$120^{\circ }$ observer directions, which are associated with different noise generation mechanisms. The peak frequencies in the spectra with Strouhal numbers of 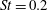$St=0.2$ for 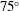$75^{\circ }$ and 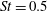$St=0.5$ for 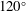$120^{\circ }$ match the experimental measurements. The jet-impingement region generates pressure waves that propagate predominantly in the 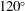$120^{\circ }$ observer direction. The noise generation in this region is attributed to vortex stretching and tearing during shear-layer impingement, and shock oscillations that are induced by the motion of downstream convected vortical flow structures. The second peak in the overall sound pressure distribution at 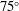$75^{\circ }$ is associated with noise sources located in the wall jet. The noise generation in the wall jet is associated with supersonically convecting large-scale coherent flow structures that also interact with tail shocks in the wall jet causing large localized pressure fluctuations. Strongly coherent flow structures are identified by applying proper orthogonal decomposition (POD) to the unsteady flow field. The frequency characteristics of the most energetic POD modes are distinctly different based on which energy norm is chosen. The most energetic entropy-based POD modes contain a peak frequency of approximately $St=0.4{-}0.6$, while the most energetic turbulent kinetic-energy-based POD modes appear to be dominated by lower-frequency content. The causality method, based on Lighthill’s acoustic analogy, is used to link the acoustic noise signature to the relevant physical mechanisms in the source region. A differentiation is made between the application of normalized and non-normalized cross-correlation functions for noise source identification and characterization.

JFM classification

Acoustics: Aeroacoustics Acoustics: Jet noise Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 797 , 25 June 2016 , pp. 802 - 850
Check for updates
Copyright
© Cambridge University Press 2016. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akamine, M., Nakanishi, Y., Okamoto, K., Teramoto, S., Okunuki, T. & Tsutsumi, S.2014 Experimental study on acoustic phenomena of supersonic jet impinging on inclined flat plate. In 52nd Aerospace Science Meeting. AIAA Paper 2014-0879.Google Scholar
Bogey, C. & Bailly, C.2003 LES of high Reynolds, high subsonic jet: effects of the inflow conditions on flow and noise. AIAA Paper 2003-3170.Google Scholar
Bogey, C. & Bailly, C. 2007 An analysis of the correlations between the turbulent flow and the sound pressure fields of subsonic jets. J. Fluid Mech. 583, 71–97.Google Scholar
Bogey, C., Bailly, C. & Juvé, D. 2003 Noise investigation of a high subsonic, moderate Reynolds number jet using a compressible LES. Theor. Comput. Fluid Dyn. 88 (4), 463–471.Google Scholar
Brehm, C., Barad, M., Housman, J. & Kiris, C. 2015a A comparison of higher-order finite-difference shock capturing schemes. Comput. Fluids 122, 184–208.Google Scholar
Brehm, C. & Fasel, H. F. 2013 A novel concept for the design of immersed interface methods. J. Comput. Phys. 242 (0), 234–267.Google Scholar
Brehm, C., Hader, C. & Fasel, H. F. 2015b A locally stabilized immersed boundary method for the compressible Navier–Stokes equations. J. Comput. Phys. 295, 475–504.Google Scholar
Brehm, C., Housman, J. A., Kiris, C. C. & Hutcheson, F. V.2015c Noise characteristics of a four-jet impingement device inside a broadband engine noise simulator. AIAA Paper 2015-2211.Google Scholar
Brehm, C., Sozer, E., Moini-Yekta, S., Housman, J. A., Barad, M. F., Kiris, C. C., Vu, B. T. & Parlier, C. R.2013 Computational prediction of pressure environment in the flame trench. AIAA Paper 2013-2538.Google Scholar
Brès, G. A., Jaunet, V., Le Rallic, M., Jordan, P., Colonius, T. & Lele, S. K.2015 Large eddy simulation for jet noise: the importance of getting the boundary layer right. AIAA Paper 2015-2535.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78 (7), 808–817.Google Scholar
Clarkson, B. L.1994 Review of sonic fatigue technology. NASA Tech. Memorandum NASA-CR-4587.Google Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.Google Scholar
Dahl, M. D. & Papamoschou, D. 2000 Analytical predictions and measurements of the noise radiated from supersonic coaxial jets. AIAA J. 38 (4), 584–591.Google Scholar
Dauptain, A., Gicquel, L. Y. M. & Moreau, S. 2012 Large eddy simulation of supersonic impinging jets. AIAA J. 50, 1560–1574.Google Scholar
Donea, J. 1984 A Taylor–Galerkin mehtod for convective transport problems. Intl J. Numer. Meth. Engng 20, 101–119.Google Scholar
Dowling, A. P. & Ffowcs Williams, J. E. 1983 Sound and Sources of Sound. Horwood.Google Scholar
Eldred, K.1971 Acoustic loads generated by the propulsion system. Tech. Rep. NASA SP-8072.Google Scholar
Fidkowski, K. J. & Roe, P. L. 2010 An entropy adjoint approach to mesh refinement. SIAM J. Sci. Comput. 32 (3), 1261–1287.CrossRefGoogle Scholar
Freund, J. B. 2001 Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 438, 277–305.CrossRefGoogle Scholar
Freund, J. B. & Colonius, T.2002 Pod analysis of sound generation by a turbulent jet. AIAA Paper 2002-0072.Google Scholar
Ginzburg, I.-P., Semiletenko, V. N. & Uskov, V. N. 1970 Some singularities of supersonic jet interaction with a plane obstacle. Inzh.-Fiz. Zh. 19 (3), 412–417 (translation).Google Scholar
Goldstein, M. E. 1975 The low frequency sound from multipole sources in axisymmetric shear flows, with applications to jet noise. J. Fluid Mech. 70 (03), 595–604.Google Scholar
Goldstein, M. E. 1982 High frequency sound emission from moving point multipole sources embedded in arbitrary transversely sheared mean flows. J. Sound Vib. 80 (4), 499–522.Google Scholar
Haynes, J. & Kenny, R. J. 2009 Modifications to the NASA SP-8072 distributed source method II for Ares I lift-off environment predictions. AIAA Paper 3160.Google Scholar
Henderson, B. 2002 The connection between sound production and jet structure of supersonic impinging jet. J. Acoust. Soc. Am. 111, 735–747.Google Scholar
Henderson, B., Bridges, J. & Wernet, M. 2005 An experimental study of the oscillatory flow structure of tone-producing supersonic impining jets. J. Fluid. Mech. 542, 115–137.Google Scholar
Henderson, B. & Powell, A. 1993 Experiments concerning tones produced by an axisymmetric choked jet impinging on flat plates. J. Sound Vib. 168 (2), 307–326.Google Scholar
Hileman, J. I. & Samimy, M. 2001 Turbulence structures and the acoustic far field of a Mach 1.3 jet. AIAA J. 39 (9), 1716–1727.Google Scholar
Hileman, J. I., Thurow, B. S., Caraballo, E. J. & Samimy, M. 2005 Large-scale structure evolution and sound emission in high-speed jets: real-time visualization with simultaneous acoustic measurements. J. Fluid Mech. 544, 277–307.CrossRefGoogle Scholar
Ho, C.-M. & Nosseir, N. S. 1981 Dynamics of an impinging jet. Part 1. The feedback phenomena. J. Fluid Mech. 105, 119–142.Google Scholar
Honda, H., Nonomura, T., Fujii, K. & Yamamoto, M.2011 Effects of plate angles on acoustic waves from a supersonic jet impinging on an inclined flat plate. AIAA Paper 2011-3260.CrossRefGoogle Scholar
Housman, J. A., Brehm, C. & Kiris, C. C. 2013 Towards jet acoustic prediction within the launch ascent and vehicle aerodynamics framework. J. Acoust. Soc. Am. 134, 4057.Google Scholar
Howe, M. S. 2003 Theory of Vortex Sound, vol. 33. Cambridge University Press.Google Scholar
Hu, X. Y. & Adams, N. A. 2011 Scale separation for implicit large eddy simulation. J. Comput. Phys. 230 (19), 7240–7249.Google Scholar
Hu, X. Y., Wang, Q. & Adams, N. A. 2010 An adaptive central-upwind weighted essentially non-oscillatory scheme. J. Comput. Phys. 229 (23), 8952–8965.CrossRefGoogle Scholar
Hurdle, P. M., Meecham, W. C. & Hodder, B. K. 1974 Investigation of the aerodynamic noise generating region of a jet engine by means of the simple source fluid dilatation model. J. Acoust. Soc. Am. 56 (6), 1708–1721.CrossRefGoogle Scholar
Kiris, C., Barad, M., Housman, J., Sozer, E., Brehm, C. & Moini-Yekta, S.2014 The LAVA computational fluid dynamics solver. AIAA Paper 2014-0070.Google Scholar
Krothapalli, A., Rajkuperan, E., Alvi, F. & Lourenco, L. 1999 Flow field and noise characteristics of a supersonic impinging jet. J. Fluid Mech. 392, 155–181.Google Scholar
Lew, P., Uzun, A., Blaisdell, G. & Lyrintzis, A.2004 Effects of inflow forcing on jet noise using 3-D large eddy simulation. AIAA Paper 2004-516.Google Scholar
Liu, J., Corrigan, A., Kailasanath, K., Heeb, N., Munday, D. & Gutmark, E.2014 Numerical study of noise sources characteristics in an underexpanded jet flow. AIAA Paper 2014-2604.Google Scholar
Liu, J., Kailasanath, K., Boris, J. P., Heeb, N., Munday, D. & Gutmark, E.2012 Effect of nozzle-exit flow conditions on the flow and acoustic properties of imperfectly expanded supersonic jets. AIAA Paper 2012-2061.CrossRefGoogle Scholar
Lovely, D. & Haimes, R.1999 Shock detection from computational fluid dynamics results. AIAA Paper 1999-3285.Google Scholar
Lumley, J. 1967 The structure of inhomogeneous turbulent flows. In Atm. Turb. And Radio Wave Prop., Nauka, Moscow and Toulouse, France (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–178.Google Scholar
Lyrintzis, A. 2003 Surface integral methods in computational aeroacoustics from the (CFD) near-field to the (acoustic) far-field. Intl J. Aeroacoust. 2 (2), 95–128.Google Scholar
Meadows, K. R.1997 A study of fundamental shock noise mechanisms. NASA Tech. Paper 3605.Google Scholar
Michalke, A. 1977 On the effect of spatial source coherence on the radiation of jet noise. J. Sound Vib. 55 (3), 377–394.Google Scholar
Michalke, A. 1983 Some remarks on source coherence affecting jet noise. J. Sound Vib. 87 (1), 1–17.Google Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21 (3), 159–199.Google Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F. M., Vargas, A. & von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227 (10), 4825–4852.Google Scholar
Morris, P. & Tam, C. 1979 On the radiation of sound by the instability waves of a compressible axisymmetric jet. In Mechanics of Sound Generation in Flows, vol. 1, pp. 55–61.Google Scholar
Nagata, Y., Nonomura, T., Fujii, K. & Yamamoto, M. 2013 Analysis of acoustic-fields generated by a supersonic jet impinging on flat and curved inclined plates. Intl J. Aerosp. Lightweight Struct. 3 (3), 357–371.Google Scholar
Nakanishi, Y., Okamoto, K., Teramoto, S., Okunuki, T. & Tsutsumi, S. 2012 Acoustic characteristics of correctly-expanded supersonic hot impinging on an inclined flat plate. In Asian Joint Conferencee on Propulsion and Power, Xi’an, China, AJCPP Paper 2012-129.Google Scholar
Nakatogawa, T., Hirata, M. & Kukita, Y. 1971 Disintegration of a supersonic jet impinging normally on a flat plate. J. Spacecr. 8, 410–411.Google Scholar
Nonomura, T. & Fujii, K.2010 POD of aeroacoustic fields of a jet impinging on an inclined plate. AIAA Paper 2010-4019.Google Scholar
Nonomura, T. & Fujii, K.2011 Computational study of effects of near-wall turbulent structure on aeroacoustic waves from a supersonic jet impinging on an inclined plate. AIAA Paper 2011-2917.Google Scholar
Nonomura, T., Goto, Y. & Fujii, K. 2011 Aeroacoustic waves generated from a supersonic jet impinging on an inclined flat plate. Intl J. Aeroacoust. 10 (4), 401–426.CrossRefGoogle Scholar
Panda, J.2005 Identification of noise sources in high speed jets via correlation measurements – a review. AIAA Paper 2005-2844.Google Scholar
Panda, J. & Seasholtz, R. G. 2002 Experimental investigation of density fluctuations in high-speed jets and correlation with generated noise. J. Fluid Mech. 450, 97–130.Google Scholar
Panda, J., Seasholtz, R. G. & Elam, K. A. 2005 Investigation of noise sources in high-speed jets via correlation measurements. J. Fluid Mech. 537, 349–385.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pope, S. B. 2004 Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 6 (1), 35.Google Scholar
Powell, A. 1964 Theory of vortex sound. J. Acoust. Soc. Am. 36 (1), 177–195.Google Scholar
Powell, A. 1988 The sound-producing oscillations of round under-expanded jets impinging on normal plates. J. Acoust. Soc. Am. 83 (2), 515–533.Google Scholar
Proudman, I. 1952 The generation of noise by isotropic turbulence. Proc. R. Soc. Lond. A 214 (1116), 119–132.Google Scholar
Rackl, R.1973 Two causality correlation techniques. PhD thesis, University of British Columbia.Google Scholar
Rackl, R. & Siddon, T. E. 1979 Causality correlation analysis of flow noise with fluid dilatation as source fluctuation. J. Acoust. Soc. Am. 65 (5), 1147–1155.Google Scholar
Rienstra, S. W. & Hirschberg, A. 2004 An Introduction to Acoustics. Eindhoven University of Technology.Google Scholar
Rowley, C. W.2001 Modeling, simulation, and control of cavity flow oscillations. PhD thesis, California Institute of Technology.Google Scholar
Seiner, J. M.1974 The distribution of jet source strength intensity by means of a direct correlation technique. PhD thesis, Pennsylvania State University.Google Scholar
Shariff, K. & Manning, T. A. 2013 A ray tracing study of shock leakage in a model supersonic jet. Phys. Fluids 25, 076103.Google Scholar
Shur, M., Spalart, P. & Strelets, M. 2005a Noise prediction for increasingly complex jets. Part 2: applications. Intl J. Aeroacoust. 4 (4), 247–266.CrossRefGoogle Scholar
Shur, M., Spalart, P. & Strelets, M. 2005b Noise prediction for increasingly complex jets. Part I: methods and tests. Intl J. Aeroacoust. 4 (3), 213–246.CrossRefGoogle Scholar
Shur, M. L., Spalart, P. R., Strelets, M. Kh. & Travin, A. K. 2003 Towards the prediction of noise from jet engines. Intl J. Heat Fluid Flow 24 (4), 551–561; selected papers from the Fifth International Conference on Engineering Turbulence Modelling and Measurements.CrossRefGoogle Scholar
Siddon, T.1973 Noise source diagnostics using causality correlations. AGARD CP 132, pp. 7-1–7-13.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Q. Appl. Maths XLV(3), 561–590.Google Scholar
Suzuki, T., Bodony, D., Ryu, J. & Lele, S. K. 2007 Noise sources of high-Mach-number jets at low frequencies studied with a phased-array approach based on LES database. In Annual Research Briefs, Center for Turbulence Research, NASA Ames and Stanford University; http://ctr.stanford.edu/ResBriefs07/25_takao_pp287_302.pdf.Google Scholar
Tam, C. K. W. 1995 Supersonic jet noise. Annu. Rev. Fluid Mech. 27 (1), 17–43.Google Scholar
Tam, C. K. W. 1998 Influence of nozzle geometry on the noise of high-speed jets. AIAA J. 36 (8), 1396–1400.Google Scholar
Tam, C. K. W. & Burton, D. E. 1984 Sound generated by instability waves of supersonic flows. Part 2. Axisymmetric jets. J. Fluid Mech. 138, 273–295.Google Scholar
Tam, C. K. W. & Chen, P. 1994 Turbulent mixing noise from supersonic jets. AIAA J. 32 (9), 1774–1780.Google Scholar
Tam, C. K. W., Golebiowski, M. & Seiner, J. M.1996 On the two components of turbulent mixing noise from supersonic jets. AIAA Paper 1996–1716.Google Scholar
Tam, C. K. W., Viswanathan, K., Ahuja, K. K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–292.Google Scholar
Tsutsumi, S., Nonomura, T., Fujii, K., Nakanishi, Y., Teramoto, S. & Okamoto, K. 2012 Analysis of acoustic wave from supersonic jets impinging to an inclined plate. In ICCFD7-2012-3104, July 9–13, Big Island, Hawaii.Google Scholar
Tsutsumi, S., Takaki, R., Nakanishi, Y., Okamoto, K. & Teramoto, S.2014 Acoustic generation mechanism of a supersonic jet impinging on deflectors. AIAA Paper 2014-0882.Google Scholar
Varnier, J. 2001 Experimental study and simulation of rocket engine freejet noise. AIAA J. 39 (10), 1851–1859.Google Scholar
Viswanathan, K. 2002 Analysis of the two similarity components of turbulent mixing noise. AIAA J. 40 (9), 1735–1744.Google Scholar
Viswanathan, K. 2004 Aeroacoustics of hot jets. J. Fluid Mech. 516, 39–82.Google Scholar
Zaman, K. B. M. Q. 2012 Effect of initial boundary-layer state on subsonic jet noise. AIAA J. 50 (8), 1784–1795.Google Scholar