Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-08T04:23:37.804Z Has data issue: false hasContentIssue false
  • English
  • Français

New singularities for Stokes waves

Published online by Cambridge University Press:  31 May 2016

Samuel C. Crew  and
Philippe H. Trinh Open the ORCID record for Philippe H. Trinh [Opens in a new window]
Samuel C. Crew
Affiliation:
Lincoln College, University of Oxford, Oxford OX1 3DR, UK
Philippe H. Trinh*
Affiliation:
Lincoln College, University of Oxford, Oxford OX1 3DR, UK Oxford Centre for Industrial and Applied Mathematics, Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

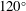In 1880, Stokes famously demonstrated that the singularity that occurs at the crest of the steepest possible water wave in infinite depth must correspond to a corner of $120^{\circ }$. Here, the complex velocity scales like 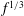$f^{1/3}$ where 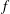$f$ is the complex potential. Later in 1973, Grant showed that for any wave away from the steepest configuration, the singularity 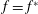$f=f^{\ast }$ moves into the complex plane, and is of order 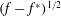$(f-f^{\ast })^{1/2}$ (Grant J. Fluid Mech., vol. 59, 1973, pp. 257–262). Grant conjectured that as the highest wave is approached, other singularities must coalesce at the crest so as to cancel the square-root behaviour. Despite recent advances, the complete singularity structure of the Stokes wave is still not well understood. In this work, we develop numerical methods for constructing the Riemann surface that represents the extension of the water wave into the complex plane. We show that a countably infinite number of distinct singularities exist on other branches of the solution, and that these singularities coalesce as Stokes’ highest wave is approached.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 256 - 283
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, G. A. & Graves-Morris, P. R. 1996 Padé Approximants. Cambridge University Press.CrossRefGoogle Scholar
Baker, G. R. & Xie, C. 2011 Singularities in the complex physical plane for deep water waves. J. Fluid Mech. 685, 83–116.CrossRefGoogle Scholar
Chapman, S. J., Trinh, P. H. & Witelski, T. P. 2013 Exponential asymptotics for thin film rupture. SIAM J. Appl. Maths 73 (1), 232–253.CrossRefGoogle Scholar
Chen, B. & Saffman, P. G. 1980 Numerical evidence for the existence of new types of gravity waves of permanent form on deep water. Stud. Appl. Maths 62, 1–21.CrossRefGoogle Scholar
Cokelet, E. D. 1977 Steep gravity waves in water of arbitrary uniform depth. Phil. Trans. R. Soc. Lond. A 286 (1335), 183–230.Google Scholar
Costin, O. & Costin, R. D. 2001 On the formation of singularities of solutions of nonlinear differential systems in antistokes directions. Invent. Math. 145 (3), 425–485.CrossRefGoogle Scholar
Dallaston, M. C. & McCue, S. W. 2010 Accurate series solutions for gravity-driven Stokes waves. Phys. Fluids 22 (8), 082104.CrossRefGoogle Scholar
Drennan, W. M.1988 Accurate calculations of Stokes water wave. PhD thesis, University of Waterloo.Google Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O. 2014 Complex singularity of a Stokes wave. J. Expl Theor. Phys. Lett. 98 (11), 675–679.CrossRefGoogle Scholar
Dyachenko, S. A., Lushnikov, P. M. & Korotkevich, A. O.2015 Branch cuts of Stokes wave on deep water. Part I: numerical solution and Padé approximation. Preprint, arXiv:1507.02784.Google Scholar
Grant, M. A. 1973 The singularity at the crest of a finite amplitude progressive Stokes wave. J. Fluid Mech. 59, 257–262.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1995 Parasitic capillary waves: a direct calculation. J. Fluid Mech. 301, 79–107.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1977 Theory of the almost-highest wave: the inner solution. J. Fluid Mech. 80, 721–741.CrossRefGoogle Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1978 Theory of the almost-highest wave. Part 2. Matching and analytic extension. J. Fluid Mech. 85, 769–786.CrossRefGoogle Scholar
Lushnikov, P. M.2015 Branch cuts of Stokes wave on deep water. Part II: structure and location of branch points in infinite set of sheets of Riemann surface. Preprint arXiv:1509.03393.Google Scholar
Lushnikov, P. M., Dyachenko, S. A. & Korotkevich, A. O. 2015 Branch cut singularity of Stokes wave on deep water. In The Ninth IMACS International Conference on Nonlinear Evolution Equations and Wave Phenomena. University of Georgia.Google Scholar
Olfe, D. B. & Rottman, J. W. 1980 Some new highest-wave solutions for deep-water waves of permanent form. J. Fluid Mech. 100 (4), 801–810.CrossRefGoogle Scholar
Schwartz, L. W.1972 Analytic continuation of Stokes’ expansion for gravity waves. PhD thesis, Stanford University.Google Scholar
Schwartz, L. W. 1974 Computer extension and analytic continuation of Stokes’ expansion for gravity waves. J. Fluid Mech. 62, 553–578.CrossRefGoogle Scholar
Schwartz, L. W. & Fenton, J. D. 1982 Strongly nonlinear waves. Annu. Rev. Fluid Mech. 14, 39–60.CrossRefGoogle Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Stokes, G. G. 1880a Appendices and supplement to a paper on the theory of oscillatory waves. In Mathematical and Physical Papers, vol. 1. Cambridge University Press.Google Scholar
Stokes, G. G. 1880b Appendix B. Considerations relative to the greatest height of oscillatory irrotational waves which can be propagated without change of form. In Mathematical and Physical Papers, vol. 1, pp. 225–228. Cambridge University Press.Google Scholar
Stokes, G. G. 1880c Letter from Stokes to Kelvin, 15 September 1880. In The Correspondence Between Sir George Gabriel Stokes and Sir William Thomson, Baron Kelvin of Largs (ed. Wilson, D. B.), vol. 2, pp. 498–501. Cambridge University Press.Google Scholar
Tanveer, S. 1991 Singularities in water waves and Rayleigh–Taylor instablity. Proc. R. Soc. Lond. A 435, 137–158.Google Scholar
Toland, J. F. 1978 On the existence of a wave of greatest height and Stokes’s conjecture. Proc. R. Soc. Lond. A 363 (1715), 469–485.Google Scholar
Toland, J. F. 1996 Stokes waves. Topol. Meth. Nonlinear Anal. 7, 1–48.CrossRefGoogle Scholar
Trinh, P. H. & Chapman, S. J. 2013a New gravity-capillary waves at low speeds. Part 1. Linear theory. J. Fluid Mech. 724, 367–391.CrossRefGoogle Scholar
Trinh, P. H. & Chapman, S. J. 2013b New gravity-capillary waves at low speeds. Part 2. Nonlinear theory. J. Fluid Mech. 724, 392–424.CrossRefGoogle Scholar
Trinh, P. H. & Chapman, S. J. 2015 Exponential asymptotics and problems with coalescing singularities. Nonlinearity 28 (5), 1229–1256.CrossRefGoogle Scholar
Trinh, P. H., Chapman, S. J. & Vanden-Broeck, J.-M. 2011 Do waveless ships exist? Results for single-cornered hulls. J. Fluid Mech. 685, 413–439.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1983 Some new gravity waves in water of finite depth. Phys. Fluids 26 (9), 2385–2387.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1986 Steep gravity waves: Havelock’s method revisited. Phys. Fluids 29 (9), 3084–3085.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar
Wehausen, J. V. & Laitone, E. V. 1960 Surface waves. In Handbuch der Physik (ed. Flugge, S. & Truesdell, C.), vol. IX, pp. 446–778. Springer.Google Scholar