Article contents
Naturally bounded plumes
Published online by Cambridge University Press: 01 February 2013
Abstract
This paper investigates theoretically the vertical evolution of a turbulent plume into a linearly stratified ambient fluid, by regarding it as composed of two distinct regions. In the first region, called the positive buoyant region, the plume buoyancy and the plume momentum act in the same upward direction, whereas in the second region, called the negative buoyant region, they act in opposite directions. In a first step, analytical expressions for the plume variables at the transition height (i.e. between the two regions) are obtained from one-dimensional conservation equations, using the plume entrainment model and under the Boussinesq approximation. In a second step, these variables are used in order to determine analytically the buoyancy and volume fluxes as well as the density deficit of the plume at its top. In this investigation, the transition height (denoted 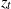 ${z}_{t} $) and the total plume height (denoted
${z}_{t} $) and the total plume height (denoted 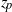 ${z}_{p} $) are obtained in the form of two integrals. These integrals are evaluated asymptotically in three different cases associated with particular flow regimes. Finally, the limit of the Boussinesq assumption for such flows is discussed.
${z}_{p} $) are obtained in the form of two integrals. These integrals are evaluated asymptotically in three different cases associated with particular flow regimes. Finally, the limit of the Boussinesq assumption for such flows is discussed.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 10
- Cited by


