Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T17:29:52.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-point Monin–Obukhov similarity in the convective atmospheric surface layer using matched asymptotic expansions

Published online by Cambridge University Press:  11 February 2019

Chenning Tong Open the ORCID record for Chenning Tong [Opens in a new window]  and
Mengjie Ding
Chenning Tong*
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
Mengjie Ding
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The multi-point Monin–Obukhov similarity (MMO) was recently proposed (Tong & Nguyen, J. Atmos. Sci., vol. 72, 2015, pp. 4337–4348) to address the issue of incomplete similarity in the framework of the original Monin–Obukhov similarity theory (MOST). MMO hypothesizes the following: (1) The surface-layer turbulence, defined to consist of eddies that are entirely inside the surface layer, has complete similarity, which however can only be represented by multi-point statistics, requiring a horizontal characteristic length scale (absent in MOST). (2) The Obukhov length 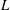$L$ is also the characteristic horizontal length scale; therefore, all surface-layer multi-point statistics, non-dimensionalized using the surface-layer parameters, depend only on the height and separations between the points, non-dimensionalized using 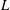$L$. However, similar to MOST, MMO was also proposed as a hypothesis based on phenomenology. In this work we derive MMO analytically for the case of the horizontal Fourier transforms of the velocity and potential temperature fluctuations, which are equivalent to the two-point horizontal differences of these variables, using the spectral forms of the Navier–Stokes and the potential temperature equations. We show that, for the large-scale motions (wavenumber 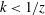$k<1/z$) in a convective surface layer, the solution is uniformly valid with respect to $z$ (i.e. 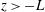as $z$ decreases from $z>-L$ to 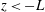$z<-L$), where $z$ is the height from the surface. However, for 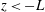$z<-L$ the solution is not uniformly valid with respective to 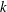$k$ as it increases from 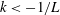$k<-1/L$ to 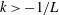$k>-1/L$, resulting in a singular perturbation problem, which we analyse using the method of matched asymptotic expansions. We show that (1) 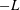$-L$ is the characteristic horizontal length scale, and (2) the Fourier transforms satisfy MMO with the non-dimensional wavenumber 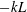$-kL$ as the independent similarity variable. Two scaling ranges, the convective range and the dynamic range, discovered for 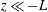$z\ll -L$ in Tong & Nguyen (2015) are obtained. We derive the leading-order spectral scaling exponents for the two scaling ranges and the corrections to the scaling ranges for finite ratios of the length scales. The analysis also reveals the dominant dynamics in each scaling range. The analytical derivations of the characteristic horizontal length scale (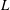$L$) and the validity of MMO for the case of two-point horizontal separations provide strong support to MMO for general multi-point velocity and temperature differences.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 640 - 669
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Betchov, R. & Yaglom, A. M. 1971 Comments on the theory of similarity as applied to turbulence in an unstable stratified fluid. Izv. Akad. Nauk. Ser. Fiz. Atmos. Okeana 7, 829–832; English translation.Google Scholar
Businger, J. A. 1973 A note on free convection. Boundary-Layer Meteorol. 4, 323–326.Google Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28, 181–189.Google Scholar
Caughey, S. J. & Palmer, S. G. 1979 Some aspects of turbulence structure through the depth of the convective boundary layer. Q. J. R. Meteorol. Soc. 105, 811–827.Google Scholar
Cousteix, J. & Mauss, J. 2007 Asymptotic Analysis and Boundary Layers. Springer.Google Scholar
Ding, M., Nguyen, K. X., Liu, S., Otte, M. J. & Tong, C. 2018 Investigation of the pressure–strain-rate correlation and pressure fluctuations in convective and near neutral atmospheric surface layers. J. Fluid Mech. 854, 88–120.Google Scholar
Grachev, A. A. W., Fairall, C. & Zilitinkevich, S. S. 1997 Surface-layer scaling for the convection induced stress regime. Boundary-Layer Meteorol. 83, 423–439.Google Scholar
Kader, B. A. 1988 Three-layer structure of an unstably stratified atmospheric surface layer. Izv. Akad. Nauk. Ser. Fiz. Atmos. Okeana 24, 907–918; English translation.Google Scholar
Kaimal, J. C. 1978 Horizontal velocity spectra in an unstable surface layer. J. Atmos. Sci. 35, 18–24.Google Scholar
Kaimal, J. C., Wyngaard, J. C., Izumi, Y. & Coté, O. R. 1972 Spectral characteristic of surface-layer turbulence. Q. J. R. Meteorol. Soc. 98, 563–589.Google Scholar
Kosović, B. 1997 Subgrid-scale modelling for the large-eddy simulation of high-Reynolds-number boundary layer.. J. Fluid Mech. 336, 151–182.Google Scholar
Lumley, J. L. & Panofsky, H. A. 1964 The Structure of Atmospheric Turbulence, Interscience Monographs and Texts in Physics and Astronomy, vol. 12. Interscience.Google Scholar
Lundgren, T. S. 2003 Kolmogorov turbulence by matched asymptotic expansions. Phys. Fluids 15, 1074–1081.Google Scholar
Moeng, C.-H. 1984 A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.Google Scholar
Moeng, C. H. & Wyngaard, J. C. 1988 Spectral analysis of large-eddy simulations of the convective boundary layer. J. Atmos. Sci. 45, 3573–3587.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the ground layer of the atmosphere. Trans. Inst. Teoret. Geofiz. Akad. Nauk SSSR 151, 163–187.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. MIT Press.Google Scholar
Nguyen, K. X., Horst, T. W., Oncley, S. P. & Tong, C. 2013 Measurements of the budgets of the subgrid-scale stress and temperature flux in a convective atmospheric surface layer. J. Fluid Mech. 729, 388–422.Google Scholar
Nguyen, K. X. & Tong, C. 2015 Investigation of subgrid-scale physics in the convective atmospheric surface layer using the budgets of the conditional mean subgrid-scale stress and temperature flux. J. Fluid Mech. 772, 295–329.Google Scholar
Obukhov, A. M. 1946 Turbulence in the atmosphere with inhomogeneous temperature. Trans. Inst. Teoret. Geofiz. Akad. Nauk SSSR 1, 95–115.Google Scholar
Otte, M. J. & Wyngaard, J. C. 2001 Stably stratified interfacial-layer turbulence from large-eddy simulation. J. Atmos. Sci. 58, 3424–3442.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C.-H. 1994 A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 71, 247–276.Google Scholar
Sullivan, P. P., Mcwilliams, J. C. & Moeng, C.-H. 1996 A grid nesting method for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 80, 167–202.Google Scholar
Sykes, R. I., Henn, D. S. & Lewellen, W. S. 1993 Surface-layer description under free-convection conditions. Q. J. R. Meteorol. Soc. 119, 409–421.Google Scholar
Tong, C. & Ding, M. 2018 Monin-Obukhov similarity and local-free-convection scaling in the atmospheric boundary layer using matched asymptotic expansions. J. Atmos. Sci. 75, 3691–3701.Google Scholar
Tong, C. & Nguyen, K. X. 2015 Multipoint Monin–Obukhov similarity and its application to turbulence spectra in the convective atmospheric surface layer. J. Atmos. Sci. 72, 4337–4348.Google Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. The Parabolic Press.Google Scholar
Wyngaard, J. C. & Coté, O. R. 1971 The budgets of turbulent kinetic energy and temperature variance in the atmospheric surface layer. J. Atmos. Sci. 28, 190–201.Google Scholar
Wyngaard, J. C., Coté, O. R. & Izumi, Y. 1971 Local free convection, similarity, and the budgets of shear stress and heat flux. J. Atmos. Sci. 28, 1171–1182.Google Scholar
Yaglom, A. M. 1994 Fluctuation spectra and variances in convective turbulent boundary layers: a reevaluation of old models. Phys. Fluids 6, 962–972.Google Scholar
Zilitinkevich, S. S. 1971 On the turbulence and diffusion under free convection conditions. Izv. Akad. Nauk. Ser. Fiz. Atmos. Okeana 7, 1263–1269.Google Scholar
Zilitinkevich, S. S., Hunt, J. C. R., Esau, I. N., Grachev, A. A., Lalas, D. P., Akylas, E., Tombrou, M., Fairall, C. W., Fernando, H. J. S., Baklanov, A. A. & Joffre, S. M. 2006 The influence of large convective eddies on the surface-layer turbulence. Q. J. R. Meteorol. Soc. 132, 1423–1456.Google Scholar