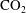Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T13:33:51.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple steady states in exchange flows across faults and the dissolution of $\text{CO}_{2}$

Published online by Cambridge University Press:  16 March 2015

Andrew W. Woods ,
Marc Hesse ,
Rachel Berkowitz  and
Kyung Won Chang
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Marc Hesse
Affiliation:
Department of Geological Sciences, University of Texas, Austin, TX 78712, USA
Rachel Berkowitz
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Kyung Won Chang
Affiliation:
Department of Geological Sciences, University of Texas, Austin, TX 78712, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a model of the steady exchange flows which may develop between two aquifers at different levels in the geological strata and across which there is an unstable density stratification, as a result of their connection through a series of fractures. We show that in general there are multiple steady exchange flows which can develop, depending on the initial conditions, and which may involve a net upwards or downwards volume flux. We also show that there is a family of equilibrium exchange flows with zero net volume flux, each characterised by a different interlayer flux of buoyancy. We present experiments which confirm our simplified model of the exchange flow. Such exchange flows may supply unsaturated water from a deep aquifer to drive dissolution of a structurally trapped pool of geologically stored 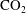$\text{CO}_{2}$, once the water in the aquifer containing the trapped pool of 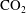$\text{CO}_{2}$ has become saturated in 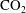$\text{CO}_{2}$, and hence relatively dense. Such exchange flows may also lead to cross-contamination of aquifer fluids, which may be of relevance in assessing risks of geological storage systems.

JFM classification

Convection: Convection Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 229 - 241
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bear, J. 1981 Introduction to Flow in Porous Media. Wiley.Google Scholar
Bennion, B. & Bachu, S. 2008 Drainage and imbibition relative permeability relationships for supercritical $\text{CO}_{2}$ /Brine and $\text{H}_{2}\text{S}$ /Brine systems in intergranular sandstone, carbonate, shale and anhydrite rocks. SPE Reservoir Eval. Engng 11 (3), 487–496.Google Scholar
Chen, C. & Zhang, D. 2010 Pore-scale simulation of density-driven convection in fractured porous media during geological $\text{CO}_{2}$ sequestration. Water Resour. Res. 46, W11527.Google Scholar
Croucher, A. E. & O’Sullivan, M. J. 1995 The Henry problem of salt–water intrusion. Water Resour. Res. 31, 1809–1814.CrossRefGoogle Scholar
Diersch, H.-J. & Kolditz, O. 2002 Variable-density flow and transport in porous media: approaches and challenges. Adv. Water Resour. 25, 899–944.CrossRefGoogle Scholar
Ennis-King, J. & Paterson, L. 2007 Coupling of geochemical reactions and convective mixing in the long-term geological storage of carbon dioxide. Intl J. Greenh. Gas Control 1, 86–93.Google Scholar
Farcas, A. & Woods, A. W. 2009 The effect of drainage on the capillary retention of $\text{CO}_{2}$ in a layered permeable rock. J. Fluid Mech. 618, 349–359.Google Scholar
Flowers, T. & Hunt, J. 2007 Viscous and gravitational contributions to mixing during vertical brine transport in water-saturated porous media. Water Resour. Res. 43, WR004773.Google Scholar
Fried, J. J. & Combarnous, M. A. 1971 Dispersion in porous media. Adv. Hydrosci. 7, 169–282.Google Scholar
Green, C. P. & Ennis-King, K. 2010 Effect of vertical heterogeneity on long-term migration of $\text{CO}_{2}$ in saline formations. Transp. Porous Med. 82, 31–47.CrossRefGoogle Scholar
Hesse, M., Tchelpi, M. & Orr, L. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.CrossRefGoogle Scholar
Hewitt, D., Neufeld, J. & Lister, J. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.CrossRefGoogle Scholar
Intergovernmental Panel on Climate Change 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge University Press.Google Scholar
Kuznetsov, A. V. & Nield, D. A. 2011 The effects of combined horizontal and vertical heterogeneity on the onset of convection in a porous medium with vertical throughflow. Transp. Porous Med. 90, 465–478.Google Scholar
Kuznetsov, A. & Nield, D. A. 2012 The effect of strong heterogeneity and strong throughflow on the onset of convection in a porous medium: periodic and localized variation. Transp. Porous Med. 92, 289–298.Google Scholar
Levy, M. & Berkowitz, B. 2003 Measurement and analysis of non-Fickian dispersion in heterogeneous porous media. J. Contam. Hydrol. 64 (3–4), 203–226.Google Scholar
Lindeberg, E. & Wessel-Berg, D. 1997 Vertical convection in an aquifer column under a gas cap of $\text{CO}_{2}$ . Energy Convers. Manage. 38, S229–S234.CrossRefGoogle Scholar
Menand, T., Raw, A. & Woods, A. W. 2003 Thermal inertia and reversing buoyancy in flow in porous media. Geophys. Res. Lett. 30 (6), 1241–1245.CrossRefGoogle Scholar
Oldenburg, C. M. & Rinaldi, A. P. 2011 Buoyancy effects on upward brine displacement caused by $\text{CO}_{2}$ injection. Transp. Porous Med. 87 (2), 525–540.Google Scholar
Pau, G., Bell, J. B., Pruess, K., Almgren, A. & Lijenski, M. 2009 High resolution simulation and characterisation of density driven flow in $\text{CO}_{2}$ storage in saline aquifers. Adv. Water Resour. 33, 443–455.Google Scholar
Phillips, O. M. 1991 Flow and Reaction in Permeable Rocks. Cambridge University Press.Google Scholar
Pruess, K., Xu, T., Apps, J. & García, J. 2003 Numerical modeling of aquifer disposal of $\text{CO}_{2}$ . SPE J. 8, 49–60.CrossRefGoogle Scholar
Ranganathan, P., Farajzadeh, R., Bruining, H. & Zitha, P. 2012 Numerical simulation of natural convection in heterogeneous porous media for $\text{CO}_{2}$ geological storage. Trans. Porous Med. 95, 25–54.CrossRefGoogle Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. Jr 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Scheidegger, A. E. 1961 General theory of dispersion in porous media. J. Geophys. Res. 66, 3273–3274.Google Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2014 Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315.Google Scholar
Tartakovsky, A. & Meakin, P. 2005 A smoothed particle hydrodynamics model for miscible flow in three-dimensional fractures and the two-dimensional Rayleigh–Taylor instability. J. Comput. Phys. 207, 610–624.Google Scholar
Woods, A. W. 2015 Flow in Porous Rocks. pp. 1–289. Cambridge University Press.Google Scholar
Woods, A. W. & Espie, A. 2012 Controls on the dissolution of $\text{CO}_{2}$ plumes in structural traps in deep saline aquifers. Geophys. Res. Lett. 39, L08401.CrossRefGoogle Scholar