Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T14:30:26.123Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiphase plumes in a stratified ambient

Published online by Cambridge University Press:  23 April 2019

Nicola Mingotti Open the ORCID record for Nicola Mingotti [Opens in a new window]  and
Andrew W. Woods Open the ORCID record for Andrew W. Woods [Opens in a new window]
Nicola Mingotti
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report on experiments of turbulent particle-laden plumes descending through a stratified environment. We show that provided the characteristic plume speed 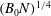$(B_{0}N)^{1/4}$ exceeds the particle fall speed, where the plume buoyancy flux is 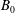$B_{0}$ and the Brunt–Väisälä frequency is 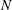$N$, then the plume is arrested by the stratification and initially intrudes at the neutral height associated with a single-phase plume of the same buoyancy flux. If the original fluid phase in the plume has density equal to that of the ambient fluid at the source, then as the particles sediment from the intruding fluid, the fluid finds itself buoyant and rises, ultimately intruding at a height of about $0.58\pm 0.03$ of the original plume height, consistent with new predictions we present based on classical plume theory. We generalise this result, and show that if the buoyancy flux at the source is composed of a fraction 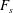$F_{s}$ associated with the buoyancy of the source fluid, and a fraction 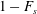$1-F_{s}$ from the particles, then following the sedimentation of the particles, the plume fluid intrudes at a height 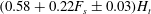$(0.58+0.22F_{s}\pm 0.03)H_{t}$, where 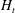$H_{t}$ is the maximum plume height. This is key for predictions of the environmental impact of any material dissolved in the plume water which may originate from the particle load. We also show that the particles sediment at their fall speed through the fluid below the maximum depth of the plume as a cylindrical column whose area scales as the ratio of the particle flux at the source to the fall speed and concentration of particles in the plume at the maximum depth of the plume before it is arrested by the stratification. We demonstrate that there is negligible vertical transport of fluid in this cylindrical column, but a series of layers of high and low particle concentration develop in the column with a vertical spacing which is given by the ratio of the buoyancy of the particle load and the background buoyancy gradient. Small fluid intrusions develop at the side of the column associated with these layers, as dense parcels of particle-laden fluid convect downwards and then outward once the particles have sedimented from the fluid, with a lateral return flow drawing in ambient fluid. As a result, the pattern of particle-rich and particle-poor layers in the column gradually migrates upwards owing to the convective transport of particles between the particle-rich layers superposed on the background sedimentation. We consider the implications of the results for mixing by bubble plumes, for submarine blowouts of oil and gas and for the fate of plumes of waste particles discharged at the ocean surface during deep-sea mining.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 292 - 312
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asaeda, T. & Imberger, J. 1993 Structure of bubble plumes in linearly stratified environments. J. Fluid Mech. 249, 35–57.Google Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Bush, J. W. M., Thurber, B. A. & Blanchette, F. 2003 Particle clouds in homogeneous and stratified environments. J. Fluid Mech. 489, 29–54.Google Scholar
Chan, G. K. Y., Chow, A. C. & Adams, E. E. 2015 Effects of droplet size on intrusions of sub-surface oil spills. Environ. Fluid Mech. 15 (5), 959–973.Google Scholar
Coulin, J., Haley, P. J., Jana, S., Kulkarni, C. S., Lermusiaux, P. F. & Peacock, T. 2017 Environmental ocean and plume modeling for deep sea mining in the Bismarck Sea. OCEANS 2017 – Anchorage. IEEE.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Johansen, O., Rye, H. & Cooper, C. 2003 Deepspill field study of a simulated oil and gas blowout in deep water. Spill Sci. Technol. Bull. 8, 433–443.Google Scholar
Lemckert, C. J. & Imberger, J. 1993 Energetic bubble plumes in arbitrary stratification. J. Hydraul. Engng ASCE 119, 680–703.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
Lippert, M. C. & Woods, A. W. 2018 Particle fountains in a confined environment. J. Fluid Mech. 855, 28–42.Google Scholar
McDougall, T. J. 1978 Bubble plumes in stratified environments. J. Fluid Mech. 85, 655–672.Google Scholar
Milgram, J. H. 1983 Mean flow in round bubble plumes. J. Fluid Mech. 133, 345–376.Google Scholar
Mingotti, N. & Woods, A. W. 2015 On the transport of heavy particles through an upward displacement-ventilated space. J. Fluid Mech. 772, 478–507.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 19560011.Google Scholar
Neto, I. E. L., Cardoso, S. S. S. & Woods, A. W. 2016 On mixing a density interface by a bubble plume. J. Fluid Mech. 802, R3.Google Scholar
Oster, G. & Yamamoto, M. 1963 Density gradient techniques. Chem. Rev. 63 (3), 257–268.Google Scholar
Peacock, T., Blanchette, F. & Bush, J. W. M. 2005 The stratified Boycott effect. J. Fluid Mech. 529, 33–49.Google Scholar
Seol, D., Bryant, D. B. & Socolofsky, S. A. 2009 Measurement of behavioral properties of entrained ambient water in a stratified bubble plume. J. Hydraul. Engng ASCE 135, 983–988.Google Scholar
Socolofsky, S. A. & Adams, E. E. 2005 Role of slip velocity in the behavior of stratified multiphase plumes. J. Hydraul. Engng ASCE 131, 273–282.Google Scholar
Socolofsky, S. A., Adams, E. E. & Sherwood, C. R. 2011 Formation dynamics of subsurface hydrocarbon intrusions following the Deepwater Horizon blowout. Geophys. Res. Lett. 38, L09602.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar