Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-02T20:37:27.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Moffatt eddies in electrohydrodynamics flows: numerical simulations and analyses

Published online by Cambridge University Press:  06 December 2022

Xuerao He Open the ORCID record for Xuerao He [Opens in a new window] ,
Zhihao Sun  and
Mengqi Zhang Open the ORCID record for Mengqi Zhang [Opens in a new window]
Xuerao He
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, 117575 Singapore
Zhihao Sun
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, 117575 Singapore School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, PR China
Mengqi Zhang*
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, 117575 Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

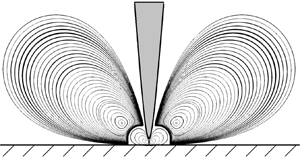
We study numerically a sequence of eddies in two-dimensional electrohydrodynamics (EHD) flows of a dielectric liquid, driven by an electric potential difference between a hyperbolic blade electrode and a flat plate electrode (or the blade–plate configuration). The electrically driven flow impinges on the plate to generate vortices, which resemble Moffatt eddies (Moffatt, J. Fluid Mech., vol. 18, 1964, pp. 1–18). Such a phenomenon in EHD was first reported in the experimental work of Perri et al. (J. Fluid Mech., vol. 900, 2020, A12). We conduct direct numerical simulations of the EHD flow with three Moffatt-type eddies in a large computational domain at moderate electric Rayleigh numbers ($T$, quantifying the strength of the electric field). The ratios of size and intensity of the adjacent eddies are examined, and they can be compared favourably to the theoretical prediction of Moffatt; interestingly, the quantitative comparison is remarkably accurate for the two eddies in the far field. Our investigation also shows that a larger $T$ strengthens the vortex intensity, and a stronger charge diffusion effect enlarges the vortex size. A sufficiently large $T$ can further result in an oscillating flow, consistent with the experimental observation. In addition, a global stability analysis of the steady blade–plate EHD flow is conducted. The global mode is characterised in detail at different values of $T$. When $T$ is large, the confinement effect of the geometry in the centre region may lead to an increased oscillation frequency. This work contributes to the quantitative characterisation of the Moffatt-type eddies in EHD flows.

JFM classification

Vortex Flows: Vortex dynamics Complex Fluids: Dielectrics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A14
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akervik, E., Brandt, L., Henningson, D.S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.CrossRefGoogle Scholar
Alleborn, N., Nandakumar, K., Raszillier, H. & Durst, F. 1997 Further contributions on the two-dimensional flow in a sudden expansion. J. Fluid Mech. 330, 169–188.Google Scholar
Anderson, E., et al. 1999 LAPACK Users’ Guide. SIAM.CrossRefGoogle Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. & Lingwood, R. 2015 Global linear instability of the rotating-disk flow investigated through simulations. J. Fluid Mech. 765, 612–631.CrossRefGoogle Scholar
Atten, P. 1996 Electrohydrodynamic instability and motion induced by injected space charge in insulating liquids. IEEE Trans. Dielec. Elec. Insul. 3 (1), 1–17.CrossRefGoogle Scholar
Atten, P. & Lacroix, J. 1979 Non-linear hydrodynamic stability of liquids subjected to unipolar injection. J. Méc. 18 (3), 469–510.Google Scholar
Atten, P., Malraison, B. & Zahn, M. 1997 Electrohydrodynamic plumes in point-plane geometry. IEEE Trans. Dielec. Elec. Insul. 4 (6), 710–718.Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Biswas, G., Breuer, M. & Durst, F. 2004 Backward-facing step flows for various expansion ratios at low and moderate Reynolds numbers. J. Fluids Engng 126 (3), 362–374.CrossRefGoogle Scholar
Biswas, S. & Kalita, J.C. 2016 Moffatt vortices in the lid-driven cavity flow. J. Phys.: Conf. Ser. 759, 012081.Google Scholar
Biswas, S. & Kalita, J.C. 2018 Moffatt eddies in the driven cavity: a quantification study by an HOC approach. Comput. Maths Applics. 76 (3), 471–487.CrossRefGoogle Scholar
Burggraf, O.R. 1966 Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 24 (1), 113–151.CrossRefGoogle Scholar
Castellanos, A. 1991 Coulomb-driven convection in electrohydrodynamics. IEEE Trans. Dielec. Elec. Insul. 26 (6), 1201–1215.CrossRefGoogle Scholar
Castellanos, A. 1998 Electrohydrodynamics. Springer.Google Scholar
Chevalier, M., Lundbladh, A. & Henningson, D.S. 2007 Simson – a pseudo-spectral solver for incompressible boundary layer flow. Tech. Rep. TRITA-MEK 2007:07 KTH Mechanics.Google Scholar
Chicón, R., Castellanos, A. & Martin, E. 1997 Numerical modelling of Coulomb-driven convection in insulating liquids. J. Fluid Mech. 344, 43–66.CrossRefGoogle Scholar
Daaboul, M., Traoré, P., Vázquez, P. & Louste, C. 2017 Study of the transition from conduction to injection in an electrohydrodynamic flow in blade-plane geometry. J. Electrostat. 88, 71–75.Google Scholar
Davis, A. 1989 Thermocapillary convection in liquid bridges: solution structure and eddy motions. Phys. Fluids 1 (3), 475–479.CrossRefGoogle Scholar
Davis, A. & O'Neill, M. 1977 Separation in a slow linear shear flow past a cylinder and a plane. J. Fluid Mech. 81 (3), 551–564.CrossRefGoogle Scholar
Davis, A., O'Neill, M., Dorrepaal, J. & Ranger, K. 1976 Separation from the surface of two equal spheres in Stokes flow. J. Fluid Mech. 77 (4), 625–644.CrossRefGoogle Scholar
Feng, Z., Zhang, M., Vázquez, P.A. & Shu, C. 2021 Deterministic and stochastic bifurcations in two-dimensional electroconvective flows. J. Fluid Mech. 922, A20.CrossRefGoogle Scholar
Fenn, J.B., Mann, M., Meng, C.K., Wong, S.F. & Whitehouse, C.M. 1989 Electrospray ionization for mass spectrometry of large biomolecules. Science 246 (4926), 64–71.CrossRefGoogle ScholarPubMed
Fischer, P.F., Lottes, J.W. & Kerkemeier, S.G. 2008 Nek5000 web page. Available at: http://nek5000.mcs.anl.gov.Google Scholar
Grassi, W. & Testi, D. 2006 Heat transfer enhancement by electric fields in several heat exchange regimes. Ann. N.Y. Acad. Sci. 1077 (1), 527–569.CrossRefGoogle ScholarPubMed
Haidara, M. & Atten, P. 1985 Role of EHD motion in the electrical conduction of liquids in a blade-plane geometry. IEEE Trans. Ind. Applics. IA-21 (3), 709–714.Google Scholar
Kirkinis, E. & Davis, S. 2014 Moffatt vortices induced by the motion of a contact line. J. Fluid Mech. 746, R3.Google Scholar
Kuhlmann, H.C., Nienhüser, C. & Rath, H.J. 1999 The local flow in a wedge between a rigid wall and a surface of constant shear stress. J. Engng Maths 36 (3), 207–218.CrossRefGoogle Scholar
Lacroix, J., Atten, P. & Hopfinger, E. 1975 Electro-convection in a dielectric liquid layer subjected to unipolar injection. J. Fluid Mech. 69 (3), 539–563.CrossRefGoogle Scholar
Lehoucq, R.B. & Sorensen, D.C. 1996 Deflation techniques for an implicitly restarted Arnoldi iteration. SIAM J. Matrix Anal. Applics. 17 (4), 789–821.CrossRefGoogle Scholar
Lesshafft, L. 2015 Linear global stability of a confined plume. Theor. Appl. Mech. Lett. 5 (3), 126–128.CrossRefGoogle Scholar
Magalhães, J.P., Albuquerque, D.M., Pereira, J.M. & Pereira, J.C. 2013 Adaptive mesh finite-volume calculation of 2D lid-cavity corner vortices. J. Comput. Phys. 243, 365–381.CrossRefGoogle Scholar
Malhotra, C.P., Weidman, P.D. & Davis, A.M. 2005 Nested toroidal vortices between concentric cones. J. Fluid Mech. 522, 117–139.CrossRefGoogle Scholar
Malraison, B. & Atten, P. 1982 Chaotic behavior of instability due to unipolar ion injection in a dielectric liquid. Phys. Rev. Lett. 49, 723–726.CrossRefGoogle Scholar
Malyuga, V. 2005 Viscous eddies in a circular cone. J. Fluid Mech. 522, 101–116.CrossRefGoogle Scholar
McCluskey, F. & Atten, P. 1988 Modifications to the wake of a wire across Poiseuille flow due to a unipolar space charge. J. Fluid Mech. 197, 81–104.CrossRefGoogle Scholar
Meliga, P. & Chomaz, J.-M. 2011 Global modes in a confined impinging jet: application to heat transfer and control. Theor. Comput. Fluid Dyn. 25 (1), 179–193.CrossRefGoogle Scholar
Moffatt, H. 2019 Singularities in fluid mechanics. Phys. Rev. Fluids 4 (11), 110502.CrossRefGoogle Scholar
Moffatt, H. & Duffy, B. 1980 Local similarity solutions and their limitations. J. Fluid Mech. 96 (2), 299–313.CrossRefGoogle Scholar
Moffatt, H. & Mak, V. 1999 Corner singularities in three-dimensional Stokes flow. In IUTAM Symposium on Non-linear Singularities in Deformation and Flow (ed. D. Durban & J.R.A. Pearson), pp. 21–26. Springer.Google Scholar
Moffatt, H.K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.Google Scholar
Pan, M., He, D. & Pan, K. 2021 Energy stable finite element method for an electrohydrodynamic model with variable density. J. Comput. Phys. 424, 109870.CrossRefGoogle Scholar
Park, J.H., Suh, Y.K., Jeon, E.C. & Kim, J.W. 2004 A numerical study on the oscillatory impinging jet. SAE Tech. Paper 2004-01-1736.Google Scholar
Patera, A.T. 1984 A spectral element method for fluid dynamics: laminar flow in a channel expansion. J. Comput. Phys. 54 (3), 468–488.CrossRefGoogle Scholar
Pérez, A. & Castellanos, A. 1989 Role of charge diffusion in finite-amplitude electroconvection. Phys. Rev. A 40 (10), 5844.CrossRefGoogle ScholarPubMed
Pérez, A., Traore, P., Koulova-Nenova, D. & Romat, H. 2009 Numerical study of an electrohydrodynamic plume between a blade injector and a flat plate. IEEE Trans. Dielec. Elec. Insul. 16 (2), 448–455.CrossRefGoogle Scholar
Pérez, A.T., Vázquez, P.A. & Castellanos, A. 1995 Dynamics and linear stability of charged jets in dielectric liquids. IEEE Trans. Ind. Applics. 31 (4), 761–767.CrossRefGoogle Scholar
Perri, A.E., Sankaran, A., Kashir, B., Staszel, C., Schick, R.J., Mashayek, F. & Yarin, A.L. 2020 Electrically driven toroidal Moffatt vortices: experimental observations. J. Fluid Mech. 900, A12.CrossRefGoogle Scholar
Perri, A.E., Sankaran, A., Staszel, C., Schick, R.J., Mashayek, F. & Yarin, A.L. 2021 The particle image velocimetry of vortical electrohydrodynamic flows of oil near a high-voltage electrode tip. Exp. Fluids 62 (2), 27.CrossRefGoogle Scholar
Sankaran, A., Staszel, C., Mashayek, F. & Yarin, A.L. 2018 Faradaic reactions mechanisms and parameters in charging of oils. Electrochim. Acta 268, 173–186.CrossRefGoogle Scholar
Scott, J.F. 2013 Moffatt-type flows in a trihedral cone. J. Fluid Mech. 725, 446–461.CrossRefGoogle Scholar
Shankar, P. 1997 Three-dimensional eddy structure in a cylindrical container. J. Fluid Mech. 342, 97–118.CrossRefGoogle Scholar
Shankar, P. 1998 Three-dimensional Stokes flow in a cylindrical container. Phys. Fluids 10 (3), 540–549.CrossRefGoogle Scholar
Shankar, P. 2000 On Stokes flow in a semi-infinite wedge. J. Fluid Mech. 422, 69–90.CrossRefGoogle Scholar
Shankar, P. 2005 Moffatt eddies in the cone. J. Fluid Mech. 539, 113–135.CrossRefGoogle Scholar
Suh, Y.K. 2012 Modeling and simulation of ion transport in dielectric liquids – fundamentals and review. IEEE Trans. Dielec. Elec. Insul. 19 (3), 831–848.Google Scholar
Sun, Z., Sun, D., Hu, J., Traoré, P., Yi, H.-L. & Wu, J. 2020 Experimental study on electrohydrodynamic flows of a dielectric liquid in a needle–plate configuration under direct/alternating current electric field. J. Electrostat. 106, 103454.CrossRefGoogle Scholar
Taneda, S. 1979 Visualization of separating Stokes flows. J. Phys. Soc. Japan 46 (6), 1935–1942.CrossRefGoogle Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39 (4), 249–315.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43 (1), 319–352.CrossRefGoogle Scholar
Tobazeon, R., Haidara, M. & Atten, P. 1984 Ion injection and Kerr plots in liquids with blade-plane electrodes. J. Phys. D 17 (6), 1293–1301.CrossRefGoogle Scholar
Traore, P., Wu, J., Louste, C., Pelletier, Q. & Dascalescu, L. 2014 Electrohydrodynamic plumes due to autonomous and nonautonomous charge injection by a sharp blade electrode in a dielectric liquid. IEEE Trans. Ind. Applics. 51 (3), 2504–2512.CrossRefGoogle Scholar
Vázquez, P., Pérez, A. & Castellanos, A. 1996 Thermal and electrohydrodynamic plumes: a comparative study. Phys. Fluids 8 (8), 2091–2096.CrossRefGoogle Scholar
Wakiya, S. 1976 Axisymmetric flow of a viscous fluid near the vertex of a body. J. Fluid Mech. 78 (4), 737–747.CrossRefGoogle Scholar
Weidman, P.D. & Calmidi, V. 1999 Instantaneous Stokes flow in a conical apex aligned with gravity and bounded by a stress-free surface. SIAM J. Appl. Maths 59 (4), 1520–1531.Google Scholar
Wu, J., Traore, P., Louste, C., Koulova, D. & Romat, H. 2013 Direct numerical simulation of electrohydrodynamic plumes generated by a hyperbolic blade electrode. J. Electrostat. 71 (3), 326–331.CrossRefGoogle Scholar
Yan, Z., Louste, C., Traoré, P. & Romat, H. 2013 Velocity and turbulence intensity of an EHD impinging dielectric liquid jet in blade–plane geometry. IEEE Trans. Ind. Applics. 49 (5), 2314–2322.CrossRefGoogle Scholar
Zhang, M. 2016 Weakly nonlinear stability analysis of subcritical electrohydrodynamic flow subject to strong unipolar injection. J. Fluid Mech. 792, 328–363.CrossRefGoogle Scholar
Zhang, M., Martinelli, F., Wu, J., Schmid, P.J. & Quadrio, M. 2015 Modal and non-modal stability analysis of electrohydrodynamic flow with and without cross-flow. J. Fluid Mech. 770, 319–349.CrossRefGoogle Scholar

He et al. supplementary movie 1

Time-periodic oscillation of charge density at the electric Taylor number T=30,000. The other parameters are C=5, M=50, Fe=5,000, R=0.05.

Download He et al. supplementary movie 1(Video)
Video 5 MB

He et al. supplementary movie 2

Time-periodic oscillation of charge density at the electric Taylor number T=40,000. The other parameters are C=5, M=50, Fe=5,000, R=0.05.

Download He et al. supplementary movie 2(Video)
Video 780.3 KB