Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T06:53:23.785Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling smooth- and transitionally rough-wall turbulent channel flow by leveraging inner–outer interactions and principal component analysis

Published online by Cambridge University Press:  29 January 2019

Sicong Wu Open the ORCID record for Sicong Wu [Opens in a new window] ,
Kenneth T. Christensen Open the ORCID record for Kenneth T. Christensen [Opens in a new window]  and
Carlos Pantano Open the ORCID record for Carlos Pantano [Opens in a new window]
Sicong Wu*
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Kenneth T. Christensen
Affiliation:
Department of Aerospace and Mechanical Engineering and Civil and Environmental Engineering and Earth Sciences, University of Notre Dame, Notre Dame, IN 46556, USA International Institute for Carbon Neutral Energy Research (WPI-I2CNER), Kyushu University, Fukuoka 819-0385, Japan
Carlos Pantano
Affiliation:
Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of turbulent channel flow over rough surfaces, formed from hexagonally packed arrays of hemispheres on both walls, were performed at friction Reynolds numbers 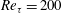$Re_{\unicode[STIX]{x1D70F}}=200$, 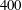$400$ and 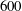$600$. The inner normalized roughness height 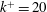$k^{+}=20$ was maintained for all Reynolds numbers, meaning all flows were classified as transitionally rough. The spacing between hemispheres was varied within $d/k=2$–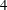$4$. The statistical properties of the rough-wall flows were contrasted against a complementary smooth-wall DNS at 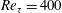$Re_{\unicode[STIX]{x1D70F}}=400$ and literature data at $Re_{\unicode[STIX]{x1D70F}}=2003$ revealing strong modifications of the near-wall turbulence, although the outer-layer structure was found to be qualitatively consistent with smooth-wall flow. Amplitude modulation (AM) analysis was used to explore the degree of interaction between the flow in the roughness sublayer and that of the outer layer utilizing all velocity components. This analysis revealed stronger modulation effects, compared to smooth-wall flow, on the near-wall small-scale fluctuations by the larger-scale structures residing in the outer layer irrespective of roughness arrangement and Reynolds number. A predictive inner–outer model based on these interactions, and exploiting principal component analysis (PCA), was developed to predict the statistics of higher-order moments of all velocity fluctuations, thus addressing modelling of anisotropic effects introduced by roughness. The results show excellent agreement between the predicted near-wall statistics up to fourth-order moments compared to the original statistics from the DNS, which highlights the utility of the PCA-enhanced AM model in generating physics-based predictions in both smooth- and rough-wall turbulence.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 407 - 453
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.10.1063/1.2717527Google Scholar
Agostini, L. & Leschziner, M. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28 (1), 015107.10.1063/1.4939712Google Scholar
Anderson, W. 2016 Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations. J. Fluid Mech. 789, 567–588.10.1017/jfm.2015.744Google Scholar
Anderson, W., Barros, J. M. & Christensen, K. T. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 748, 316–347.10.1017/jfm.2015.91Google Scholar
Ashrafian, A., Andersson, H. I. & Manhart, M. 2004 DNS of turbulent flow in a rod-roughened channel. Intl J. Heat Fluid Flow 25 (3), 373–383.10.1016/j.ijheatfluidflow.2004.02.004Google Scholar
Bailon-Cuba, J., Leonardi, S. & Castillo, L. 2009 Turbulent channel flow with 2d wedges of random height on one wall. Intl J. Heat Fluid Flow 30 (5), 1007–1015.10.1016/j.ijheatfluidflow.2009.03.017Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.10.1098/rsta.2006.1940Google Scholar
Barros, J. M. & Christensen, K. T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.10.1017/jfm.2014.218Google Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.10.1063/1.3589345Google Scholar
Birch, D. M. & Morrison, J. F. 2011 Similarity of the streamwise velocity component in very-rough-wall channel flow. J. Fluid Mech. 668, 174–201.10.1017/S0022112010004647Google Scholar
Bons, J. P., Taylor, R. P., McClain, S. T. & Rivir, R. B. 2001 The many faces of turbine surface roughness. In ASME Turbo Expo 2001: Power for Land, Sea, and Air, pp. V003T01A042–V003T01A042. American Society of Mechanical Engineers.Google Scholar
Bragg, M. B., Broeren, A. P. & Blumenthal, L. A. 2005 Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 41 (5), 323–362.10.1016/j.paerosci.2005.07.001Google Scholar
Burattini, P., Leonardi, S. & Orlandi, P. A. 2008 Comparison between experiments and direct numerical simulations in a channel flow with roughness on one wall. J. Fluid Mech. 600, 403–426.10.1017/S0022112008000657Google Scholar
Busse, A., Lutzner, M. & Sandham, N. D. 2015 Direct numerical simulation of turbulent flow over a rough surface based on a surface scan. Comput. Fluids 116, 129–147.10.1016/j.compfluid.2015.04.008Google Scholar
Busse, A., Thakkar, M. & Sandham, N. D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.10.1017/jfm.2016.680Google Scholar
Chan-Braun, C., García-Villalba, M. & Uhlmann, M. 2011 Force and torque acting on particles in a transitionally rough open-channel flow. J. Fluid Mech. 684, 441–474.10.1017/jfm.2011.311Google Scholar
Chatzikyriakou, D., Buongiorno, J., Caviezel, D. & Lakehal, D. 2015 DNS and LES of turbulent flow in a closed channel featuring a pattern of hemispherical roughness elements. Intl J. Heat Fluid Flow 53, 29–43.10.1016/j.ijheatfluidflow.2015.01.002Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104 (2), 229–259.10.1023/A:1016060103448Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.10.1017/S0022112093002575Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.10.1017/S0022112001003512Google Scholar
Chu, D. C. & Karniadakis, G. E. 1993 A direct numerical simulation of laminar and turbulent flow over riblet-mounted surfaces. J. Fluid Mech. 250, 1–42.10.1017/S0022112093001363Google Scholar
Coceal, O., Dobre, A., Thomas, T. G. & Belcher, S. E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.10.1017/S002211200700794XGoogle Scholar
Colebrook, C. F. & White, C. M. 1937 Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. A 161 (906), 367–381.Google Scholar
De Angelis, V., Lombardi, P. & Banerjee, S. 1997 Direct numerical simulation of turbulent flow over a wavy wall. Phys. Fluids 9 (8), 2429–2442.10.1063/1.869363Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.10.1146/annurev.fluid.32.1.519Google Scholar
Fischer, P. F.2010 nek tutorial. http://www.mcs.anl.gov/∼fischer/nek5000/.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2014 nek5000 Web page. https://nek5000.mcs.anl.gov/.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.10.1063/1.2757708Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.10.1063/1.1843135Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.10.1017/S0022112004002277Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.10.1017/S0022112002003270Google Scholar
Ghodke, C. D. & Apte, S. V. 2016 Dns study of particle-bed–turbulence interactions in an oscillatory wall-bounded flow. J. Fluid Mech. 792, 232–251.10.1017/jfm.2016.85Google Scholar
Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.10.1017/S0022112010003988Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.10.1063/1.2162185Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.10.1063/1.3005862Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.10.1017/S0022112006003946Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.10.1098/rsta.2006.1942Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.10.1017/S002211200600334XGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.10.1146/annurev.fluid.36.050802.122103Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.10.1017/S0022112008002747Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.10.1017/S0022112091002033Google Scholar
Johnson, R. A. & Wichern, D. W. 2014 Applied Multivariate Statistical Analysis. Prentice-Hall.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.10.1017/S0022112087000892Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.10.1063/1.869889Google Scholar
Krogstad, P.-Å., Andersson, H. I., Bakken, O. M. & Ashrafian, A. 2005 An experimental and numerical study of channel flow with rough walls. J. Fluid Mech. 530, 327–352.10.1017/S0022112005003824Google Scholar
Lee, J.-H., Sung, H.-J. & Krogstad, P.-A. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.10.1017/S0022112010005082Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to. J. Fluid Mech. 774, 395–415.10.1017/jfm.2015.268Google Scholar
Lee, S.-H. & Sung, H.-J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.10.1017/S0022112007006465Google Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.10.1017/S002211200999423XGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.10.1126/science.1188765Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.10.1017/S0022112009006946Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.10.1017/jfm.2011.216Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.10.1017/jfm.2012.508Google Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.10.1063/1.3267726Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2013 Wall-parallel stereo particle-image velocimetry measurements in the roughness sublayer of turbulent flow overlying highly irregular roughness. Phys. Fluids 25 (11), 115109.Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2010 Low-order representations of irregular surface roughness and their impact on a turbulent boundary layer. Phys. Fluids 22 (1), 015106.10.1063/1.3291076Google Scholar
Mejia-Alvarez, R., Wu, Y. & Christensen, K. T. 2014 Observations of meandering superstructures in the roughness sublayer of a turbulent boundary layer. Intl J. Heat Fluid Flow 48, 43–51.10.1016/j.ijheatfluidflow.2014.04.006Google Scholar
Monin, A. S. 1970 The atmospheric boundary layer. Annu. Rev. Fluid Mech. 2 (1), 225–250.10.1146/annurev.fl.02.010170.001301Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.10.1063/1.869966Google Scholar
Nagano, Y., Hattori, H. & Houra, T. 2004 DNS of velocity and thermal fields in turbulent channel flow with transverse-rib roughness. Intl J. Heat Fluid Flow 25 (3), 393–403.10.1016/j.ijheatfluidflow.2004.02.011Google Scholar
Nikuradse, J. 1933 Laws of flow in rough pipes. VDI Forschungsheft. Citeseer.Google Scholar
Orlandi, P. & Leonardi, S. 2008 Direct numerical simulation of three-dimensional turbulent rough channels: parameterization and flow physics. J. Fluid Mech. 606, 399–415.10.1017/S0022112008001985Google Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2006 Turbulent channel flow with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.10.1017/S0022112006000723Google Scholar
Pathikonda, G. & Christensen, K. T. 2017a Inner–outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2, 044603.10.1103/PhysRevFluids.2.044603Google Scholar
Pathikonda, G. & Christensen, K. T. 2017b Investigation of inner-outer interactions in a turbulent boundary layer using time-resolved PIV. In 10th Intl Symposium on Turbulence and Shear Flow Phenomena (TSFP10).Google Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. N. 1969 Rough wall turbulent boundary layers. J. Fluid Mech. 37 (02), 383–413.10.1017/S0022112069000619Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.10.1115/1.3119492Google Scholar
Roache, P. J. 1994 Perspective: a method for uniform reporting of grid refinement studies. Trans. ASME J. Fluids Engng 116 (3), 405–413.10.1115/1.2910291Google Scholar
Scotti, A. 2006 Direct numerical simulation of turbulent channel flows with boundary roughened with virtual sandpaper. Phys. Fluids 18 (3), 031701.10.1063/1.2183806Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.10.1090/qam/910462Google Scholar
Squire, D. T., Baars, W. J., Hutchins, N. & Marusic, I. 2016 Inner–outer interactions in rough-wall turbulence. J. Turbul. 17 (12), 1159–1178.10.1080/14685248.2016.1235278Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.10.1017/jfm.2014.132Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.10.1017/S0022112003005251Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vignoles, G. L., Lachaud, J., Aspa, Y. & Goyhénèche, J. 2009 Ablation of carbon-based materials: multiscale roughness modelling. Compos. Sci. Technol. 69 (9), 1470–1477.10.1016/j.compscitech.2008.09.019Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.10.1017/S0022112007008518Google Scholar
Willingham, D., Anderson, W., Christensen, K. T. & Barros, J. M. 2014 Turbulent boundary layer flow over transverse aerodynamic roughness transitions: Induced mixing and flow characterization. Phys. Fluids 26 (2), 025111.10.1063/1.4864105Google Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topography. Phys. Fluids 19 (8), 085108.10.1063/1.2741256Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.10.1017/S0022112010000960Google Scholar
Yin, G., Huang, W.-X. & Xu, C.-X. 2018 Prediction of near-wall turbulence using minimal flow unit. J. Fluid Mech. 841, 654–673.10.1017/jfm.2018.55Google Scholar
Yuan, J. & Piomelli, U. 2014 Roughness effects on the Reynolds stress budgets in near-wall turbulence. J. Fluid Mech. 760, R1.10.1017/jfm.2014.608Google Scholar