Published online by Cambridge University Press: 09 October 2013
We study the Reynolds-number scaling and the geometric self-similarity of a gain-based, low-rank approximation to turbulent channel flows, determined by the resolvent formulation of McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382), in order to obtain a description of the streamwise turbulence intensity from direct consideration of the Navier–Stokes equations. Under this formulation, the velocity field is decomposed into propagating waves (with single streamwise and spanwise wavelengths and wave speed) whose wall-normal shapes are determined from the principal singular function of the corresponding resolvent operator. Using the accepted scalings of the mean velocity in wall-bounded turbulent flows, we establish that the resolvent operator admits three classes of wave parameters that induce universal behaviour with Reynolds number in the low-rank model, and which are consistent with scalings proposed throughout the wall turbulence literature. In addition, it is shown that a necessary condition for geometrically self-similar resolvent modes is the presence of a logarithmic turbulent mean velocity. Under the practical assumption that the mean velocity consists of a logarithmic region, we identify the scalings that constitute hierarchies of self-similar modes that are parameterized by the critical wall-normal location where the speed of the mode equals the local turbulent mean velocity. For the rank-1 model subject to broadband forcing, the integrated streamwise energy density takes a universal form which is consistent with the dominant near-wall turbulent motions. When the shape of the forcing is optimized to enforce matching with results from direct numerical simulations at low turbulent Reynolds numbers, further similarity appears. Representation of these weight functions using similarity laws enables prediction of the Reynolds number and wall-normal variations of the streamwise energy intensity at high Reynolds numbers (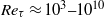 ${Re}_{\tau } \approx 1{0}^{3} {\unicode{x2013}} 1{0}^{10} $). Results from this low-rank model of the Navier–Stokes equations compare favourably with experimental results in the literature.
${Re}_{\tau } \approx 1{0}^{3} {\unicode{x2013}} 1{0}^{10} $). Results from this low-rank model of the Navier–Stokes equations compare favourably with experimental results in the literature.