Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-19T03:49:49.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Model reduction and mechanism for the vortex-induced vibrations of bluff bodies

Published online by Cambridge University Press:  22 August 2017

W. Yao  and
R. K. Jaiman Open the ORCID record for R. K. Jaiman [Opens in a new window]
W. Yao
Affiliation:
Department of Mechanical Engineering, National University Singapore, Singapore 119077, Singapore
R. K. Jaiman*
Affiliation:
Department of Mechanical Engineering, National University Singapore, Singapore 119077, Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an effective reduced-order model (ROM) technique to couple an incompressible flow with a transversely vibrating bluff body in a state-space format. The ROM of the unsteady wake flow is based on the Navier–Stokes equations and is constructed by means of an eigensystem realization algorithm (ERA). We investigate the underlying mechanism of vortex-induced vibration (VIV) of a circular cylinder at low Reynolds number via linear stability analysis. To understand the frequency lock-in mechanism and self-sustained VIV phenomenon, a systematic analysis is performed by examining the eigenvalue trajectories of the ERA-based ROM for a range of reduced oscillation frequency 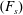$(F_{s})$, while maintaining fixed values of the Reynolds number (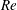$Re$) and mass ratio (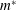$m^{\ast }$). The effects of the Reynolds number 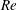$Re$, the mass ratio 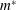$m^{\ast }$ and the rounding of a square cylinder are examined to generalize the proposed ERA-based ROM for the VIV lock-in analysis. The considered cylinder configurations are a basic square with sharp corners, a circle and three intermediate rounded squares, which are created by varying a single rounding parameter. The results show that the two frequency lock-in regimes, the so-called resonance and flutter, only exist when certain conditions are satisfied, and the regimes have a strong dependence on the shape of the bluff body, the Reynolds number and the mass ratio. In addition, the frequency lock-in during VIV of a square cylinder is found to be dominated by the resonance regime, without any coupled-mode flutter at low Reynolds number. To further discern the influence of geometry on the VIV lock-in mechanism, we consider the smooth curve geometry of an ellipse and two sharp corner geometries of forward triangle and diamond-shaped bluff bodies. While the ellipse and diamond geometries exhibit the flutter and mixed resonance–flutter regimes, the forward triangle undergoes only the flutter-induced lock-in for 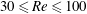$30\leqslant Re\leqslant 100$ at $m^{\ast }=10$. In the case of the forward triangle configuration, the ERA-based ROM accurately predicts the low-frequency galloping instability. We observe a kink in the amplitude response associated with 1:3 synchronization, whereby the forward triangular body oscillates at a single dominant frequency but the lift force has a frequency component at three times the body oscillation frequency. Finally, we present a stability phase diagram to summarize the VIV lock-in regimes of the five smooth-curve- and sharp-corner-based bluff bodies. These findings attempt to generalize our understanding of the VIV lock-in mechanism for bluff bodies at low Reynolds number. The proposed ERA-based ROM is found to be accurate, efficient and easy to use for the linear stability analysis of VIV, and it can have a profound impact on the development of control strategies for nonlinear vortex shedding and VIV.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 357 - 393
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, S. & Rowley, C. W. 2010 Feedback control of unstable steady states of flow past a flat plate using reduced-order estimators. J. Fluid Mech. 645, 447–478.CrossRefGoogle Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.CrossRefGoogle Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27 (5), 648–658.CrossRefGoogle Scholar
Blackburn, H. M. & Henderson, R. D. 1999 A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 385, 255–286.CrossRefGoogle Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14, 183–196.CrossRefGoogle Scholar
De Langre, E. 2006 Frequency lock-in is caused by coupled-mode flutter. J. Fluids Struct. 22 (6), 783–791.CrossRefGoogle Scholar
Dergham, G., Sipp, D., Robinet, J.-C. & Barbagallo, A. 2011 Model reduction for fluids using frequential snapshots. Phys. Fluids 23 (6), 064101.CrossRefGoogle Scholar
Flinois, T. L. B. & Morgans, A. S. 2016 Feedback control of unstable flows: a direct modelling approach using the eigensystem realisation algorithm. J. Fluid Mech. 793, 41–78.CrossRefGoogle Scholar
Flinois, T. L. B., Morgans, A. S. & Schmid, P. J. 2015 Projection-free approximate balanced truncation of large unstable systems. Phys. Rev. E 92 (2), 1–31.CrossRefGoogle ScholarPubMed
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
He, T., Zhou, D. & Bao, Y. 2012 Combined interface boundary condition method for fluid–rigid body interaction. Comput. Meth. Appl. Mech. Engng 223–224, 81–102.CrossRefGoogle Scholar
Ho, B. L. & Kalman, R. E. 1966 Effective construction of linear state-variable models from input–output functions. Regelungstechnik 14 (12), 545–585.Google Scholar
Jaiman, R. K., Geubelle, P., Loth, E. & Jiao, X. 2011 Transient fluid–structure interaction with non-matching spatial and temporal discretizations. Comput. Fluids 50, 120–135.CrossRefGoogle Scholar
Jaiman, R. K., Guan, M. Z. & Miyanawala, T. P. 2016a Partitioned iterative and dynamic subgrid-scale methods for freely vibrating square-section structures at high Reynolds number. Comput. Fluids 133, 1–22.CrossRefGoogle Scholar
Jaiman, R. K., Pillalamarri, N. R. & Guan, M. Z. 2016b A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow. Comput. Meth. Appl. Mech. Engng 301, 187–215.CrossRefGoogle Scholar
Jaiman, R. K., Sen, S. & Gurugubelli, P. S. 2015 A fully implicit combined field scheme for freely vibrating square cylinders with sharp and rounded corners. Comput. Fluids 112, 1–18.CrossRefGoogle Scholar
Juang, J.-N. & Pappa, R. S. 1985 An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. 8 (5), 620–627.CrossRefGoogle Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.CrossRefGoogle Scholar
Law, Y. Z. & Jaiman, R. K. 2017 Wake stabilization mechanism of low-drag suppression devices for vortex-induced vibration. J. Fluids Struct. 70, 428–449.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006 The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22, 857–864.CrossRefGoogle Scholar
Liu, B. & Jaiman, R. K. 2016 Interaction dynamics of gap flow and vortex-induced vibration side-by-side cylinder arrangement. Phys. Fluids 28 (12), 127103.CrossRefGoogle Scholar
Liu, J., Jaiman, R. K. & Gurugubelli, P. S. 2014 A stable second-order scheme for fluid–structure interaction with strong added-mass effects. J. Comput. Phys. 270, 687–710.CrossRefGoogle Scholar
Ma, Z., Ahuja, S. & Rowley, C. W. 2011 Reduced-order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 25 (1), 233–247.CrossRefGoogle Scholar
Mao, X. & Blackburn, H. M. 2014 The structure of primary instability modes in the steady wake and separation bubble of a square cylinder. Phys. Fluids 26 (7), 074103.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Meliga, P. & Chomaz, J. 2011 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. J. Fluid Mech. 671, 137–167.CrossRefGoogle Scholar
Mettot, C., Renac, F. & Sipp, D. 2014 Computation of eigenvalue sensitivity to base flow modifications in a discrete framework: application to open-loop control. J. Comput. Phys. 269, 234–258.CrossRefGoogle Scholar
Moore, B. C 1981 Principal component analysis in linear systems: controllability, observability, and model reduction. IEEE Trans. Autom. Control 26 (1), 17–32.CrossRefGoogle Scholar
Mysa, R. C., Kaboudian, A. & Jaiman, R. K. 2016 On the origin of wake-induced vibration in two tandem circular cylinders at low Reynolds number. J. Fluids Struct. 61, 76–98.CrossRefGoogle Scholar
Navrose & Mittal, S. 2016 Lock-in in vortex-induced vibration. J. Fluid Mech. 794, 565–594.CrossRefGoogle Scholar
Novotny, L. 2010 Strong coupling, energy splitting, and level crossings: a classical perspective. Am. J. Phys. 11 (78), 1199–1202.CrossRefGoogle Scholar
Park, D. & Yang, K. S. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Rowley, C. W. 2005 Model reduction for fluids, using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (3), 997–1013.CrossRefGoogle Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Shiels, D., Leonard, A. & Roshko, A. 2001 Flow-induced vibration of a circular cylinder at limiting structural parameters. J. Fluids Struct. 15, 3–21.CrossRefGoogle Scholar
Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex-shedding modes. J. Fluids Struct. 20 (8), 1085–1104.CrossRefGoogle Scholar
Tham, D. M. Y., Gurugubelli, P. S., Li, Z. & Jaiman, R. K. 2015 Freely vibrating circular cylinder in the vicinity of a stationary wall. J. Fluids Struct. 59, 103–128.CrossRefGoogle Scholar
Thompson, M. C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.CrossRefGoogle Scholar
Willcox, K. & Peraire, J. 2002 Balanced model reduction via the proper orthogonal decomposition. AIAA J. 40 (11), 2323–2330.CrossRefGoogle Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex-induced vibrations. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar
Yao, W. & Jaiman, R. K. 2016 A harmonic balance technique for the reduced-order computation of vortex-induced vibration. J. Fluids Struct. 65, 313–332.CrossRefGoogle Scholar
Yao, W. & Marques, S. 2015 Prediction of transonic limit-cycle oscillations using an aeroelastic harmonic balance method. AIAA J. 53 (7), 2040–2051.CrossRefGoogle Scholar
Yu, Y., Xie, F., Yan, H., Constantinides, Y., Oakley, O. & Karniadakis, G. E. 2015 Suppression of vortex-induced vibrations by fairings: a numerical study. J. Fluids Struct. 54, 679–700.CrossRefGoogle Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., Knig, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.CrossRefGoogle Scholar
Zhang, W., Li, X., Ye, Z. & Jiang, Y. 2015 Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers. J. Fluid Mech. 783, 72–102.CrossRefGoogle Scholar
Zhao, M., Cheng, L. & Zhou, T. 2013 Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number. Phys. Fluids 25 (2), 023603.Google Scholar