Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T07:28:10.311Z Has data issue: false hasContentIssue false
  • English
  • Français

Microemulsification from single laser-induced cavitation bubbles

Published online by Cambridge University Press:  14 December 2022

K Ashoke Raman Open the ORCID record for K Ashoke Raman [Opens in a new window] ,
Juan Manuel Rosselló Open the ORCID record for Juan Manuel Rosselló [Opens in a new window] ,
Hendrik Reese Open the ORCID record for Hendrik Reese [Opens in a new window]  and
Claus-Dieter Ohl Open the ORCID record for Claus-Dieter Ohl [Opens in a new window]
K Ashoke Raman*
Affiliation:
Department of Soft Matter, Institute of Physics, Otto-von-Guericke-Universität Magdeburg, Universitätsplatz 2, 39106 Magdeburg, Germany
Juan Manuel Rosselló
Affiliation:
Department of Soft Matter, Institute of Physics, Otto-von-Guericke-Universität Magdeburg, Universitätsplatz 2, 39106 Magdeburg, Germany
Hendrik Reese
Affiliation:
Department of Soft Matter, Institute of Physics, Otto-von-Guericke-Universität Magdeburg, Universitätsplatz 2, 39106 Magdeburg, Germany
Claus-Dieter Ohl
Affiliation:
Department of Soft Matter, Institute of Physics, Otto-von-Guericke-Universität Magdeburg, Universitätsplatz 2, 39106 Magdeburg, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

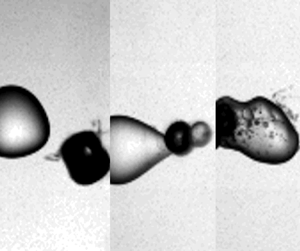
We study the interaction between a laser-induced cavitation bubble and a submillimetre-sized water droplet submerged in silicone oil. High-speed imaging reveals the pathways through which droplet fragmentation occurs and three distinct regimes of bubble–droplet interaction are identified: deformation, external emulsification and internal emulsification. We have observed that during the bubble collapse, the droplet elongates towards the bubble, which acts as a flow sink pulling on the droplet. For silicone oils with higher viscosity, the droplet jets into the cavitation bubble and forms a satellite water droplet in the continuous oil phase. In contrast, for lower-viscosity oils, the droplet encapsulates the collapsing bubble as it jets inside and undergoes multiple cycles of expansion and collapse. These internal bubble collapses create tiny oil droplets inside the parent water droplet. The kinematic viscosity of the silicone oil, maximum bubble diameter and centre-to-centre distance between the bubble and the droplet are varied. The regimes are separated in a parameter space set up by the non-dimensional distance and a cavitation Reynolds number.

JFM classification

Drops and Bubbles: Drops Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Cavitation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A27
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Avila, S.R.G. & Ohl, C-D 2016 Fragmentation of acoustically levitating droplets by laser-induced cavitation bubbles. J. Fluid Mech. 805, 551–576.CrossRefGoogle Scholar
Benjamin, T.B. & Ellis, A.T. 1966 The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Phil. Trans. R. Soc. Lond. Ser. A, Math. Phys. Sci. 260, 221–240.Google Scholar
Bentley, B.J. & Leal, L.G. 1986 An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech. 167, 241–283.CrossRefGoogle Scholar
Brennen, C.E. 2014 Cavitation and Bubble Dynamics. Cambridge University Press.Google Scholar
Canselier, J.P., Delmas, H., Wilhelm, A.M. & Abismail, B. 2002 Ultrasound emulsification–an overview. J. Dispers. Sci. Technol. 23 (1-3), 333–349.CrossRefGoogle Scholar
Cao, X.K., Sun, Z.G., Li, W.F., Liu, H.F. & Yu, Z.H. 2007 A new breakup regime of liquid drops identified in a continuous and uniform air jet flow. Phys. Fluids 19 (5), 057103.CrossRefGoogle Scholar
Church, C.C. 1995 The effects of an elastic solid surface layer on the radial pulsations of gas bubbles. J. Acoust. Soc. Am. 97 (3), 1510–1521.CrossRefGoogle Scholar
Cristini, V., Guido, S., Alfani, A., Bławzdziewicz, J. & Loewenberg, M. 2003 Drop breakup and fragment size distribution in shear flow. J. Rheol. 47 (5), 1283–1298.CrossRefGoogle Scholar
Dijkink, R. & Ohl, C-D 2008 Measurement of cavitation induced wall shear stress. Appl. Phys. Lett. 93 (25), 254107.CrossRefGoogle Scholar
Evangelio, A., Campo-Cortés, F. & Gordillo, J.M. 2016 Simple and double microemulsions via the capillary breakup of highly stretched liquid jets. J. Fluid Mech. 804, 550–577.CrossRefGoogle Scholar
García-Geijo, P, Quintero, E.S., Riboux, G & Gordillo, J.M. 2021 Spreading and splashing of drops impacting rough substrates. J. Fluid Mech. 917, A50.CrossRefGoogle Scholar
Gelderblom, H., Lhuissier, H., Klein, A.L., Bouwhuis, W., Lohse, D., Villermaux, E. & Snoeijer, J.H. 2016 Drop deformation by laser-pulse impact. J. Fluid Mech. 794, 676–699.CrossRefGoogle Scholar
Grigoryev, S.Y., et al. 2018 Expansion and fragmentation of a liquid-metal droplet by a short laser pulse. Phys. Rev. Appl. 10 (6), 064009.CrossRefGoogle Scholar
Guildenbecher, D.R., López-Rivera, C. & Sojka, P.E. 2009 Secondary atomization. Exp. Fluids 46 (3), 371–402.CrossRefGoogle Scholar
Han, J. & Tryggvason, G. 2001 Secondary breakup of axisymmetric liquid drops. II. Impulsive acceleration. Phys. Fluids 13 (6), 1554–1565.CrossRefGoogle Scholar
Han, R., Zhang, A., Tan, S. & Li, S. 2022 Interaction of cavitation bubbles with the interface of two immiscible fluids on multiple time scales. J. Fluid Mech. 932, A8.CrossRefGoogle Scholar
Hijo, A.A.C.T., Guinosa, R.E. & Silva, E.K. 2022 Ultrasound emulsification energy strategies impact the encapsulation efficiency of essential oils in colloidal systems. J. Mol. Liq. 358, 119179.CrossRefGoogle Scholar
Hirahara, H. & Kawahashi, M. 1992 Experimental investigation of viscous effects upon a breakup of droplets in high-speed air flow. Exp. Fluids 13 (6), 423–428.CrossRefGoogle Scholar
Hsiang, L.P. & Faeth, G.M. 1995 Drop deformation and breakup due to shock wave and steady disturbances. Intl J. Multiphase Flow 21 (4), 545–560.CrossRefGoogle Scholar
Jalaal, M. & Mehravaran, K. 2012 Fragmentation of falling liquid droplets in bag breakup mode. Intl J. Multiphase Flow 47, 115–132.CrossRefGoogle Scholar
Ji, Y., Bellettre, J., Montillet, A. & Massoli, P. 2020 Fast oil-in-water emulsification in microchannel using head-on impinging configuration: effect of swirl motion. Intl J. Multiphase Flow 131, 103402.CrossRefGoogle Scholar
Joseph, D.D., Belanger, J. & Beavers, G.S. 1999 Breakup of a liquid drop suddenly exposed to a high-speed airstream. Intl J. Multiphase Flow 25 (6–7), 1263–1303.CrossRefGoogle Scholar
Josserand, C. & Thoroddsen, S.T 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48 (1), 365–391.CrossRefGoogle Scholar
Kaci, M., Meziani, S., Arab-Tehrany, E., Gillet, G., Desjardins-Lavisse, I. & Desobry, S. 2014 Emulsification by high frequency ultrasound using piezoelectric transducer: formation and stability of emulsifier free emulsion. Ultrason. Sonochem. 21 (3), 1010–1017.CrossRefGoogle ScholarPubMed
Kamiya, T., Asahara, M., Yada, T., Mizuno, K. & Miyasaka, T. 2022 Study on characteristics of fragment size distribution generated via droplet breakup by high-speed gas flow. Phys. Fluids 34 (1), 012118.CrossRefGoogle Scholar
Kim, S. & Dabiri, S. 2017 Transient dynamics of eccentric double emulsion droplets in a simple shear flow. Phys. Rev. Fluids 2 (10), 104305.CrossRefGoogle Scholar
Klein, A.L., Kurilovich, D., Lhuissier, H., Versolato, O.O., Lohse, D., Villermaux, E. & Gelderblom, H. 2020 Drop fragmentation by laser-pulse impact. J. Fluid Mech. 893, A7.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers. C. R. Acad. Sci. URSS 30, 301–305.Google Scholar
Kulkarni, V. & Sojka, P.E. 2014 Bag breakup of low viscosity drops in the presence of a continuous air jet. Phys. Fluids 26 (7), 072103.CrossRefGoogle Scholar
Li, M.K. & Fogler, H.S. 1978 a Acoustic emulsification. Part 1. The instability of the oil-water interface to form the initial droplets. J. Fluid Mech. 88 (3), 499–511.CrossRefGoogle Scholar
Li, M.K. & Fogler, H.S. 1978 b Acoustic emulsification. Part 2. Breakup of the large primary oil droplets in a water medium. J. Fluid Mech. 88 (3), 513–528.CrossRefGoogle Scholar
Li, W., Leong, T.S.H., Kumar, M.A. & Martin, G.J.O. 2018 A study of the effectiveness and energy efficiency of ultrasonic emulsification. Phys. Chem. Chem. Phys. 20 (1), 86–96.CrossRefGoogle Scholar
Lindau, O. & Lauterborn, W. 2003 Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 479, 327–348.CrossRefGoogle Scholar
Liu, X., Liu, Z., Jiang, S., Zhu, C., Ma, Y. & Fu, T. 2022 Formation of droplets of shear-thinning non-newtonian fluids in a step-emulsification microdevice. AIChE J. 68 (1), e17395.CrossRefGoogle Scholar
Liu, Z. & Reitz, R.D. 1997 An analysis of the distortion and breakup mechanisms of high speed liquid drops. Intl J. Multiphase Flow 23 (4), 631–650.CrossRefGoogle Scholar
Liu, H., Zhang, J., Ba, Y., Wang, N. & Wu, L. 2020 Modelling a surfactant-covered droplet on a solid surface in three-dimensional shear flow. J. Fluid Mech. 897, A33.CrossRefGoogle Scholar
OpenFOAM-v2006 2020 Available at: https://www.openfoam.com/download/release-history.Google Scholar
Orthaber, U., Zevnik, J., Dular, M., et al. 2020 Cavitation bubble collapse in a vicinity of a liquid-liquid interface–basic research into emulsification process. Ultrason. Sonochem. 68, 105224.CrossRefGoogle Scholar
Perdih, T.S., Zupanc, M. & Dular, M. 2019 Revision of the mechanisms behind oil-water (o/w) emulsion preparation by ultrasound and cavitation. Ultrason. Sonochem. 51, 298–304.CrossRefGoogle Scholar
Perrin, L., Desobry-Banon, S., Gillet, G. & Desobry, S. 2022 Review of high-frequency ultrasounds emulsification methods and oil/water interfacial organization in absence of any kind of stabilizer. Foods 11 (15), 2194.CrossRefGoogle ScholarPubMed
Rallison, J.M. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 16 (1), 45–66.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the pressure developed in a liquid during the collapse of a spherical cavity. Lond. Edinb. Dublin Philos. Mag. J. Sci., Ser. 6 34, 94–98.CrossRefGoogle Scholar
Ren, Z., Li, X., Ma, F., Zhang, Y., Hu, W., Khan, M.Z.H. & Liu, X. 2022 Oil-in-water emulsions prepared using high-pressure homogenisation with dioscorea opposita mucilage and food-grade polysaccharides: guar gum, xanthan gum, and pectin. Lebensmittel-Wissensch. Technol. 162, 113468.CrossRefGoogle Scholar
Renardy, Y.Y. & Cristini, V. 2001 Scalings for fragments produced from drop breakup in shear flow with inertia. Phys. Fluids 13 (8), 2161–2164.CrossRefGoogle Scholar
Rosselló, J.M., Lauterborn, W., Koch, M., Wilken, T., Kurz, T. & Mettin, R. 2018 Acoustically induced bubble jets. Phys. Fluids 30 (12), 122004.CrossRefGoogle Scholar
Schultz, S., Wagner, G., Urban, K. & Ulrich, J. 2004 High-pressure homogenization as a process for emulsion formation. Chem. Engng Technol.: Ind. Chem.-Plant Equip.-Process Engng-Biotechnol. 27 (4), 361–368.CrossRefGoogle Scholar
Sharma, S., Chandra, N.K., Basu, S. & Kumar, A. 2022 Advances in droplet aerobreakup. Eur. Phys. J. Spec. Topics 1–15.Google Scholar
Shraiber, A.A., Podvysotsky, A.M. & Dubrovsky, V.V. 1996 Deformation and breakup of drops by aerodynamic forces. Atomiz. Sprays 6 (6), 667–692.CrossRefGoogle Scholar
Singh, N. & Narsimhan, V. 2022 Numerical investigation of the effect of surface viscosity on droplet breakup and relaxation under axisymmetric extensional flow. J. Fluid Mech. 946, A24.CrossRefGoogle Scholar
Soto, D., Girard, H.-L., Le Helloco, A., Binder, T., Quéré, D. & Varanasi, K.K 2018 Droplet fragmentation using a mesh. Phys. Rev. Fluids 3 (8), 083602.CrossRefGoogle Scholar
Stone, H.A., Bentley, B.J. & Leal, L.G. 1986 An experimental study of transient effects in the breakup of viscous drops. J. Fluid Mech. 173, 131–158.CrossRefGoogle Scholar
Stone, H.A. & Leal, L.G. 1990 Breakup of concentric double emulsion droplets in linear flows. J. Fluid Mech. 211, 123–156.CrossRefGoogle Scholar
Taha, A., Ahmed, E., Ismaiel, A., Kumar, M.A., Xu, X., Pan, S. & Hu, H. 2020 Ultrasonic emulsification: an overview on the preparation of different emulsifiers-stabilized emulsions. Trends Food Sci. Technol. 105, 363–377.CrossRefGoogle Scholar
Taylor, G.I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. Ser. A, Contain. Papers Math. Phys. Character 146 (858), 501–523.Google Scholar
Theofanous, T.G. & Li, G.J. 2008 On the physics of aerobreakup. Phys. Fluids 20 (5), 052103.CrossRefGoogle Scholar
Thoroddsen, S.T., Takehara, K., Etoh, T.G. & Ohl, C-D 2009 Spray and microjets produced by focusing a laser pulse into a hemispherical drop. Phys. Fluids 21 (11), 112101.CrossRefGoogle Scholar
Tomita, Y., Robinson, P.B., Tong, R.P. & Blake, J.R. 2002 Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 466, 259–283.CrossRefGoogle Scholar
Vankova, N., Tcholakova, S., Denkov, N.D., Ivanov, I.B., Vulchev, V.D. & Danner, T. 2007 Emulsification in turbulent flow: 1. Mean and maximum drop diameters in inertial and viscous regimes. J. Colloid Interface Sci. 312 (2), 363–380.CrossRefGoogle ScholarPubMed
Villermaux, E. & Bossa, B. 2011 Drop fragmentation on impact. J. Fluid Mech. 668, 412–435.CrossRefGoogle Scholar
Wang, Y & Bourouiba, L 2018 Unsteady sheet fragmentation: droplet sizes and speeds. J. Fluid Mech. 848, 946–967.CrossRefGoogle Scholar
Wang, N., Semprebon, C., Liu, H., Zhang, C. & Kusumaatmaja, H. 2020 Modelling double emulsion formation in planar flow-focusing microchannels. J. Fluid Mech. 895, A22.CrossRefGoogle Scholar
Yamamoto, T. & Komarov, S.V. 2020 Liquid jet directionality and droplet behavior during emulsification of two liquids due to acoustic cavitation. Ultrason. Sonochem. 62, 104874.CrossRefGoogle ScholarPubMed
Yamamoto, T., Matsutaka, R. & Komarov, S.V 2021 High-speed imaging of ultrasonic emulsification using a water-gallium system. Ultrason. Sonochem. 71, 105387.CrossRefGoogle ScholarPubMed
Yarin, A.L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing$\ldots$. Annu. Rev. Fluid Mech. 38, 159–192.CrossRefGoogle Scholar
Zhao, S., Dong, Z., Yao, C., Wen, Z., Chen, G. & Yuan, Q. 2018 Liquid–liquid two-phase flow in ultrasonic microreactors: cavitation, emulsification, and mass transfer enhancement. AIChE J. 64 (4), 1412–1423.CrossRefGoogle Scholar
Zhou, L., Zhang, W., Wang, J., Zhang, R. & Zhang, J. 2022 Comparison of oil-in-water emulsions prepared by ultrasound, high-pressure homogenization and high-speed homogenization. Ultrason. Sonochem. 82, 105885.CrossRefGoogle ScholarPubMed