Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T00:15:37.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Melting processes of phase change materials in a horizontally placed rectangular cavity

Published online by Cambridge University Press:  26 October 2022

Min Li ,
Zhenjun Jiao  and
Pan Jia Open the ORCID record for Pan Jia [Opens in a new window]
Min Li
Affiliation:
School of Science, Harbin Institute of Technology, Shenzhen 518055, PR China
Zhenjun Jiao
Affiliation:
School of Science, Harbin Institute of Technology, Shenzhen 518055, PR China
Pan Jia*
Affiliation:
School of Science, Harbin Institute of Technology, Shenzhen 518055, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

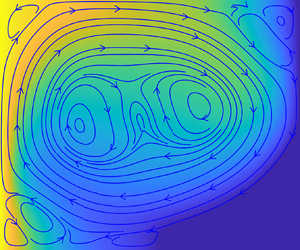
This paper revisits the melting process of phase change materials (PCMs) enclosed in a horizontally placed rectangular cavity, with isothermal and adiabatic conditions subjected to the vertical and horizontal walls, respectively. First, numerical simulations based on an improved lattice Boltzmann method are conducted to illustrate and to inform the theoretical modelling. It is shown that, compared with the traditional two-stage conduction–convection melting description, it is more reasonable to include a third stage in terms of the heat transfer behaviour. During the third stage, the remnant solid PCM is located in the corner formed by the cold and bottom walls of the cavity, and an increasing part of the input energy will be transferred directly out of the cavity without compensating for the melting latent heat, thus inducing a continuously decreasing melting rate until the end of the melting process. Then theoretical predictions are derived piecewise for the melted liquid fraction during the entire melting process, and the corresponding transitions between two successive stages are also discussed. The results are validated successfully via the available experimental and numerical data in the literature, and could guide the design and operation of latent heat storage systems.

JFM classification

Phase change: Solidification/melting Convection: Convection in cavities
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 950 , 10 November 2022 , A34
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahmad, M., Bontemps, A., Sallée, H. & Quenard, D. 2006 Experimental investigation and computer simulation of thermal behaviour of wallboards containing a phase change material. Energy Build. 38 (4), 357–366.CrossRefGoogle Scholar
Alboussiere, T., Deguen, R. & Melzani, M. 2010 Melting-induced stratification above the Earth's inner core due to convective translation. Nature 466 (7307), 744–747.CrossRefGoogle ScholarPubMed
Baby, R. & Balaji, C. 2013 Experimental investigations on thermal performance enhancement and effect of orientation on porous matrix filled PCM based heat sink. Intl Commun. Heat Mass Transfer 46, 27–30.CrossRefGoogle Scholar
Baehr, H.D. & Stephan, K. 2011 Heat and Mass Transfer. Springer Science & Business Media.CrossRefGoogle Scholar
Bareiss, M & Beer, H 1984 Experimental investigation of melting heat transfer with regard to different geometric arrangements. Intl Commun. Heat Mass Transfer 11 (4), 323–333.CrossRefGoogle Scholar
Behbahan, A.S., Noghrehabadi, A., Wong, C.P., Pop, I. & Behbahani-Nejad, M. 2019 Investigation of enclosure aspect ratio effects on melting heat transfer characteristics of metal foam/phase change material composites. Intl J. Numer. Meth. Heat Fluid Flow 29, 2994–3011.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50 (1), 269.CrossRefGoogle ScholarPubMed
Bénard, C, Gobin, D & Martinez, F 1985 Melting in rectangular enclosures: experiments and numerical simulations. Trans. ASME: J. Heat Transfer 107 (4), 794–803.CrossRefGoogle Scholar
Bertrand, O., et al. 1999 Melting driven by natural convection a comparison exercise: first results. Intl J. Therm. Sci. 38 (1), 5–26.CrossRefGoogle Scholar
Boger, D.V. & Westwater, J.W. 1967 Effect of buoyancy on the melting and freezing process. J. Heat Transfer 89 (1), 81–89.Google Scholar
Brent, A.D., Voller, V.R & Reid, K.T.J 1988 Enthalpy-porosity technique for modeling convection–diffusion phase change: application to the melting of a pure metal. Numer. Heat Transfer, A Applics 13 (3), 297–318.Google Scholar
Campbell, T.A. & Koster, J.N. 1994 Visualization of liquid–solid interface morphologies in gallium subject to natural convection. J. Cryst. Growth 140 (3-4), 414–425.CrossRefGoogle Scholar
Chakraborty, S. & Chatterjee, D. 2007 An enthalpy-based hybrid lattice-Boltzmann method for modelling solid–liquid phase transition in the presence of convective transport. J. Fluid Mech. 592, 155–175.CrossRefGoogle Scholar
Dhaidan, N.S & Khodadadi, J.M. 2015 Melting and convection of phase change materials in different shape containers: a review. Renew. Sustain. Energy Rev. 43, 449–477.CrossRefGoogle Scholar
Du, Y., Yuan, Y., Jia, D., Cheng, B. & Mao, J. 2007 Experimental investigation on melting characteristics of ethanolamine–water binary mixture used as PCM. Intl Commun. Heat Mass Transfer 34 (9–10), 1056–1063.Google Scholar
Duan, J., Xiong, Y. & Yang, D. 2019 On the melting process of the phase change material in horizontal rectangular enclosures. Energies 12 (16), 3100.CrossRefGoogle Scholar
Dutil, Y., Rousse, D.R., Salah, N.B., Lassue, S. & Zalewski, L. 2011 A review on phase-change materials: mathematical modeling and simulations. Renew. Sustain. Energy Rev. 15 (1), 112–130.CrossRefGoogle Scholar
El Qarnia, H, Draoui, A & Lakhal, E.K. 2013 Computation of melting with natural convection inside a rectangular enclosure heated by discrete protruding heat sources. Appl. Math. Model. 37 (6), 3968–3981.CrossRefGoogle Scholar
Esfahani, B.R., Hirata, S.C, Berti, S. & Calzavarini, E. 2018 Basal melting driven by turbulent thermal convection. Phys. Rev. Fluids 3 (5), 053501.CrossRefGoogle Scholar
Faden, M., Linhardt, C., Höhlein, S., König-Haagen, A. & Brüggemann, D. 2019 Velocity field and phase boundary measurements during melting of n-octadecane in a cubical test cell. Intl J. Heat Mass Transfer 135, 104–114.CrossRefGoogle Scholar
Favier, B., Purseed, J. & Duchemin, L. 2019 Rayleigh–Bénard convection with a melting boundary. J. Fluid Mech. 858, 437–473.CrossRefGoogle Scholar
Gadgil, A & Gobin, D 1984 Analysis of two-dimensional melting in rectangular enclosures in presence of convection. Trans. ASME: J. Heat Transfer 106 (1), 20–26.CrossRefGoogle Scholar
Garg, H.P., Mullick, S.C. & Bhargava, V.K 2012 Solar Thermal Energy Storage. Springer Science & Business Media.Google Scholar
Gau, C & Viskanta, R 1985 Effect of natural convection on solidification from above and melting from below of a pure metal. Intl J. Heat Mass Transfer 28 (3), 573–587.CrossRefGoogle Scholar
Gau, C. & Viskanta, R 1986 Melting and solidification of a pure metal on a vertical wall. Trans. ASME: J. Heat Transfer 108 (1), 174–181.CrossRefGoogle Scholar
Gong, Z.-X., Devahastin, S. & Mujumdar, A.S 1999 Enhanced heat transfer in free convection-dominated melting in a rectangular cavity with an isothermal vertical wall. Appl. Therm. Engng 19 (12), 1237–1251.CrossRefGoogle Scholar
Hamdan, M.A & Al-Hinti, I. 2004 Analysis of heat transfer during the melting of a phase-change material. Appl. Therm. Engng 24 (13), 1935–1944.CrossRefGoogle Scholar
Hamad, F.A., Egelle, E., Cummings, K. & Russell, P. 2017 Investigation of the melting process of polyethylene glycol 1500 (PEG 1500) in a rectagular enclosure. Intl J. Heat Mass Transfer 114, 1234–1247.CrossRefGoogle Scholar
Hamad, F.A., Egelle, E., Gooneratne, S. & Russell, P. 2021 The effect of aspect ratio on PCM melting behaviour in rectangular enclosure. Intl J. Sustain. Engng 14 (5), 1251–1268.CrossRefGoogle Scholar
Hamdan, M.A. & Elwerr, F.A. 1996 Thermal energy storage using a phase change material. Solar Energy 56 (2), 183–189.CrossRefGoogle Scholar
Hannoun, N., Alexiades, V. & Mai, T.Z. 2003 Resolving the controversy over tin and gallium melting in a rectangular cavity heated from the side. Numer. Heat Transfer: B: Fundam. 44 (3), 253–276.CrossRefGoogle Scholar
Hasan, M.S. & Saha, S.K 2021 Evolution of solid–liquid interface in bottom heated cavity for low Prandtl number using lattice Boltzmann method. Phys. Fluids 33 (5), 057102.CrossRefGoogle Scholar
He, Y., Qi, C., Hu, Y., Qin, B., Li, F. & Ding, Y. 2011 Lattice Boltzmann simulation of alumina–water nanofluid in a square cavity. Nanoscale Res. Lett. 6 (1), 184.CrossRefGoogle Scholar
Ho, C-J & Viskanta, R 1984 Heat transfer during melting from an isothermal vertical wall. Trans. ASME: J. Heat Transfer 106 (1), 12–19.CrossRefGoogle Scholar
Huang, R., Wu, H. & Cheng, P. 2013 A new lattice Boltzmann model for solid–liquid phase change. Intl J. Heat Mass Transfer 59, 295–301.CrossRefGoogle Scholar
Jany, P. & Bejan, A. 1988 Scaling theory of melting with natural convection in an enclosure. Intl J. Heat Mass Transfer 31 (6), 1221–1235.CrossRefGoogle Scholar
Jourabian, M., Farhadi, M. & Darzi, A.A.R. 2013 Convection-dominated melting of phase change material in partially heated cavity: lattice Boltzmann study. Heat Mass Transfer 49 (4), 555–565.CrossRefGoogle Scholar
Kadri, S., Dhifaoui, B., Dutil, Y., Jabrallah, S.B. & Rousse, D.R 2015 Large-scale experimental study of a phase change material: shape identification for the solid–liquid interface. Intl J. Thermophys. 36 (10), 2897–2915.CrossRefGoogle Scholar
Kakac, S., Aung, W. & Viskanta, R. 1985 Natural Convection: Fundamentals and Applications. Hemisphere.Google Scholar
Kamkari, B., Shokouhmand, H. & Bruno, F. 2014 Experimental investigation of the effect of inclination angle on convection-driven melting of phase change material in a rectangular enclosure. Intl J. Heat Mass Transfer 72, 186–200.CrossRefGoogle Scholar
Kim, T.Y., Hyun, B.-S., Lee, J.-J. & Rhee, J. 2013 Numerical study of the spacecraft thermal control hardware combining solid–liquid phase change material and a heat pipe. Aerospace Sci. Technol. 27 (1), 10–16.CrossRefGoogle Scholar
Kim, M.C., Lee, D.W. & Choi, C.K. 2008 Onset of buoyancy-driven convection in melting from below. Korean J. Chem. Engng 25 (6), 1239–1244.CrossRefGoogle Scholar
Lee, K.O., Medina, M.A, Raith, E. & Sun, X. 2015 Assessing the integration of a thin phase change material (PCM) layer in a residential building wall for heat transfer reduction and management. Appl. Energy 137, 699–706.CrossRefGoogle Scholar
Levin, P.P, Shitzer, A. & Hetsroni, G. 2013 Numerical optimization of a PCM-based heat sink with internal fins. Intl J. Heat Mass Transfer 61, 638–645.CrossRefGoogle Scholar
Li, Z., Yang, M. & Zhang, Y. 2014 A hybrid lattice Boltzmann and finite-volume method for melting with convection. Numer. Heat Transfer, B: Fundam. 66 (4), 307–325.CrossRefGoogle Scholar
Luo, K., Yao, F.-J., Yi, H.-L. & Tan, H.-P. 2015 Lattice Boltzmann simulation of convection melting in complex heat storage systems filled with phase change materials. Appl. Therm. Engng 86, 238–250.CrossRefGoogle Scholar
Nazir, H., Batool, M., Osorio, F.J.B.olivar, Isaza-Ruiz, M., Xu, X., Vignarooban, K, Phelan, P., Kannan, A.M, et al. 2019 Recent developments in phase change materials for energy storage applications: a review. Intl J. Heat Mass Transfer 129, 491–523.CrossRefGoogle Scholar
Ng, C.S., Ooi, A., Lohse, D. & Chung, D. 2015 Vertical natural convection: application of the unifying theory of thermal convection. J. Fluid Mech. 764, 349–361.CrossRefGoogle Scholar
Purseed, J., Favier, B., Duchemin, L. & Hester, E.W 2020 Bistability in Rayleigh–Bénard convection with a melting boundary. Phys. Rev. Fluids 5 (2), 023501.CrossRefGoogle Scholar
Rakotondrandisa, A., Danaila, I. & Danaila, L. 2019 Numerical modelling of a melting-solidification cycle of a phase-change material with complete or partial melting. Intl J. Heat Fluid Flow 76, 57–71.CrossRefGoogle Scholar
Ramakrishnan, S., Wang, X., Alam, M., Sanjayan, J. & Wilson, J. 2016 Parametric analysis for performance enhancement of phase change materials in naturally ventilated buildings. Energy Build. 124, 35–45.CrossRefGoogle Scholar
Rui, Z., Li, J., Ma, J., Cai, H., Nie, B. & Peng, H. 2020 Comparative study on natural convection melting in square cavity using lattice Boltzmann method. Results Phys. 18, 103274.CrossRefGoogle Scholar
Sarier, N. & Onder, E. 2012 Organic phase change materials and their textile applications: an overview. Thermochim. Acta 540, 7–60.CrossRefGoogle Scholar
Scheel, J.D & Schumacher, Jörg 2014 Local boundary layer scales in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 758, 344–373.CrossRefGoogle Scholar
Sharifi, N., Robak, C.W, Bergman, T.L & Faghri, A. 2013 Three-dimensional PCM melting in a vertical cylindrical enclosure including the effects of tilting. Intl J. Heat Mass Transfer 65, 798–806.CrossRefGoogle Scholar
Sharma, A., Tyagi, V.V., Chen, C.R. & Buddhi, D. 2009 Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 13 (2), 318–345.CrossRefGoogle Scholar
Shishkina, O. 2016 Momentum and heat transport scalings in laminar vertical convection. Phys. Rev. E 93 (5), 051102.CrossRefGoogle ScholarPubMed
Shokouhmand, H. & Kamkari, B. 2013 Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit. Exp. Therm. Fluid Sci. 50, 201–212.CrossRefGoogle Scholar
Swanson, T.D & Birur, G.C 2003 NASA thermal control technologies for robotic spacecraft. Appl. Therm. Engng 23 (9), 1055–1065.CrossRefGoogle Scholar
Takeshita, T., Segawa, T., Glazier, J.A & Sano, M. 1996 Thermal turbulence in mercury. Phys. Rev. Lett. 76 (9), 1465.CrossRefGoogle ScholarPubMed
Verzicco, R & Camussi, R 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.CrossRefGoogle Scholar
Wang, Q., Liu, H.-R., Verzicco, R., Shishkina, O. & Lohse, D. 2021 Regime transitions in thermally driven high-Rayleigh number vertical convection. J. Fluid Mech. 917, A6.CrossRefGoogle Scholar
Wang, S., Faghri, A. & Bergman, T.L 2010 A comprehensive numerical model for melting with natural convection. Intl J. Heat Mass Transfer 53 (9-10), 1986–2000.CrossRefGoogle Scholar
Wang, Y, Amiri, A & Vafai, K 1999 An experimental investigation of the melting process in a rectangular enclosure. Intl J. Heat Mass Transfer 42 (19), 3659–3672.CrossRefGoogle Scholar
Wang, Z., Calzavarini, E. & Sun, C. 2021 a Equilibrium states of the ice–water front in a differentially heated rectangular cell (a). Europhys. Lett. 135 (5), 54001.CrossRefGoogle Scholar
Wang, Z., Calzavarini, E., Sun, C. & Toschi, F. 2021 b How the growth of ice depends on the fluid dynamics underneath. Proc. Natl Acad. Sci. 118 (10), e2012870118.Google ScholarPubMed
Wang, Z., Jiang, L., Du, Y., Sun, C. & Calzavarini, E. 2021 c Ice front shaping by upward convective current. Phys. Rev. Fluids 6 (9), L091501.CrossRefGoogle Scholar
Webb, B.W. & Viskanta, R 1986 Analysis of heat transfer during melting of a pure metal from an isothermal vertical wall. Numer. Heat Transfer, A: Applics. 9 (5), 539–558.Google Scholar
Wolff, F & Viskanta, R 1988 Solidification of a pure metal at a vertical wall in the presence of liquid superheat. Intl J. Heat Mass Transfer 31 (8), 1735–1744.CrossRefGoogle Scholar
Yang, X., Guo, Z., Liu, Y., Jin, L. & He, Y.-L. 2019 Effect of inclination on the thermal response of composite phase change materials for thermal energy storage. Appl. Energy 238, 22–33.CrossRefGoogle Scholar
Zhang, Y., Chen, Z., Wang, Q. & Wu, Q. 1993 Melting in an enclosure with discrete heating at a constant rate. Exp. Therm. Fluid Sci. 6 (2), 196–201.CrossRefGoogle Scholar
Zhou, Q., Stevens, R.J.A.M, Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104 (10), 104301.CrossRefGoogle ScholarPubMed
Zhou, D., Zhao, C.-Y. & Tian, Y. 2012 Review on thermal energy storage with phase change materials (PCMs) in building applications. Appl. Energy 92, 593–605.CrossRefGoogle Scholar