Article contents
Mechanisms of flow tripping by discrete roughness elements in a swept-wing boundary layer
Published online by Cambridge University Press: 28 April 2016
Abstract
The effects of a spanwise row of finite-size cylindrical roughness elements in a laminar, compressible, three-dimensional boundary layer on a wing profile are investigated by direct numerical simulations (DNS). Large elements are capable of immediately tripping turbulent flow by either a strong, purely convective or an absolute/global instability in the near wake. First we focus on an understanding of the steady near-field past a finite-size roughness element in the swept-wing flow, comparing it to a respective case in unswept flow. Then, the mechanisms leading to immediate turbulence tripping are elaborated by gradually increasing the roughness height and varying the disturbance background level. The quasi-critical roughness Reynolds number above which turbulence sets in rapidly is found to be 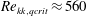 $Re_{kk,qcrit}\approx 560$ and global instability is found only for values well above 600 using nonlinear DNS; therefore the values do not differ significantly from two-dimensional boundary layers if the full velocity vector at the roughness height is taken to build
$Re_{kk,qcrit}\approx 560$ and global instability is found only for values well above 600 using nonlinear DNS; therefore the values do not differ significantly from two-dimensional boundary layers if the full velocity vector at the roughness height is taken to build 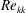 $Re_{kk}$. A detailed simulation study of elements in the critical range indicates a changeover from a purely convective to a global instability near the critical height. Finally, we perform a three-dimensional global stability analysis of the flow field to gain insight into the early stages of the temporal disturbance growth in the quasi-critical and over-critical cases, starting from a steady state enforced by damping of unsteady disturbances.
$Re_{kk}$. A detailed simulation study of elements in the critical range indicates a changeover from a purely convective to a global instability near the critical height. Finally, we perform a three-dimensional global stability analysis of the flow field to gain insight into the early stages of the temporal disturbance growth in the quasi-critical and over-critical cases, starting from a steady state enforced by damping of unsteady disturbances.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
Kurz et al. supplementary movie
“Mechanisms of flow tripping by discrete roughness elements in a swept-wing boundary layer”. Movie to §6, 6.1.-6.3, figures 11-17, of the paper. Vortex visualization using λ2, the colour indicates the sign of the streamwise vorticity: red is for rotation sense in clockwise direction when looking downstream. Quasi-critical roughness case, Rekk=564. Phase 1: start from enforced steady state w/o controlled unsteady forcing; phase 2: controlled pulsing switched on; phase 3: controlled pulsing switched off.
Kurz et al. supplementary movie
“Mechanisms of flow tripping by discrete roughness elements in a swept-wing boundary layer”. Movie to §6, 6.4, figures 19-20, of the paper. Vortex visualization using λ2, the colour indicates the sign of the streamwise vorticity: red is for rotation sense in clockwise direction when looking downstream. Over-critical roughness case, Rekk=881. Start from enforced steady state w/o controlled unsteady forcing; convective instability is seen first, followed by appearance of global instability.
- 47
- Cited by



