Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eshbal, L.
Kovalev, D.
Rinsky, V.
Greenblatt, D.
and
van Hout, R.
2019.
Tomo-PIV measurements in the wake of a tethered sphere undergoing VIV.
Journal of Fluids and Structures,
Vol. 89,
Issue. ,
p.
132.
Sansica, A.
Ohmichi, Y.
Robinet, J.-Ch.
and
Hashimoto, A.
2020.
Laminar supersonic sphere wake unstable bifurcations.
Physics of Fluids,
Vol. 32,
Issue. 12,
David, Tom
Eshbal, Lior
Rinsky, Vladislav
and
van Hout, René
2020.
Flow measurements in the near wake of a smooth sphere and one mimicking a pine cone.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Khan, Majid Hassan
Khan, Hamid Hassan
Sharma, Atul
and
Agrawal, Amit
2020.
Laminar Vortex Shedding in the Wake of a Cube.
Journal of Fluids Engineering,
Vol. 142,
Issue. 11,
Long, Yun
Long, Xinping
and
Ji, Bin
2020.
LES investigation of cavitating flows around a sphere with special emphasis on the cavitation–vortex interactions.
Acta Mechanica Sinica,
Vol. 36,
Issue. 6,
p.
1238.
Yao, Weiguang
Zhang, Hui
Jiang, Daiwen
Gui, Mingyue
Zhao, Zijie
and
Chen, Zhihua
2021.
Mode transformations of vortex shedding behind a sphere with the effect of Lorentz force.
Physics of Fluids,
Vol. 33,
Issue. 12,
Muyshondt, Robert
Nguyen, Thien
Hassan, Y. A.
and
Anand, N. K.
2021.
Experimental Measurements of the Wake of a Sphere at Subcritical Reynolds Numbers.
Journal of Fluids Engineering,
Vol. 143,
Issue. 6,
Cao, Liu-shuai
Huang, Feng-lai
Liu, Cheng
and
Wan, De-cheng
2021.
Vortical structures and wakes of a sphere in homogeneous and density stratified fluid.
Journal of Hydrodynamics,
Vol. 33,
Issue. 2,
p.
207.
Shang, Wenqiang
Zhao, Hui
Li, Dong
Luo, Kun
and
Fan, Jianren
2021.
Direct numerical simulation of the flow around a sphere immersed in a flat-plate turbulent boundary layer.
Physics of Fluids,
Vol. 33,
Issue. 11,
Li, Xing
Zhang, Haibin
and
Bai, Bofeng
2021.
Dye visualization of the wake of a near-wall particle in response to a periodic oscillation.
Measurement: Sensors,
Vol. 13,
Issue. ,
p.
100032.
Rooney, David M.
Mortimer, Patrick
Tricouros, Frank A.
and
Vaccaro, John C.
2022.
Wake Flow Measurements Behind Rotating Smooth Spheres and Baseballs Near Critical Reynolds Numbers.
Journal of Fluids Engineering,
Vol. 144,
Issue. 3,
Ma, Likun
Kashanj, Sina
Xu, Shuliang
Zhou, Jibin
Nobes, David S.
and
Ye, Mao
2022.
Flow Reconstruction and Prediction Based on Small Particle Image Velocimetry Experimental Datasets with Convolutional Neural Networks.
Industrial & Engineering Chemistry Research,
Vol. 61,
Issue. 24,
p.
8504.
Kovalev, D.
Eshbal, L.
and
van Hout, R.
2022.
Three-dimensional flow field measurements in the wake of a tethered sphere crossing the onset of vortex induced vibrations.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Kato, Hayato
Takamure, Kotaro
and
Uchiyama, Tomomi
2022.
Characteristics of vortex shedding in the wake of a sphere with a uniaxial through-hole.
AIP Advances,
Vol. 12,
Issue. 10,
Young, D. L.
Li, J.-S.
Capart, H.
and
Chu, C.-R.
2022.
Velocity measurements of vortex structures induced by sphere/wall interaction.
Experiments in Fluids,
Vol. 63,
Issue. 11,
Hou, Chang
Deng, Nan
and
Noack, Bernd R.
2022.
Trajectory-optimized cluster-based network model for the sphere wake.
Physics of Fluids,
Vol. 34,
Issue. 8,
Li, Dong
Luo, Kun
Zhao, Hui
Shang, Wenqiang
and
Fan, Jianren
2022.
Interaction between a stationary sphere and turbulent flow in a boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 8,
Han, Zhenze
Sun, Kangfu
Chen, Wenyi
and
Sun, Jiao
2023.
Experimental investigation on the wake structure of teardrop-shape slender body.
Ocean Engineering,
Vol. 280,
Issue. ,
p.
114789.
Gold, Thomas
Reiterer, Kevin
Worf, Dominik
Khosronejad, Ali
Habersack, Helmut
and
Sindelar, Christine
2023.
Lagrangian particle tracking velocimetry investigation of vortex shedding topology for oscillating heavy spherical pendulums underwater.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
Hayden, Andrew P.
Hefner, Cole
Gillespie, John
Untaroiu, Alexandrina
and
Lowe, Todd
2023.
A Computational and Experimental Analysis of Vortex Shedding from Complex Turning Vanes.
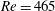 $Re=465$
$Re=465$