Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-20T06:31:31.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean field control of droplet dynamics with high-order finite-element computations

Published online by Cambridge University Press:  20 November 2024

Guosheng Fu ,
Hangjie Ji Open the ORCID record for Hangjie Ji [Opens in a new window] ,
Will Pazner  and
Wuchen Li Open the ORCID record for Wuchen Li [Opens in a new window]
Guosheng Fu
Affiliation:
Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, IN 46556, USA
Hangjie Ji
Affiliation:
Department of Mathematics, North Carolina State University, NC 27695, USA
Will Pazner
Affiliation:
Fariborz Maseeh Department of Mathematics and Statistics, Portland State University, Portland, OR 97207, USA
Wuchen Li*
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, SC 29208, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

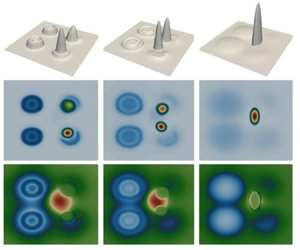
Liquid droplet dynamics are widely used in biological and engineering applications, which contain complex interfacial instabilities and pattern formation such as droplet merging, splitting and transport. This paper studies a class of mean field control formulations for these droplet dynamics, which can be used to control and manipulate droplets in applications. We first formulate the droplet dynamics as gradient flows of free energies in modified optimal transport metrics with nonlinear mobilities. We then design an optimal control problem for these gradient flows. As an example, a lubrication equation for a thin volatile liquid film laden with an active suspension is developed, with control achieved through its activity field. Lastly, we apply the primal–dual hybrid gradient algorithm with high-order finite-element methods to simulate the proposed mean field control problems. Numerical examples, including droplet formation, bead-up/spreading, transport, and merging/splitting on a two-dimensional spatial domain, demonstrate the effectiveness of the proposed mean field control mechanism.

JFM classification

Flow Control: Control theory Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 999 , 25 November 2024 , A76
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aditi Simha, R. & Ramaswamy, S. 2002 Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89 (5), 058101.CrossRefGoogle ScholarPubMed
Adkins, R., Kolvin, I., You, Z., Witthaus, S., Marchetti, M.C. & Dogic, Z. 2022 Dynamics of active liquid interfaces. Science 377 (6607), 768–772.CrossRefGoogle ScholarPubMed
Ajaev, V.S. 2005 a Evolution of dry patches in evaporating liquid films. Phys. Rev. E 72 (3), 031605.CrossRefGoogle ScholarPubMed
Ajaev, V.S. 2005 b Spreading of thin volatile liquid droplets on uniformly heated surfaces. J. Fluid Mech. 528, 279–296.CrossRefGoogle Scholar
Ajaev, V.S. & Homsy, G.M. 2001 Steady vapor bubbles in rectangular microchannels. J. Colloid Interface Sci. 240 (1), 259–271.CrossRefGoogle ScholarPubMed
Al Jamal, R. & Morris, K. 2018 Linearized stability of partial differential equations with application to stabilization of the Kuramoto–Sivashinsky equation. SIAM J. Control Optim. 56 (1), 120–147.CrossRefGoogle Scholar
Anderson, R., Andrej, J., Barker, A., et al. 2021 MFEM: a modular finite element methods library. Comput. Maths Appl. 81, 42–74.CrossRefGoogle Scholar
Armaou, A. & Christofides, P.D. 2000 Feedback control of the Kuramoto–Sivashinsky equation. Physica D 137 (1–2), 49–61.CrossRefGoogle Scholar
Benamou, J.-D. & Brenier, Y. 2000 A computational fluid mechanics solution to the Monge–Kantorovich mass transfer problem. Numer. Math. 84 (3), 375–393.CrossRefGoogle Scholar
Bertozzi, A.L., Grün, G. & Witelski, T.P. 2001 Dewetting films: bifurcations and concentrations. Nonlinearity 14 (6), 1569.CrossRefGoogle Scholar
Biswal, S., Ji, H., Elamvazhuthi, K. & Bertozzi, A.L. 2024 Optimal boundary control of a model thin-film fiber coating model. Physica D 457, 133942.CrossRefGoogle Scholar
Boffi, D., Brezzi, F. & Fortin, M. 2013 Mixed Finite Element Methods and Applications. Springer Series in Computational Mathematics, vol. 44. Springer.CrossRefGoogle Scholar
Burelbach, J.P., Bankoff, S.G. & Davis, S.H. 1988 Nonlinear stability of evaporating/condensing liquid films. J. Fluid Mech. 195, 463–494.CrossRefGoogle Scholar
Carrillo, J.A., Craig, K., Wang, L. & Wei, C. 2022 Primal dual methods for Wasserstein gradient flows. Found. Comput. Maths 22 (2), 389–443.CrossRefGoogle Scholar
Carrillo, J.A., Wang, L. & Wei, C. 2023 Structure preserving primal dual methods for gradient flows with nonlinear mobility transport distances. SIAM J. Numer. Anal. 62 (1), 376–399.Google Scholar
Chambolle, A. & Pock, T. 2011 A first-order primal–dual algorithm for convex problems with applications to imaging. J. Math. Imag. Vis. 40 (1), 120–145.CrossRefGoogle Scholar
Chandel, G.R., Sivasankar, V.S. & Das, S. 2024 Evaporation of active drops: puncturing drops and particle deposits of ring galaxy patterns. Phys. Rev. Fluids 9 (3), 033603.CrossRefGoogle Scholar
Christofides, P.D. & Armaou, A. 2000 Global stabilization of the Kuramoto–Sivashinsky equation via distributed output feedback control. Syst. Control Lett. 39 (4), 283–294.CrossRefGoogle Scholar
Chu, W., Ji, H., Wang, Q., Kim, C.-J.C.J., Bertozzi, A.L., et al. 2023 Electrohydrodynamics modeling of droplet actuation on a solid surface by surfactant-mediated electrodewetting. Phys. Rev. Fluids 8 (7), 073701.CrossRefGoogle Scholar
Cimpeanu, R., Gomes, S.N. & Papageorgiou, D.T. 2021 Active control of liquid film flows: beyond reduced-order models. Nonlinear Dyn. 104 (1), 267–287.CrossRefGoogle Scholar
Coron, J.-M. & Lü, Q. 2015 Fredholm transform and local rapid stabilization for a Kuramoto–Sivashinsky equation. J. Differ. Equ. 259 (8), 3683–3729.CrossRefGoogle Scholar
Dukler, Y., Ji, H., Falcon, C. & Bertozzi, A.L. 2020 Theory for undercompressive shocks in tears of wine. Phys. Rev. Fluids 5 (3), 034002.CrossRefGoogle Scholar
Eaker, C.B. & Dickey, M.D. 2016 Liquid metal actuation by electrical control of interfacial tension. Appl. Phys. Rev. 3 (3), 031103.CrossRefGoogle Scholar
Fu, G., Ji, H., Pazner, W. & Li, W. 2024 a Mean-field control for droplet dynamics. GitHub repository: https://github.com/gridfunction/DROPLET_MFC.Google Scholar
Fu, G., Osher, S. & Li, W. 2023 High order spatial discretization for variational time implicit schemes: Wasserstein gradient flows and reaction–diffusion systems. J. Comput. Phys. 491, 112375.CrossRefGoogle Scholar
Fu, G., Osher, S., Pazner, W. & Li, W. 2024 b Generalized optimal transport and mean field control problems for reaction–diffusion systems with high-order finite element computation. J. Comput. Phys. 508, 112994.CrossRefGoogle Scholar
Gao, Y. & Qi, D. 2024 Mean field games for controlling coherent structures in nonlinear fluid systems. arXiv:2401.10356.Google Scholar
Glasner, K.B. & Witelski, T.P. 2003 Coarsening dynamics of dewetting films. Phys. Rev. E 67 (1), 016302.CrossRefGoogle ScholarPubMed
Greer, J.B., Bertozzi, A.L. & Sapiro, G. 2006 Fourth order partial differential equations on general geometries. J. Comput. Phys. 216 (1), 216–246.CrossRefGoogle Scholar
Jacobs, M., Léger, F., Li, W. & Osher, S. 2019 Solving large-scale optimization problems with a convergence rate independent of grid size. SIAM J. Numer. Anal. 57 (3), 1100–1123.CrossRefGoogle Scholar
Ji, H., Falcon, C., Sadeghpour, A., Zeng, Z., Ju, Y.S. & Bertozzi, A.L. 2019 Dynamics of thin liquid films on vertical cylindrical fibres. J. Fluid Mech. 865, 303–327.CrossRefGoogle Scholar
Ji, H., Falcon, C., Sedighi, E., Sadeghpour, A., Ju, Y.S. & Bertozzi, A.L. 2021 Thermally-driven coalescence in thin liquid film flowing down a fibre. J. Fluid Mech. 916, A19.CrossRefGoogle Scholar
Ji, H. & Witelski, T.P. 2018 Instability and dynamics of volatile thin films. Phys. Rev. Fluids 3 (2), 024001.CrossRefGoogle Scholar
Ji, H. & Witelski, T.P. 2024 Coarsening of thin films with weak condensation. SIAM J. Appl. Maths 84 (2), 362–386.CrossRefGoogle Scholar
Jiang, Y., Feng, L., O'Donnell, A., Machado, C., Choi, W., Patankar, N.A. & Park, K.-C. 2022 Coalescence-induced propulsion of droplets on a superhydrophilic wire. Appl. Phys. Lett. 121 (23), 231602.CrossRefGoogle Scholar
Joanny, J.-F. & Ramaswamy, S. 2012 A drop of active matter. J. Fluid Mech. 705, 46–57.CrossRefGoogle Scholar
Jordan, R., Kinderlehrer, D. & Otto, F. 1998 The variational formulation of the Fokker–Planck equation. SIAM J. Math. Anal. 29 (1), 1–17.CrossRefGoogle Scholar
Katz, R. & Fridman, E. 2020 Finite-dimensional control of the Kuramoto–Sivashinsky equation under point measurement and actuation. In 2020 59th IEEE Conference on Decision and Control (CDC) Jeju, South Korea, pp. 4423–4428. IEEE.CrossRefGoogle Scholar
Khoshmanesh, K., Tang, S.-Y., Zhu, J.Y., Schaefer, S., Mitchell, A., Kalantar-Zadeh, K. & Dickey, M.D. 2017 Liquid metal enabled microfluidics. Lab on a Chip 17 (6), 974–993.CrossRefGoogle ScholarPubMed
Kim, C.-J.C.J. 2001 Micropumping by electrowetting. In ASME International Mechanical Engineering Congress and Exposition, vol. 35593, pp. 55–62. American Society of Mechanical Engineers.Google Scholar
Klein, M. & Prohl, A. 2016 Optimal control for the thin film equation: convergence of a multi-parameter approach to track state constraints avoiding degeneracies. Comput. Meth. Appl. Maths 16 (4), 685–702.CrossRefGoogle Scholar
Lee, C.H. & Tran, H.T. 2005 Reduced-order-based feedback control of the Kuramoto–Sivashinsky equation. J. Comput. Appl. Maths 173 (1), 1–19.CrossRefGoogle Scholar
Li, J., Ha, N.S., Liu, T.L., van Dam, R.M. & Kim, C.-J.C.J. 2019 Ionic-surfactant-mediated electro-dewetting for digital microfluidics. Nature 572 (7770), 507–510.CrossRefGoogle ScholarPubMed
Li, W., Lee, W. & Osher, S. 2022 a Computational mean-field information dynamics associated with reaction–diffusion equations. J. Comput. Phys. 466, Paper No. 111409, 30.CrossRefGoogle Scholar
Li, W., Liu, S. & Osher, S. 2022 b Controlling conservation laws. II. Compressible Navier–Stokes equations. J. Comput. Phys. 463, 111264.CrossRefGoogle Scholar
Li, W., Liu, S. & Osher, S. 2023 Controlling conservation laws. I. Entropy-entropy flux. J. Comput. Phys. 480.CrossRefGoogle Scholar
Li, W., Lu, J. & Wang, L. 2020 Fisher information regularization schemes for Wasserstein gradient flows. J. Comput. Phys. 416, 109449, 24.CrossRefGoogle Scholar
Liu, W.-J. & Krstić, M. 2001 Stability enhancement by boundary control in the Kuramoto–Sivashinsky equation. Nonlinear Anal. 43 (4), 485–507.CrossRefGoogle Scholar
Loisy, A., Eggers, J. & Liverpool, T.B. 2019 Tractionless self-propulsion of active drops. Phys. Rev. Lett. 123 (24), 248006.CrossRefGoogle ScholarPubMed
Maass, C.C., Krüger, C., Herminghaus, S. & Bahr, C. 2016 Swimming droplets. Annu. Rev. Condens. Matt. Phys. 7, 171–193.CrossRefGoogle Scholar
Maghenem, M., Prieur, C. & Witrant, E. 2022 Boundary control of the Kuramoto–Sivashinsky equation under intermittent data availability. In 2022 American Control Conference (ACC), Atlanta, GA, pp. 2227–2232.Google Scholar
Marchetti, M.C., Joanny, J.-F., Ramaswamy, S., Liverpool, T.B., Prost, J., Rao, M. & Simha, R.A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143.CrossRefGoogle Scholar
Michelin, S. 2023 Self-propulsion of chemically active droplets. Annu. Rev. Fluid Mech. 55, 77–101.CrossRefGoogle Scholar
Mielke, A. 2011 A gradient structure for reaction–diffusion systems and for energy-drift-diffusion systems. Nonlinearity 24 (4), 1329–1346.CrossRefGoogle Scholar
Nan, L., Mao, T. & Shum, H.C. 2023 Self-synchronization of reinjected droplets for high-efficiency droplet pairing and merging. Microsyst. Nanoengng 9 (1), 24.CrossRefGoogle ScholarPubMed
Nelson, W.C. & Kim, C.-J.C.J. 2012 Droplet actuation by electrowetting-on-dielectric (EWOD): a review. J. Adhes. Sci. Technol. 26 (12–17), 1747–1771.CrossRefGoogle Scholar
Oron, A. & Bankoff, S.G. 2001 Dynamics of a condensing liquid film under conjoining/disjoining pressures. Phys. Fluids 13 (5), 1107–1117.CrossRefGoogle Scholar
Oron, A., Davis, S.H. & Bankoff, S.G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931.CrossRefGoogle Scholar
Pazner, W., Kolev, T. & Dohrmann, C.R. 2023 Low-order preconditioning for the high-order finite element de Rham complex. SIAM J. Sci. Comput. 45 (2), A675–A702.CrossRefGoogle Scholar
Ruyer-Quil, C., Treveleyan, P., Giorgiutti-Dauphiné, F., Duprat, C. & Kalliadasis, S. 2008 Modelling film flows down a fibre. J. Fluid Mech. 603, 431–462.CrossRefGoogle Scholar
Sadeghpour, A., Oroumiyeh, F., Zhu, Y., Ko, D.D., Ji, H., Bertozzi, A.L. & Ju, Y.S. 2021 Experimental study of a string-based counterflow wet electrostatic precipitator for collection of fine and ultrafine particles. J. Air Waste Manage. Assoc. 71 (7), 851–865.CrossRefGoogle ScholarPubMed
Sadeghpour, A., Zeng, Z., Ji, H., Dehdari Ebrahimi, N., Bertozzi, A.L. & Ju, Y.S. 2019 Water vapor capturing using an array of traveling liquid beads for desalination and water treatment. Sci. Adv. 5 (4), eaav7662.CrossRefGoogle ScholarPubMed
Samoilova, A.E. & Nepomnyashchy, A. 2019 Feedback control of Marangoni convection in a thin film heated from below. J. Fluid Mech. 876, 573–590.CrossRefGoogle Scholar
Schöberl, J. 2014 C++11 implementation of finite elements in NGSolve. ASC Report 30/2014, Institute for Analysis and Scientific Computing, Vienna University of Technology.Google Scholar
Shankar, S., Raju, V. & Mahadevan, L. 2022 Optimal transport and control of active drops. Proc. Natl Acad. Sci. USA 119 (35), e2121985119.CrossRefGoogle ScholarPubMed
Thiele, U., Archer, A.J. & Pismen, L.M. 2016 Gradient dynamics models for liquid films with soluble surfactant. Phys. Rev. Fluids 1 (8), 083903.CrossRefGoogle Scholar
Tomlin, R.J. & Gomes, S.N. 2019 Point-actuated feedback control of multidimensional interfaces. IMA J. Appl. Maths 84 (6), 1112–1142.CrossRefGoogle Scholar
Tomlin, R.J., Gomes, S.N., Pavliotis, G.A. & Papageorgiou, D.T. 2019 Optimal control of thin liquid films and transverse mode effects. SIAM J. Appl. Dyn. Syst. 18 (1), 117–149.CrossRefGoogle Scholar
Trinschek, S., Stegemerten, F., John, K. & Thiele, U. 2020 Thin-film modeling of resting and moving active droplets. Phys. Rev. E 101 (6), 062802.CrossRefGoogle ScholarPubMed
Villani, C. 2008 Optimal Transport: Old and New, vol. 338. Springer Science & Business Media.Google Scholar
Whitfield, C.A. & Hawkins, R.J. 2016 Instabilities, motion and deformation of active fluid droplets. New J. Phys. 18 (12), 123016.CrossRefGoogle Scholar
Witelski, T.P. & Bowen, M. 2003 ADI schemes for higher-order nonlinear diffusion equations. Appl. Numer. Maths 45 (2–3), 331–351.CrossRefGoogle Scholar
Wray, A.W., Cimpeanu, R. & Gomes, S.N. 2022 Electrostatic control of the Navier–Stokes equations for thin films. Phys. Rev. Fluids 7 (12), L122001.CrossRefGoogle Scholar
Wray, A.W., Papageorgiou, D.T., Craster, R.V., Sefiane, K. & Matar, O.K. 2015 Electrostatic suppression of the “coffee-stain effect”. Procedia IUTAM 15, 172–177, iUTAM Symposium on Multiphase Flows with Phase Change: Challenges and Opportunities.CrossRefGoogle Scholar
Supplementary material: File

Fu et al. supplementary movie

Controlled droplet splitting dynamics
Download Fu et al. supplementary movie(File)
File 410.5 KB