Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T01:36:36.829Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean dynamics and transition to turbulence in oscillatory channel flow

Published online by Cambridge University Press:  18 October 2019

Alireza Ebadi Open the ORCID record for Alireza Ebadi [Opens in a new window] ,
Christopher M. White Open the ORCID record for Christopher M. White [Opens in a new window] ,
Ian Pond  and
Yves Dubief
Alireza Ebadi
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Christopher M. White*
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Ian Pond
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Yves Dubief
Affiliation:
School of Engineering, University of Vermont, Burlington, VT 05405, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The mean dynamics in oscillatory channel flow is examined to investigate the dynamical mechanisms underlying the transition to turbulence in oscillatory wall-bounded flow. The analyses employ direct numerical simulation data acquired at three Stokes Reynolds numbers: 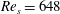$Re_{s}=648$, 801 and 1009, where the lower 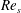$Re_{s}$ flow is transitional over the entire cycle and the two higher 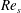$Re_{s}$ flows exhibit flow characteristics similar to steady turbulent wall-bounded flow during part of the cycle. The flow evolution over a half-period of oscillation for all three 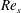$Re_{s}$ is as follows: near-wall streamwise velocity streaks develop during the early accelerating portion of the cycle; then at some later point in the cycle that depends on 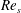$Re_{s}$, the near-wall streaks breakdown (demarking the onset of the nonlinear development stage), and the near-wall Reynolds stress grows explosively; the Reynolds stress remains elevated for part of the cycle before diminishing (yet remaining finite) during the late decelerating portion of the cycle. This process is then repeated indefinitely. The present findings demonstrate that transition to turbulence occurs when the nonlinear development stage begins during the accelerating portion of the cycle. This crucially leads to the diminishing importance of the centreline momentum source, the emergence of a locally accelerating/decelerating internal layer centred about the edge of the Stokes layer and the wall-normal rearrangement of the mean forces prior to the start of the decelerating portion of the cycle. The rearrangement of mean forces culminates in a four layer structure in the mean balance of forces. This is significant on a number of accounts since empirical and theoretical evidence suggests that the formation of a four layer structure is an important characteristic of a self-similar hierarchal structure that underlies logarithmic dependence of the mean velocity profile in steady turbulent wall-bounded flows (Klewicki et al., J. Fluid Mech., vol. 638, 2009, pp. 73–93). When the nonlinear development stage begins during the decelerating portion of the cycle (i.e. at 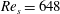$Re_{s}=648$), a four layer structure is not observed in the mean balance of forces and the flow remains weakly transitional over the entire cycle.

JFM classification

Instability: Transition to turbulence Turbulent Flows: Turbulent boundary layers Boundary Layers: Boundary layer structure
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 864 - 889
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhavan, R., Kamm, R. D. & Shapiro, A. H. 1991a An investigation of transition to turbulence in bounded oscillatory Stokes flows. Part 1. Experiments. J. Fluid Mech. 225, 395–422.10.1017/S0022112091002100Google Scholar
Akhavan, R., Kamm, R. D. & Shapiro, A. H. 1991b An investigation of transition to turbulence in bounded oscillatory Stokes flows. Part 2. Numerical simulations. J. Fluid Mech. 225, 423–444.10.1017/S0022112091002112Google Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.Google Scholar
Di Liberto, M. & Ciofalo, M. 2011 Unsteady turbulence in plane channel flow. Comput. Fluids 49 (1), 258–275.10.1016/j.compfluid.2011.06.007Google Scholar
Dubief, Y., Terrapon, V. E., White, C. M., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74 (4), 311–329.10.1007/s10494-005-9002-6Google Scholar
Eckmann, D. M. & Grotberg, J. B. 1991 Experiments on transition to turbulence in oscillatory pipe flow. J. Fluid Mech. 222, 329–350.10.1017/S002211209100112XGoogle Scholar
Elsnab, J., Klewicki, J., Maynes, D. & Ameel, T. 2011 Mean dynamics of transitional channel flow. J. Fluid Mech. 678, 451–481.Google Scholar
Frohnapfel, B., Lammers, P., Jovanović, J. & Durst, F. 2007 Interpretation of the mechanism associated with turbulent drag reduction in terms of anisotropy invariants. J. Fluid Mech. 577, 457–466.10.1017/S0022112007005083Google Scholar
Hino, M., Sawamoto, M. & Takasu, S. 1976 Experiments on transition to turbulence in an oscillatory pipe flow. J. Fluid Mech. 75 (2), 193–207.10.1017/S0022112076000177Google Scholar
Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.10.1017/S0022112089002302Google Scholar
Jovanović, J. & Hillerbrand, R. 2005 On peculiar property of the velocity fluctuations in wall-bounded flows. Therm. Sci. 9 (1), 3–12.10.2298/TSCI0501003JGoogle Scholar
Klewicki, J., Ebner, R. & Wu, X. 2011 Mean dynamics of transitional boundary-layer flow. J. Fluid Mech. 682, 617–651.10.1017/jfm.2011.253Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Klewicki, J. & Oberlack, M. 2015 Finite Reynolds number properties of a turbulent channel flow similarity solution. Phys. Fluids 27, 095110.Google Scholar
Kuroda, A. 1990 A direct numerical simulation of the fully developed turbulent channel flow. Numer. Meth Fluid Dyn. 2, 1012–1017.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, N31.10.1080/14685240802376389Google Scholar
Lumley, J. L. & Newman, G. R. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82 (1), 161–178.Google Scholar
Miller, J. A. & Fejer, A. A. 1964 Transition phenomena in oscillating boundary-layer flows. J. Fluid Mech. 18 (03), 438–448.10.1017/S0022112064000325Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.10.1063/1.869966Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of the von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.Google Scholar
Ozdemir, C. E., Hsu, T.-J. & Balachandar, S. 2014 Direct numerical simulations of transition and turbulence in smooth-walled stokes boundary layer. Phys. Fluids 26 (4), 045108.Google Scholar
Perlman, E., Burns, R., Li, Y. & Meneveau, C. 2007 Data exploration of turbulence simulations using a database cluster. In Proceedings of the 2007 ACM/IEEE Conference on Supercomput., p. 23. ACM.Google Scholar
Schmirler, M., Matěcha, J., Netřebská, H., Ježek, J. & Adamec, J. 2014 The influence of flow parameters on the transition to turbulence in pulsatile flow. In EPJ Web Conf., vol. 67, p. 02107. EDP Sciences.Google Scholar
Scotti, A. & Piomelli, U. 2001 Numerical simulation of pulsating turbulent channel flow. Phys. Fluids 13 (5), 1367–1384.10.1063/1.1359766Google Scholar
Sergeev, S. I. 1966 Fluid oscillations in pipes at moderate Reynolds numbers. Fluid Dyn. 1 (1), 121–122.Google Scholar
Simonsen, A. J. & Krogstad, P.-Å. 2005 Turbulent stress invariant analysis: clarification of existing terminology. Phys. Fluids 17 (8), 088103.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.10.1146/annurev-fluid-122109-160753Google Scholar
Spalart, P. R. & Baldwin, B. S. 1989 Direct simulation of a turbulent oscillating boundary layer. In Turbulent Shear Flows 6, pp. 417–440. Springer.10.1007/978-3-642-73948-4_32Google Scholar
Wei, T., Fife, P., Klewicki, J. & Mcmurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30R long turbulent pipe flow at R + = 685: large- and very large-scale motions. J. Fluid Mech. 698, 235–281.10.1017/jfm.2012.81Google Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22 (8), 085105.10.1063/1.3475816Google Scholar