Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-19T12:29:35.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Mapping spheroid rotation modes in turbulent channel flow: effects of shear, turbulence and particle inertia

Published online by Cambridge University Press:  31 July 2019

Lihao Zhao Open the ORCID record for Lihao Zhao [Opens in a new window] ,
Niranjan R. Challabotla ,
Helge I. Andersson  and
Evan A. Variano
Lihao Zhao*
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, 100084 Beijing, China Department of Energy and Process Engineering, Norwegian University of Science and Technology, 7491 Trondheim, Norway
Niranjan R. Challabotla
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, 7491 Trondheim, Norway
Helge I. Andersson
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, 7491 Trondheim, Norway
Evan A. Variano
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The rotational behaviour of non-spherical particles in turbulent channel flow is studied by Lagrangian tracking of spheroidal point particles in a directly simulated flow. The focus is on the complex rotation modes of the spheroidal particles, in which the back reaction on the flow field is ignored. This study is a sequel to the letter by Zhao et al. (Phys. Rev. Lett., vol. 115, 2015, 244501), in which only selected results in the near-wall buffer region and the almost-isotropic channel centre were presented. Now, particle dynamics all across the channel is explored to provide a complete picture of the orientational and rotational behaviour with consideration of the effects of particle aspect ratio ranging from 0.1 to 10 and particle Stokes number from 0 (inertialess) to 30. The rotational dynamics in the innermost part of the logarithmic wall layer is particularly complex and affected not only by modest mean shear, but also by particle inertia and turbulent vorticity. While inertial disks exhibit modest preferential orientation in either the wall-normal or cross-stream direction, inertial rods show neither preferential tumbling nor spinning. Examination of the co-variances between particle orientation, particle rotation and fluid rotation vectors explains the qualitatively different ‘wall mode’ rotation and ‘centre mode’ rotation. Inertialess spheroids transition between the two modes within a narrow zone (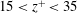$15<z^{+}<35$) in the buffer region. If the spheroids have inertia, the transition zone between the two modes shifts to the inner part of the logarithmic layer, i.e. 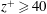$z^{+}\geqslant 40$. We ascribe the transition of inertialess spheroids from the ‘wall mode’ to the ‘centre mode’ rotation to the changeover between the time scales associated with mean shear and small-scale turbulence. Inertial spheroids, however, transition between the two rotational modes when the Kolmogorov time scale becomes comparable to the time scale for particle rotation, i.e. the effective Stokes number is of order unity. The aforementioned findings reveal, in addition to the effects of particle shape and alignment, the importance of the characteristic local time scale of fluid flow for the rotation of both tracer and inertial spheroids in turbulent channel flows.

JFM classification

Complex Fluids: Suspensions Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 19 - 54
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anand, C., Shotorban, B. & Mahalingam, S. 2018 Dispersion and deposition of firebrands in a turbulent boundary layer. Intl J. Multiphase Flow 109, 98–113.Google Scholar
Andersson, H. I. & Jiang, F. 2019 Forces and torques on a prolate spheroid: low-Reynolds-number and attack angle effects. Acta Mechanica 230, 431–447.Google Scholar
Andersson, H. I., Zhao, L. & Variano, E. A. 2015 On the anisotropic vorticity in turbulent channel flows. Trans. ASME J. Fluids Engng 137, 084503.Google Scholar
Antonia, R. A., Kim, J. & Browne, L. B. W. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.Google Scholar
Ardekani, M. N., Costa, P., Breugem, W. P., Picano, F. & Brandt, L. 2017a Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.Google Scholar
Ardekani, M. N., Sardina, G., Brandt, L., Karp-Boss, L., Bearon, R. N. & Variano, E. A. 2017b Sedimentation of inertia-less prolate spheroids in homogeneous isotropic turbulence with application to non-motile phytoplankton. J. Fluid Mech. 831, 655–674.Google Scholar
Balachandar, S. 2009 A scaling analysis for point-particle approaches to turbulent multiphase flows. Intl J. Multiphase Flow 35, 801–810.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Balachandar, S., Liu, K. & Lakhote, M. 2019 Self-induced velocity correction for improved drag estimation in Euler-Lagrange point-particle simulations. J. Comput. Phys. 376, 160–185.Google Scholar
Barboza, L. G. A. & Gimenez, B. C. G. 2015 Microplastics in the marine environment. Mar. Pollut. Bull. 97, 5–12.Google Scholar
Brenner, H. 1964 The Stokes resistance of an arbitrary particle – II: An extension. Chem. Engng Sci. 19, 599–629.Google Scholar
Byron, M., Einarsson, J., Gustavsson, K., Voth, G. A., Mehlig, B. & Variano, E. A. 2015 Shape-dependence of particle rotation in isotropic turbulence. Phys. Fluids 27, 035105.Google Scholar
Challabotla, N. R., Nilsen, C. & Andersson, H. I. 2015a On rotational dynamics of inertial disks in creeping shear flow. Phys. Lett. A 379, 157–162.Google Scholar
Challabotla, N. R., Zhao, L. & Andersson, H. I. 2015b Shape effects on dynamics of inertia-free spheroids in wall turbulence. Phys. Fluids 27, 061703.Google Scholar
Challabotla, N. R., Zhao, L. & Andersson, H. I. 2015c Orientation and rotation of inertial disk particles in wall turbulence. J. Fluid Mech. 766, R2.Google Scholar
Challabotla, N. R., Zhao, L. & Andersson, H. I. 2016 Orientation and rotation dynamics of triaxial ellipsoidal tracers in wall turbulence. Phys. Fluids 28, 123304.Google Scholar
Chen, J., Jin, G. & Zhang, J. 2016 Large eddy simulation of orientation and rotation of ellipsoidal particles in isotropic turbulent flows. J. Turbul. 17, 308–326.Google Scholar
Cui, Y., Ravnik, J., Hribersek, M. & Steinmann, P. 2018 A novel model for the lift force acting on a prolate spheroidal particle in an arbitrary non-uniform flow. Part I. Lift force due to the streamwise flow shear. Intl J. Multiphase Flow 104, 103–112.Google Scholar
Devenish, B. J., Bartello, P., Brenguier, J.-L., Collins, L. R., Grabowski, W. W., Ijzermans, R. H. A., Malinowski, S. P., Reeks, M. W., Vassilicos, J. C., Wang, L.-P. et al. 2012 Droplet growth in warm turbulent clouds. Q. J. R. Meteorol. Soc. 138, 1401–1429.Google Scholar
Do-Quang, M., Amberg, G., Brethouwer, G. & Johansson, A. V. 2014 Simulation of finite-size fibers in turbulent channel flows. Phys. Rev. E 89, 013006.Google Scholar
Eaton, J. K. 2009 Two-way coupled turbulence simulations of gas-particle flows using point-particle tracking. Intl J. Multiphase Flow 35, 792–800.Google Scholar
Einarsson, J., Angilella, J. R. & Mehlig, B. 2014 Orientational dynamics of weakly inertial axisymmetric particles in steady viscous flows. Phys. D 278–279, 79–85.Google Scholar
Einarsson, J., Candelier, F., Lundell, F., Angilella, J. R. & Mehlig, B. 2015 Rotation of a spheroid in a simple shear at small Reynolds number. Phys. Fluids 27, 063301.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52, 309–329.Google Scholar
Elghobashi, S. 2006 An updated classification map of particle-laden turbulent flows. In Proceedings of the IUTAM Symposium on Computational Multiphase Flow (ed. Balachandar, S. & Prosperetti, A.), pp. 3–10. Springer.Google Scholar
Eshghinejadfard, A., Hosseini, S. A. & Thévenin, D. 2017 Fully-resolved prolate spheroids in turbulent channel flows: a lattice Boltzmann study. AIP Adv. 7, 095007.Google Scholar
Eshghinejadfard, A., Zhao, L. & Thévenin, D. 2018 Lattice-Boltzmann simulation of resolved oblate spheroids in wall turbulence. J. Fluid Mech. 849, 510–540.Google Scholar
Fan, F. G. & Ahmadi, G. 1995 Dispersion of ellipsoidal particles in an isotropic pseudo-turbulent flow field. Trans. ASME J. Fluids Engng 117, 154–161.Google Scholar
Frölich, K., Schneiders, L., Meinke, M. & Schröder, W.2018 Assessment of non-spherical pointparticle models in LES using direct particle-fluid simulations. In AIAA Fluid Dynamics Conference, Atlanta, Georgia. AIAA 2018-3714.Google Scholar
Gallily, I. & Cohen, A.-H. 1979 On the orderly nature of the motion of nonspherical aerosol particles. II. Inertial collision between a spherical large droplet and an axially symmetrical elongated particle. J. Colloid Interface Sci. 68, 338–356.Google Scholar
Galloway, T. S., Cole, M. & Lewis, C. 2017 Interactions of microplastic debris throughout the marine ecosystem. Nat. Ecol. Evol. 1, 0116.Google Scholar
Gillissen, J. J. J., Boersma, B. J., Mortensen, P. H. & Andersson, H. I. 2007 On the performance of the moment approximation for the numerical computation of fibre stress in turbulent channel flow. Phys. Fluids 19, 035102.Google Scholar
Goldstein, H. 1980 Classical Mechanics, 2nd edn. Addison Wesley.Google Scholar
Hamaoui-Laguel, L., Vautard, R., Liu, L., Solmon, F., Viovy, N., Khvorosthyanov, D., Essl, F., Chuine, I., Colette, A. & Semenov, M. A. 2015 Effects of climate change and seed dispersal on airborne ragweed pollen loads in Europe. Nat. Clim. Change 5, 766–771.Google Scholar
Horwitz, J. A. K. & Mani, A. 2016 Accurate calculation of Stokes drag for point-particle tracking in two-way coupled flows. J. Comput. Phys. 318, 85–109.Google Scholar
Horwitz, J. A. K. & Mani, A. 2018 Correction scheme for point-particle models applied to a nonlinear drag law in simulations of particle-fluid interaction. Intl J. Multiphase Flow 101, 74–84.Google Scholar
Ireland, P. J. & Desjardins, O. 2017 Improving particle drag predictions in Euler-Lagrange simulations with two-way coupling. J. Comput. Phys. 338, 405–430.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kuerten, J. G. M. 2016 Point-particle DNS and LES of particle-laden turbulent flow – a state-of-the-art review. Flow Turbul. Combust. 97, 689–713.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor lenght-scale size. J. Fluid Mech. 650, 5–55.Google Scholar
Lundell, F. & Carlsson, A. 2010 Heavy ellipsoids in creeping shear flow: transitions of the particle rotation rate and orbit shape. Phys. Rev. E 81, 016323.Google Scholar
Marchioli, C. 2017 Physics and modelling of particle deposition and resuspension in wall-bounded turbulence. In Particles in Wall-bounded Turbulent Flows: Deposition, Re-suspension and Agglomeration (ed. Minier, J.-P. & Pozorski, J.), pp. 151–208. CISM International Centre for Mechanical Sciences.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Marchioli, C. & Soldati, A. 2013 Rotation statistics of fibers in wall shear turbulence. Acta Mech. 224, 2311–2329.Google Scholar
Marchioli, C., Fantoni, M. & Soldati, A. 2010 Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Phys. Fluids 22, 033301.Google Scholar
Marchioli, C., Zhao, L. & Andersson, H. I. 2016 On the relative rotational motion between rigid fibers and fluid in turbulent channel flow. Phys. Fluids 28, 013301.Google Scholar
Marcus, G. G., Parsa, S, Kramel, S., Ni, R. & Voth, G. A. 2014 Measurements of the solid-body rotation of anisotropic particles in 3D turbulence. New J. Phys. 16, 102001.Google Scholar
Maxey, M. 2017 Simulation methods for particulate flows and concentrated suspensions. Annu. Rev. Fluid Mech. 49, 171–193.Google Scholar
Mehrabadi, M., Horwitz, J. A. K., Subramaniam, S. & Mani, A. 2018 A direct comparison of particle-resolved and point-particle methods in decaying turbulence. J. Fluid Mech. 850, 336–369.Google Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2007 Particle spin in a turbulent shear flow. Phys. Fluids 19, 078109.Google Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008a Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Phys. Fluids 20, 093302.Google Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008b On the orientation of ellipsoidal particles in a turbulent shear flow. Intl J. Multiphase Flow 34, 678–683.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 643–645.Google Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109, 134501.Google Scholar
Picciotto, M., Giusti, A., Marchioli, C. & Soldati, A. 2006 Turbulence modulation by micro-particles in boundary layers. In Proceedings of the IUTAM Symposium on Computational Multiphase Flow (ed. Balachandar, S. & Prosperetti, A.), pp. 53–62. Springer.Google Scholar
Prata, A. & Tupper, A. 2009 Aviation hazards from volcanoes: the state of the science. Nat. Hazards 51, 239–244.Google Scholar
Ravnik, J., Marchioli, C., Hribersek, M. & Soldati, A. 2013 On shear lift force modelling for non-spherical particles in turbulent flows. In AIP Conference Proceedings (ed. Psihoyios, G., Simons, T. E. & Tsitouras, Ch.), vol. 1558, pp. 1107–1110. AIP Publishing.Google Scholar
Ravnik, J., Marchioli, C. & Soldati, A. 2018 Application limits of Jeffery’s theory for elongated particle torques in turbulence: a DNS assessment. Acta Mech. 229, 827–839.Google Scholar
Rosén, T., Lundell, F. & Aidun, C. K. 2014 Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow. J. Fluid Mech. 738, 563–590.Google Scholar
Rosti, M. E., Banaei, A. A., Brandt, L. & Mazzino, A. 2018 Flexible fiber reveals the two-point statistical properties of turbulence. Phys. Rev. Lett. 121, 044501.Google Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.Google Scholar
Sabban, L., Cohen, A. & van Hout, R. 2017 Temporally resolved measurements of heavy, rigid fibre translation and rotation in nearly homogeneous isotropic turbulence. J. Fluid Mech. 814, 42–68.Google Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.Google Scholar
Schneiders, L., Meinke, M. & Schröder, W. 2017a Direct particle-fluid simulation of Kolmogorov-length-scale size particles in decaying isotropic turbulence. J. Fluid Mech. 819, 188–227.Google Scholar
Schneiders, L., Meinke, M. & Schröder, W. 2017b On the accuracy of Lagrangian point-mass models for heavy non-spherical particles in isotropic turbulence. Fuel 201, 2–14.Google Scholar
Shapiro, M. & Goldenberg, M. 1993 Deposition of glass fiber particles from turbulent air flow in a pipe. J. Aero. Sci. 24, 65–87.Google Scholar
Shaw, R. A. 2003 Particle–turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.Google Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143–173.Google Scholar
Siewert, C., Kunnen, R. P. J., Meinke, M. & Schröder, W. 2014 Orientation statistics and settling velocity of ellipsoids in decaying turbulence. Atmos. Res. 142, 45–56.Google Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.Google Scholar
Tenneti, S. & Subramaniam, S. 2014 Particle-resolved direct numerical simulation for gas-solid flow model development. Annu. Rev. Fluid Mech. 46, 199–230.Google Scholar
Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20, 053305.Google Scholar
Voth, G. A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49, 249–276.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Yang, K., Zhao, L. & Andersson, H. I. 2018 Mean-shear versus orientation isotropy: effects on inertialess spheroids’ rotation mode in wall turbulence. J. Fluid Mech. 844, 796–816.Google Scholar
Yuan, W., Andersson, H. I., Zhao, L., Challabotla, N. R. & Deng, J. 2017 Dynamics of disk-like particles in turbulent vertical channel flow. Intl J. Multiphase Flow 96, 86–100.Google Scholar
Zhang, H., Ahmadi, G., Fan, F. G. & McLaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27, 971–1009.Google Scholar
Zhao, L. & Andersson, H. I. 2016 Why spheroids orient preferentially in near-wall turbulence. J. Fluid Mech. 807, 221–234.Google Scholar
Zhao, L. H., Andersson, H. I. & Gillissen, J. J. J. 2010 Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 22, 081702.Google Scholar
Zhao, L., Andersson, H. I. & Gillissen, J. J. J. 2013 Interphasial energy transfer and particle dissipation in particle-laden wall turbulence. J. Fluid Mech. 715, 32–59.Google Scholar
Zhao, L., Challabotla, N. R., Andersson, H. I. & Variano, E. A. 2015 Rotation of nonspherical particles in turbulent channel flow. Phys. Rev. Lett. 115, 244501.Google Scholar
Zhao, L., Marchioli, C. & Andersson, H. I. 2014 Slip velocity of rigid fibers in turbulent channel flow. Phys. Fluids 26, 063302.Google Scholar