Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T04:57:45.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Magnetic-field effect on thermal convection of a nematic liquid crystal at large Rayleigh numbers

Published online by Cambridge University Press:  31 January 2013

Stephan Weiss  and
Guenter Ahlers
Stephan Weiss
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
Guenter Ahlers*
Affiliation:
Department of Physics, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report on near-turbulent thermal convection of a nematic liquid crystal heated from below in a cylindrical cell with an aspect ratio (diameter/height) equal to 0.50 for Rayleigh numbers 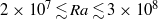$2\times 1{0}^{7} \lesssim \mathit{Ra}\lesssim 3\times 1{0}^{8} $ and a Prandtl number of about 355. The Nusselt number 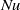$\mathit{Nu}$ as a function of 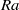$\mathit{Ra}$ did not differ significantly from that of an isotropic fluid. In a vertical magnetic field 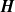$\mathbi{H}$, we found 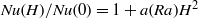$\mathit{Nu}(H)/ \mathit{Nu}(0)= 1+ a(\mathit{Ra}){H}^{2} $, with 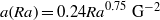$a(\mathit{Ra})= 0. 24{\mathit{Ra}}^{0. 75} ~{\mathrm{G} }^{- 2} $. We present a model that describes the 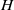$H$ dependence in terms of a change of the thermal conductivity in the thermal boundary layers due to a field-induced director alignment.

JFM classification

Convection: Buoyant boundary layers Complex Fluids: Liquid crystals
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , R7
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Current address: Department of Physics & Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA.

References

Ahlers, G. 1995 Experiments on Thermally Driven Convection, pp. 165–220, Springer.Google Scholar
Ahlers, G. 2000 Effect of sidewall conductance on heat-transport measurements for turbulent Rayleigh–Bénard convection. Phys. Rev. E 63, R015303.CrossRefGoogle ScholarPubMed
Ahlers, G. 2009 Turbulent convection. Physics 2, 74.Google Scholar
Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Cannell, D. S., Berge, L. I. & Sakurai, S. 1994 Thermal conductivity of the nematic liquid crystal 4-n-pentyl- ${4}^{\prime } $ -cyanobiphenyl. Phys. Rev. E 49, 545–553.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.Google Scholar
Ahlers, G. & Nikolaenko, A. 2010 Effect of a polymer additive on heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 034503.Google Scholar
Benzi, R., Ching, E. S. C. & Chu, V. W. S. 2011 Heat transport by laminar boundary layer flow with polymers. J. Fluid Mech. 696, 330–344.Google Scholar
Benzi, R., Ching, E. S. C. & De Angelis, E. 2010 Effect of polymer additives on heat transport in turbulent thermal convection. Phys. Rev. Lett. 104 (2), 024502.CrossRefGoogle ScholarPubMed
Boffetta, G., Mazzino, A., Musacchio, S. & Vozella, L. 2010 Polymer heat transport enhancement in thermal convection: the case of Rayleigh–Taylor turbulence. Phys. Rev. Lett. 104, 184501.Google Scholar
Bosbach, J., Weiss, S. & Ahlers, G. 2012 Plume fragmentation by bulk interactions in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 054501.Google Scholar
Brown, E. & Ahlers, G. 2007 Temperature gradients, and search for non-Boussinesq effects, in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.Google Scholar
Chandrasekhar, S. 1992 Liquid Crystals. Cambridge University Press.Google Scholar
Feng, Q., Pesch, W. & Kramer, L. 1992 Theory of Rayleigh–Bénard convection in planar nematic liquid crystals. Phys. Rev. A 45, 7242–7256.Google Scholar
Grossmann, S. & Lohse, D. 1993 Characteristic scales in Rayleigh–Bénard turbulence. Phys. Lett. A 173, 58–62.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Hidaka, Y., Huh, J., Hayashi, K., Kai, S. & Tribelsky, M. 1997 Soft-mode turbulence in electrohydrodynamic convection of a homeotropically aligned nematic layer. Phys. Rev. E 56, R6256–R6259.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
Kai, S., Hayashi, K. & Hidaka, Y. 1996 Pattern forming instability in homeotropically aligned liquid crystals. J. Phys. Chem. 100, 19007.Google Scholar
Kai, S., Zimmermann, W., Andoh, M. & Chizumi, N. 1990 Local transition to turbulence in electrohydrodynamic convection. Phys. Rev. Lett. 64, 1111–1114.Google Scholar
Khoo, I.-C. 2007 Liquid Crystals. Wiley.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Malkus, M. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Ni, R., Zhou, S.-Q. & Xia, K.-Q. 2011 An experimental investigation of turbulent thermal convection in water-based alumina nanofluid. Phys. Fluids 23, 022005.Google Scholar
Park, C., Clark, N. & Noble, R. 2005 A convective turbulente state that spatially orders upon increased drive. Phys. Fluids 17, 055101.Google Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulence convection in water. Phys. Rev. E 47, R2253–R2256.Google Scholar
Wei, P., Ni, R. & Xia, K.-Q. 2012 Enhanced and reduced heat transport in turbulent thermal convection with polymer additives. Phys. Rev. E 86, 016325.Google Scholar
Weiss, S. & Ahlers, G. 2011 Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio $\Gamma = 0. 50$ and Prandtl number $\mathit{Pr}= 4. 38$ . J. Fluid Mech. 676, 5–40.CrossRefGoogle Scholar
Xia, K.-Q., Lam, S. & Zhou, S. Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.Google Scholar
Zhou, S.-Q. & Ahlers, G. 2006 Spatio-temporal chaos in electro-convection of a homeotropically aligned nematic liquid crystal. Phys. Rev. E 74, 046212.Google Scholar
Zocchi, G., Moses, E. & Libchaber, A. 1990 Coherent structures in turbulent convection: an experimental study. Physica A 166, 387–407.Google Scholar