Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rahimi, Behnam
and
Struchtrup, Henning
2016.
Heat transfer in polyatomic gases.
Vol. 1786,
Issue. ,
p.
070006.
Bisi, M.
and
Spiga, G.
2017.
Hydrodynamic limits of kinetic equations for polyatomic and reactive gases.
Communications in Applied and Industrial Mathematics,
Vol. 8,
Issue. 1,
p.
23.
Gatignol, Renée
and
Croizet, Cédric
2017.
Asymptotic modeling of thermal binary monatomic gas flows in plane microchannels—Comparison with DSMC simulations.
Physics of Fluids,
Vol. 29,
Issue. 4,
Tantos, Christos
and
Valougeorgis, Dimitris
2018.
Conductive heat transfer in rarefied binary gas mixtures confined between parallel plates based on kinetic modeling.
International Journal of Heat and Mass Transfer,
Vol. 117,
Issue. ,
p.
846.
Hattori, Masanari
Kosuge, Shingo
and
Aoki, Kazuo
2018.
Slip boundary conditions for the compressible Navier-Stokes equations for a polyatomic gas.
Physical Review Fluids,
Vol. 3,
Issue. 6,
Roohi, Ehsan
Shahabi, Vahid
and
Bagherzadeh, Amir
2018.
On the vortical characteristics and cold-to-hot transfer of rarefied gas flow in a lid driven isosceles orthogonal triangular cavity with isothermal walls.
International Journal of Thermal Sciences,
Vol. 125,
Issue. ,
p.
381.
Wonnell, Louis B.
and
Chen, James
2019.
First-order approximation to the Boltzmann–Curtiss equation for flows with local spin.
Journal of Engineering Mathematics,
Vol. 114,
Issue. 1,
p.
43.
Kosuge, Shingo
Kuo, Hung-Wen
and
Aoki, Kazuo
2019.
A Kinetic Model for a Polyatomic Gas with Temperature-Dependent Specific Heats and Its Application to Shock-Wave Structure.
Journal of Statistical Physics,
Vol. 177,
Issue. 2,
p.
209.
Mankodi, Tapan K.
and
Myong, R. S.
2020.
Boltzmann-based second-order constitutive models of diatomic and polyatomic gases including the vibrational mode.
Physics of Fluids,
Vol. 32,
Issue. 12,
Oblapenko, G.
and
Kustova, E.V.
2020.
Influence of angular momentum on transport coefficients in rarefied gases.
Physica A: Statistical Mechanics and its Applications,
Vol. 553,
Issue. ,
p.
124673.
Baranger, C.
Dauvois, Y.
Marois, G.
Mathé, J.
Mathiaud, J.
and
Mieussens, L.
2020.
A BGK model for high temperature rarefied gas flows.
European Journal of Mechanics - B/Fluids,
Vol. 80,
Issue. ,
p.
1.
Alekseenko, Alexander
Grandilli, Amy
and
Wood, Aihua
2020.
An ultra-sparse approximation of kinetic solutions to spatially homogeneous flows of non-continuum gas.
Results in Applied Mathematics,
Vol. 5,
Issue. ,
p.
100085.
Aoki, Kazuo
Bisi, Marzia
Groppi, Maria
and
Kosuge, Shingo
2020.
Two-temperature Navier-Stokes equations for a polyatomic gas derived from kinetic theory.
Physical Review E,
Vol. 102,
Issue. 2,
Djordjić, Vladimir
Pavić-Čolić, Milana
and
Torrilhon, Manuel
2021.
Consistent, explicit, and accessible Boltzmann collision operator for polyatomic gases.
Physical Review E,
Vol. 104,
Issue. 2,
Kosuge, Shingo
Aoki, Kazuo
Bisi, Marzia
Groppi, Maria
and
Martalò, Giorgio
2021.
Boundary conditions for two-temperature Navier-Stokes equations for a polyatomic gas.
Physical Review Fluids,
Vol. 6,
Issue. 8,
Kosyanchuk, Vasily
and
Yakunchikov, Artem
2021.
A detailed multiscale study of rotational–translational relaxation process of diatomic molecules.
Physics of Fluids,
Vol. 33,
Issue. 2,
Aoki, Kazuo
Bisi, Marzia
Groppi, Maria
and
Kosuge, Shingo
2021.
A Note on the Steady Navier–Stokes Equations Derived from an ES–BGK Model for a Polyatomic Gas.
Fluids,
Vol. 6,
Issue. 1,
p.
32.
Djordjić, Vladimir
Pavić-Čolić, Milana
and
Spasojević, Nikola
2021.
Polytropic gas modelling at kinetic and macroscopic levels.
Kinetic & Related Models,
Vol. 14,
Issue. 3,
p.
483.
Pavić-Čolić, Milana
and
Simić, Srboljub
2022.
Kinetic description of polyatomic gases with temperature-dependent specific heats.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Kosyanchuk, Vasily
2022.
Effect of internal degrees of freedom in rarefied gas problems: Plane Couette flow.
International Journal of Heat and Mass Transfer,
Vol. 190,
Issue. ,
p.
122759.
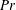 $Pr$) number. Also, the model has a proven linear H-theorem. The order of magnitude method is applied to the primary moment equations to acquire the optimized moment definitions and the final scaled set of Grad’s 36 moment equations for polyatomic gases. At the first order, a modification of the Navier–Stokes–Fourier (NSF) equations is obtained. At third order of accuracy, a set of 19 regularized partial differential equations (R19) is obtained. Furthermore, the terms associated with the internal degrees of freedom yield various intermediate orders of accuracy, a total of 13 different orders. Thereafter, boundary conditions for the proposed macroscopic model are introduced. The unsteady heat conduction of a gas at rest is studied numerically and analytically as an example of a boundary value problem. The results for different gases are given and effects of Knudsen numbers, degrees of freedom, accommodation coefficients and temperature-dependent properties are investigated. For some cases, the higher-order effects are very dominant and the widely used first-order set of the NSF equations fails to accurately capture the gas behaviour and should be replaced by the proposed higher-order set of equations.
$Pr$) number. Also, the model has a proven linear H-theorem. The order of magnitude method is applied to the primary moment equations to acquire the optimized moment definitions and the final scaled set of Grad’s 36 moment equations for polyatomic gases. At the first order, a modification of the Navier–Stokes–Fourier (NSF) equations is obtained. At third order of accuracy, a set of 19 regularized partial differential equations (R19) is obtained. Furthermore, the terms associated with the internal degrees of freedom yield various intermediate orders of accuracy, a total of 13 different orders. Thereafter, boundary conditions for the proposed macroscopic model are introduced. The unsteady heat conduction of a gas at rest is studied numerically and analytically as an example of a boundary value problem. The results for different gases are given and effects of Knudsen numbers, degrees of freedom, accommodation coefficients and temperature-dependent properties are investigated. For some cases, the higher-order effects are very dominant and the widely used first-order set of the NSF equations fails to accurately capture the gas behaviour and should be replaced by the proposed higher-order set of equations.


