Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T01:50:56.989Z Has data issue: false hasContentIssue false
  • English
  • Français

The logarithmic variance of streamwise velocity and 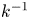$k^{-1}$ conundrum in wall turbulence

Published online by Cambridge University Press:  20 December 2021

Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window] ,
Nicholas Hutchins  and
Ivan Marusic Open the ORCID record for Ivan Marusic [Opens in a new window]
Yongyun Hwang*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

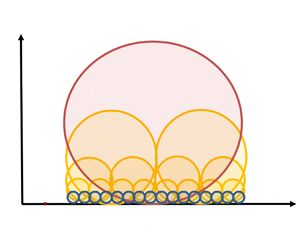
The logarithmic dependence of streamwise turbulence intensity has been observed repeatedly in recent experimental and direct numerical simulation data. However, its spectral counterpart, a well-developed $k^{-1}$ spectrum ($k$ is the spatial wavenumber in a wall-parallel direction), has not been convincingly observed from the same data. In the present study, we revisit the spectrum-based attached eddy model of Perry and co-workers, who proposed the emergence of a $k^{-1}$ spectrum in the inviscid limit, for small but finite $z/\delta$ and for finite Reynolds numbers ($z$ is the wall-normal coordinate, and $\delta$ is the outer length scale). In the upper logarithmic layer (or inertial sublayer), a reexamination reveals that the intensity of the spectrum must vary with the wall-normal location at order of $z/\delta$, consistent with the early observation argued with ‘incomplete similarity’. The streamwise turbulence intensity is subsequently calculated, demonstrating that the existence of a well-developed $k^{-1}$ spectrum is not a necessary condition for the approximate logarithmic wall-normal dependence of turbulence intensity – a more general condition is the existence of a premultiplied power-spectral intensity of $O(1)$ for $O(1/\delta ) < k < O(1/z)$. Furthermore, it is shown that the Townsend–Perry constant must be weakly dependent on the Reynolds number. Finally, the analysis is semi-empirically extended to the lower logarithmic layer (or mesolayer), and a near-wall correction for the turbulence intensity is subsequently proposed. All the predictions of the proposed model and the related analyses/assumptions are validated with high-fidelity experimental data (Samie et al., J. Fluid Mech., vol. 851, 2018, pp. 391–415).

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A8
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afzal, N. 1976 Millikan's argument at moderately large Reynolds number. Phys. Fluids 19, 600–602.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing.-Arch. 52, 355–377.CrossRefGoogle Scholar
Afzal, N. & Yajnik, K. 1973 Analysis of turbulent pipe and channel flows at moderately large Reynolds number. J. Fluid Mech. 61, 23–31.CrossRefGoogle Scholar
del Álamo, J.C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
del Álamo, J.C., Jiménez, J., Zandonade, P. & Moser, R.D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 a Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1: energy spectra. J. Fluid Mech. 882, A25.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 b Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2: integrated energy and $A_1$. J. Fluid Mech. 882, A26.CrossRefGoogle Scholar
Baars, W.J., Squire, D.T., Talluru, K.M., Abbassi, M.R., Hutchins, N. & Marusic, I. 2016 Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element. Exp. Fluids 57, 90.CrossRefGoogle Scholar
Chauhan, K.A., Monkewitz, P.A. & Nagib, H.M. 2010 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
Cheng, C., Li, W., Lozano-Durán, A. & Liu, H. 2019 Identity of attached eddies in turbulent channel flows with bidimensional empirical mode decomposition. J. Fluid Mech. 870, 1037–1071.CrossRefGoogle ScholarPubMed
Cho, M., Hwang, Y. & Choi, H. 2018 Scale interactions and spectral energy transfer in turbulent channel flow. J. Fluid Mech. 854, 474–504.CrossRefGoogle Scholar
Deshpande, R., Monty, J.P. & Marusic, I. 2020 Active and inactive components of the streamwise velocity in wall-bounded turbulence. J. Fluid Mech. 914, A5.Google Scholar
Doohan, P., Willis, A.P. & Hwang, Y. 2019 Shear stress-driven flow: the state space of near-wall turbulence as $Re_\tau \rightarrow \infty$. J. Fluid Mech. 874, 606–638.CrossRefGoogle Scholar
Eckhardt, B. & Zammert, S. 2018 Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31, R66–R77.CrossRefGoogle Scholar
Hellstöm, L.H.O., Marusic, I. & Smits, A.J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.CrossRefGoogle Scholar
Hinch, E.J. 1991 Perturbation Methods. Cambridge University Press.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S.C.C. & Smits, A.J. 2012 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flow. Phys. Rev. Fluids 1 (6), 064401.CrossRefGoogle Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010 Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluid 23, 061702.CrossRefGoogle Scholar
Hwang, Y. & Eckhardt, B.E. 2020 Attached eddy model revisited using a minimal quasilinear approximation. J. Fluid Mech. 894, A23.CrossRefGoogle Scholar
Hwang, Y. & Lee, M. 2020 The mean logarithm emerges with self-similar energy balance. J. Fluid Mech. 903, R6.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Hwang, Y., Willis, A.P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow for $Re_\tau$ up to 1000. J. Fluid Mech. 802, R1.CrossRefGoogle Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
Jiménez, J. & Moser, R.D. 2007 What are we learning from simulating wall turbulence? Phil. Trans. R. Soc. A 365, 715–732.CrossRefGoogle ScholarPubMed
Klewicki, J.C. 2013 Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.CrossRefGoogle Scholar
Lee, M.K. & Moser, R.D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_{\tau}= 5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G.J. 2003 Streamwise turbulent intensity formulation for flat-flate boundary layers. Phys. Fluids 15 (8), 2461.CrossRefGoogle Scholar
Marusic, I. & Monty, J.P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
Marusic, I., Monty, J.P., Hultmark, M. & Smits, A.J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boudnary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
McKeon, B.J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.CrossRefGoogle Scholar
McKeon, B.J. 2019 Self-similar hierarchies and attached eddies. Phys. Rev. Fluids 4, 082601(R).CrossRefGoogle Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.CrossRefGoogle Scholar
Moarref, R., Sharma, A.S., Tropp, J.A. & McKeon, B.J. 2013 Model-based scaling of the streamwise energy density in high-Reynolds-number turbulent channels. J. Fluid Mech. 734, 275–316.CrossRefGoogle Scholar
Morrison, J.F., Jiang, W., McKeon, B.J. & Smits, A.J. 2001 Reynolds number dependence of streamwise velocity spectra in turbulent pipe flow. Phys. Rev. Lett. 88 (21), 214501.CrossRefGoogle Scholar
Morrison, J.F., McKeon, B.J., Jiang, W. & Smits, A.J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.CrossRefGoogle Scholar
Nickels, T.B., Marusic, I., Hafez, S. & Chong, M.S 2005 Evidence of the $k-1$ law in a high Reynolds number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.CrossRefGoogle Scholar
Perry, A.E. & Abel, J.C. 1977 Asymptotic similarity of turbulence structures in smooth- and rough-walled pipes. J. Fluid Mech. 79, 785–799.CrossRefGoogle Scholar
Perry, A.E. & Chong, M.S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A.E., Henbest, S. & Chong, M.S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Rosenberg, B.J., Hultmark, M., Vallikivi, M., Bailey, S.C.C. & Smits, A.J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numberss. J. Fluid Mech. 731, 46–63.CrossRefGoogle Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M.K., Fan, Y., Hultmark, M. & Smits, A.J. 2018 Fully resolved measurements of turbulent boundary layer flows up to $Re_{\tau }=20\,000$. J. Fluid Mech. 851, 391–415.CrossRefGoogle Scholar
Skouloudis, N. & Hwang, Y. 2021 Scaling of turbulence intensities up to $Re_\tau =10^6$ with a resolvent-based quasilinear approximation. Phys. Rev. Fluids 6, 03460.CrossRefGoogle Scholar
Sreenivasan, K.R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. R. Panton), pp. 253–272. Comp. Mech. Publ.Google Scholar
Srinath, S., Vassilicos, J.C., Cuvier, C., Laval, J.P., Stanislas, M. & Foucaut, J.M. 2018 Attached flow structure and streamwise energy spectra in a turbulent boundary layer. Phys. Rev. E 97, 053103.CrossRefGoogle Scholar
Townsend, A.A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vadarevu, S.B., Symon, S., Illingworth, S.J. & Marusic, I. 2019 Coherent structures in the linearized impulse response of turbulent channel flow. J. Fluid Mech. 863, 1190–1203.CrossRefGoogle Scholar
Vallikivi, M., Hultmark, M. & Smits, A.J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.CrossRefGoogle Scholar
Vallikivi, M. & Smits, A.J. 2014 Fabrication and characterization of a novel nanoscale thermal anemometry probe. J. Microelectromech. Syst. 23, 899–907.CrossRefGoogle Scholar
Vassilicos, J.C., Laval, J.P., Foucaut, J.M. & Stanislas, M. 2015 The streamwise turbulence intensity in the intermediate layer of turbulent pipe flow. J. Fluid Mech. 774, 324–341.CrossRefGoogle Scholar
von Kármán, T. 1930 Mechanische aehnlichkeit und turbulenz. Nachr. Ges. Wiss. Göttingen, Math. Phys. KL., 58–68, english translation NACA TM 611.Google Scholar
Wei, T., Fife, P., Klewicki, J.C. & Mcmurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Woodcock, J.D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27, 015104.CrossRefGoogle Scholar
Yang, Q., Willis, A.P. & Hwang, Y. 2019 Exact coherent states of attached eddies in channel flow. J. Fluid Mech. 862, 1029–1059.CrossRefGoogle Scholar