Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-10T00:01:03.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct

Published online by Cambridge University Press:  10 August 2012

Jānis Priede ,
Svetlana Aleksandrova  and
Sergei Molokov
Jānis Priede*
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV1 5FB, UK
Svetlana Aleksandrova
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV1 5FB, UK
Sergei Molokov
Affiliation:
Applied Mathematics Research Centre, Coventry University, Priory Street, Coventry CV1 5FB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse numerically the linear stability of a liquid-metal flow in a rectangular duct with perfectly electrically conducting walls subject to a uniform transverse magnetic field. A non-standard three-dimensional vector stream-function/vorticity formulation is used with a Chebyshev collocation method to solve the eigenvalue problem for small-amplitude perturbations. 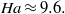A relatively weak magnetic field is found to render the flow linearly unstable as two weak jets appear close to the centre of the duct at the Hartmann number In a sufficiently strong magnetic field, the instability following the jets becomes confined in the layers of characteristic thickness 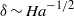located at the walls parallel to the magnetic field. In this case the instability is determined by 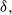which results in both the critical Reynolds number and wavenumber scaling as 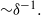Instability modes can have one of the four different symmetry combinations along and across the magnetic field. The most unstable is a pair of modes with an even distribution of vorticity along the magnetic field. These two modes represent strongly non-uniform vortices aligned with the magnetic field, which rotate either in the same or opposite senses across the magnetic field. The former enhance while the latter weaken one another provided that the magnetic field is not too strong or the walls parallel to the field are not too far apart. In a strong magnetic field, when the vortices at the opposite walls are well separated by the core flow, the critical Reynolds number and wavenumber for both of these instability modes are the same: 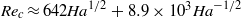and 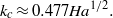The other pair of modes, which differs from the previous one by an odd distribution of vorticity along the magnetic field, is more stable with an approximately four times higher critical Reynolds number.

JFM classification

Boundary Layers: Boundary layer stability MHD and Electrohydrodynamics: High-Hartmann-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 708 , 10 October 2012 , pp. 111 - 127
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Braginskii, S. I. 1960 Magnetohydrodynamics of weakly conducting liquids. Sov. Phys. JETP 107, 1005–1014.Google Scholar
2. Branover, G. G. & Gelfgat, Y. M. 1968 Experimental study of velocity distribution for flow of a conducting fluid in rectangular ducts in a transverse magnetic field. Fluid Dyn. 1, 52–55.Google Scholar
3. Brouillette, E. C. & Lykoudis, P. S. 1967 Magneto-fluid-mechanic channel flow. I. Experiment. Phys. Fluids 10, 995–1001.CrossRefGoogle Scholar
4. Bühler, L. 2007 Liquid metal magnetohydrodynamics for fusion blankets. In Magnetohydrodynamics: Historical Evolution and Trends (ed. Molokov, S., Moreau, R. & Moffatt, H. K. ), pp. 171–194. Springer.CrossRefGoogle Scholar
5. Burr, U., Barleon, L., Müller, U. & Tsinober, A. 2000 Turbulent transport of momentum and heat in magnetohydrodynamic rectangular duct flow with strong sidewall jets. J. Fluid Mech. 406, 247–279.CrossRefGoogle Scholar
6. Chang, C. C. & Lundgren, T. S. 1961 Duct flow in magnetohydrodynamics. Z. Angew. Math. Phys. 12, 100–114.CrossRefGoogle Scholar
7. Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability (§ 31.6). Cambridge University Press.Google Scholar
8. Hocking, L. M. 1975 Non-linear stability of the asymptotic suction velocity profile. Q. J. Mech. Appl. Maths 28, 341–353.CrossRefGoogle Scholar
9. Hunt, J. C. R. 1965 Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 21, 577–590.CrossRefGoogle Scholar
10. Jackson, J. D. 1998 Classical Electrodynamics (§ 6.3). Wiley.Google Scholar
11. Kakutani, T. 1964 The hydrodynamic stability of the modified plane Couette flow in the presence of a transverse magnetic field. J. Phys. Soc. Japan 19, 1041–1057.CrossRefGoogle Scholar
12. Kinet, M., Knaepen, B. & Molokov, S. 2009 Instabilities and transition in magnetohydrodynamic flows in ducts with electrically conducting walls. Phys. Rev. Lett. 103, 154501.CrossRefGoogle ScholarPubMed
13. Lifshits, A. M. & Shtern, V. N. 1979 Monoharmonic analysis of the nonlinear stability of Hartmann flow. Magnetohydrodynamics 15, 243–248.Google Scholar
14. Lock, R. C. 1955 The stability of the flow of an electrically conducting fluid between parallel planes under a transverse magnetic field. Proc. R. Soc. Lond. A 233, 105–125.Google Scholar
15. Moresco, P. & Alboussière, T. 2003 Weakly nonlinear stability of Hartmann boundary layers. Eur. J. Mech. B Fluids 22, 345–353.CrossRefGoogle Scholar
16. Moresco, P. & Alboussière, T. 2004 Experimental study of the instability of the Hartmann layer. J. Fluid Mech. 504, 167–181.CrossRefGoogle Scholar
17. Müller, U. & Bühler, L. 2001 Magnetohydrodynamics in Channels and Containers. Springer.CrossRefGoogle Scholar
18. Murgatroyd, W. 1953 Experiments in magnetohydrodynamic channel flow. Phil. Mag. 44, 1348–1354.CrossRefGoogle Scholar
19. Pothérat, A. 2007 Quasi two-dimensional perturbations in duct flows with a transverse magnetic field. Phys. Fluids 19, 74104.CrossRefGoogle Scholar
20. Priede, J., Aleksandrova, S. & Molokov, S. 2010 Linear stability of Hunt’s flow. J. Fluid Mech. 649, 115–134.CrossRefGoogle Scholar
21. Priede, J. & Gerbeth, G. 1997 Convective, absolute and global instabilities of thermocapillary–buoyancy convection in extended layers. Phys. Rev. E 56, 4187–4199.CrossRefGoogle Scholar
22. Reed, C. B. & Picologlou, B. F. 1989 Side wall flow instabilities in liquid metal MHD flows under blanket relevant conditions. Fusion Technol. 15, 705–715.CrossRefGoogle Scholar
23. Roberts, P. H. 1967 An Introduction to Magnetohydrodynamics (§ 2.1). Longmans.Google Scholar
24. Shatrov, V. & Gerbeth, G. 2010 Marginal turbulent magnetohydrodynamic flow in a square duct. Phys. Fluids 22, 084101–9.CrossRefGoogle Scholar
25. Shercliff, J. A. 1953 Steady motion of conducting fluids in pipes under transverse magnetic fields. Proc. Camb. Phil. Soc. 49, 136–144.CrossRefGoogle Scholar
26. Tatsumi, T. & Yoshimura, T. 1990 Stability of the laminar flow in a rectangular duct. J. Fluid Mech. 212, 437–449.CrossRefGoogle Scholar
27. Ting, A. L., Walker, J. S., Moon, T. J., Reed, C. B. & Picologlou, B. F. 1991 Linear stability analysis for high-velocity boundary layers in liquid–metal magnetohydrodynamic flows. Intl J. Engng Sci. 29, 939–948.CrossRefGoogle Scholar
28. Uflyand, Ya. S. 1961 Flow stability of a conducting fluid in a rectangular channel in a transverse magnetic field. Sov. Phys.: Tech. Phys. 30, 1191–1193.Google Scholar
29. Uhlmann, M. & Nagata, M. 2006 Linear stability of flow in an internally heated rectangular duct. J. Fluid Mech. 551, 387–404.CrossRefGoogle Scholar
30. Walker, J. S. 1981 Magnetohydrodynamic flows in rectangular ducts with thin conducting walls. J. Méc. 20, 79–112.Google Scholar
31. Williams, W. E 1962 Magnetohydrodynamic flow in a rectangular tube at high Hartmann numbers. J. Fluid Mech. 16, 262–268.CrossRefGoogle Scholar