Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T20:49:35.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability analysis of a shear layer induced by differential coaxial rotation within a cylindrical enclosure

Published online by Cambridge University Press:  05 December 2013

Tony Vo ,
Luca Montabone  and
Gregory J. Sheard
Tony Vo
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Luca Montabone
Affiliation:
Atmospheric, Oceanic and Planetary Physics, University of Oxford, Parks Road, Oxford OX1 3PU, UK
Gregory J. Sheard*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The generation of distinct polygonal configurations via the instability of a Stewartson shear layer is numerically investigated. The shear layer is induced using a rotating cylindrical tank with differentially forced disks located at the top and bottom boundaries. The incompressible Navier–Stokes equations are solved on a two-dimensional semi-meridional plane. Axisymmetric base flows are consistently found to reach a steady state for a wide range of flow conditions, and details of the vertical structure are revealed. An axially invariant two-dimensional flow is ascertained for small 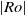$\vert \mathit{Ro}\vert $, which substantiates the Taylor–Proudman theorem. Sufficient increases in 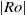$\vert \mathit{Ro}\vert $ forcing develops flow features that break this quasi-two-dimensionality. The onset of this breaking occurs earlier with increasing 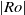$\vert \mathit{Ro}\vert $ for 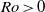$\mathit{Ro}\gt 0$ compared with 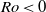$\mathit{Ro}\lt 0$. The thickness scaling of the vertical Stewartson layers are in agreement with previous analytical results. Growth rates of the most unstable azimuthal wavenumber from a global linear stability analysis are obtained. The threshold between axisymmetric and non-axisymmetric flow follows a power law, and both positive- and negative-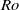$\mathit{Ro}$ regimes are found to adopt the same threshold for instability, namely 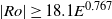$\vert \mathit{Ro}\vert \geq 18. 1{E}^{0. 767} $. This relationship corresponds to a constant critical internal Reynolds number of 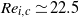${\mathit{Re}}_{i, c} \simeq 22. 5$. A review of reported critical internal Reynolds number and their characteristic length scales yields a consistent instability onset given by 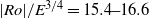$\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 4{\unicode{x2013}} 16. 6$; here we find 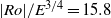$\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 8$. At the onset of linear instability, the initially circular shear layer deforms, resulting in a polygonal structure consistent with barotropic instability. Dominant azimuthal wavenumbers range from 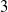$3$ to 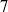$7$ at the onset of instability for the parameter space explored. Empirical relationships for the preferential wavenumber have been obtained. Additional instability modes have been discovered that favour higher wavenumbers, and these exhibit structures localized to the disk–tank interfaces.

JFM classification

Instability: Instability Geophysical and Geological Flows: Rotating flows Wakes/Jets: Shear layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 299 - 334
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Space Science Institute, Boulder, CO 80301, USA.

References

Aguiar, A. C. B. 2008 Instabilities of a shear layer in a barotropic rotating fluid. PhD thesis, University of Oxford, UK.Google Scholar
Aguiar, A. C. B. & Read, P. 2006 Instabilities of a barotropic shear layer in a rotating fluid: asymmetries with respect to $\mathrm{sgn} (Ro)$ . Meteorol. Z. 15 (4), 417–422.Google Scholar
Aguiar, A. C. B., Read, P. L., Wordsworth, R. D., Salter, T. & Yamazaki, Y. H. 2010 A laboratory model of Saturn’s north polar hexagon. Icarus 206 (2), 755–763.CrossRefGoogle Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108 (12), 124501.CrossRefGoogle ScholarPubMed
Baker, D. J. 1967 Shear layers in a rotating fluid. J. Fluid Mech. 29 (1), 165–175.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bergeron, K., Coutsias, E. A., Lynov, J. P. & Nielsen, A. H. 2000 Dynamical properties of forced shear layers in an annular geometry. J. Fluid Mech. 402 (1), 255–289.CrossRefGoogle Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.CrossRefGoogle Scholar
Blackburn, H. M. & Sheard, G. J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22, 031701.CrossRefGoogle Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Busse, F. H. 1968 Shear flow instabilities in rotating systems. J. Fluid Mech. 33 (3), 577–589.Google Scholar
Chomaz, J. M., Rabaud, M., Basdevant, C. & Couder, Y. 1988 Experimental and numerical investigation of a forced circular shear layer. J. Fluid Mech. 187, 115–140.Google Scholar
Cogan, S. J., Ryan, K. & Sheard, G. J. 2011 Symmetry breaking and instability mechanisms in medium depth torsionally driven open cylinder flows. J. Fluid Mech. 672, 521–544.CrossRefGoogle Scholar
Dyudina, U. A., Ingersoll, A. P., Ewald, S. P., Vasavada, A. R., West, R. A., Baines, K. H., Momary, T. W., Del Genio, A. D., Barbara, J. M., Porco, C. C., Achterberg, R. K., Flasar, F. M., Simon-Miller, A. A. & Fletcher, L. N. 2009 Saturn’s south polar vortex compared to other large vortices in the solar system. Icarus 202 (1), 240–248.Google Scholar
Fletcher, L. N., Irwin, P. G. J., Orton, G. S., Teanby, N. A., Achterberg, R. K., Bjoraker, G. L., Read, P. L., Simon-Miller, A. A., Howett, C., de Kok, R., Bowles, N., Calcutt, S. B., Hesman, B. & Flasar, F. M. 2008 Temperature and composition of Saturn’s polar hot spots and hexagon. Science 319 (5859), 79–81.CrossRefGoogle ScholarPubMed
Früh, W. G. & Nielsen, A. H. 2003 On the origin of time-dependent behaviour in a barotropically unstable shear layer. Nonlinear Process. Geophys. 10 (3), 289–302.Google Scholar
Früh, W. G. & Read, P. L. 1999 Experiments on a barotropic rotating shear layer. Part 1. Instability and steady vortices. J. Fluid Mech. 383, 143–173.Google Scholar
Gilman, P. A. & Fox, P. A. 1997 Joint instability of latitudinal differential rotation and toroidal magnetic fields below the solar convection zone. Astrophys. J. 484 (1), 439–454.Google Scholar
Godfrey, D. A. 1988 A hexagonal feature around Saturn’s north pole. Icarus 76, 335–356.Google Scholar
Hide, R. & Titman, C. W. 1967 Detached shear layers in a rotating fluid. J. Fluid Mech. 29 (1), 39–60.CrossRefGoogle Scholar
Hollerbach, R. 2003 Instabilities of the Stewartson layer. Part 1. The dependence on the sign of $Ro$ . J. Fluid Mech. 492, 289–302.CrossRefGoogle Scholar
Hollerbach, R. & Fournier, A. 2004 End-effects in rapidly rotating cylindrical Taylor–Couette flow. In MHD Couette Flows: Experiments and Models (ed. Rosner, R., Rüdiger, G. & Bonanno, A.), AIP Conference Proceedings, vol. 733, pp. 114–121.Google Scholar
Jansson, T. R. N., Haspang, M. P., Jensen, K. H., Hersen, P. & Bohr, T. 2006 Polygons on a rotating fluid surface. Phys. Rev. Lett. 96, 174502.Google Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444 (7117), 343–346.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
van de Konijnenberg, J. A., Nielsen, A. H., Juul Rasmussen, J. & Stenum, B. 1999 Shear-flow instability in a rotating fluid. J. Fluid Mech. 387, 177–204.Google Scholar
Kossin, J. P. & Schubert, W. H. 2001 Mesovortices, polygonal flow patterns, and rapid pressure falls in hurricane-like vortices. J. Atmos. Sci. 58, 2196–2209.2.0.CO;2>CrossRefGoogle Scholar
Kossin, J. P. & Schubert, W. H. 2004 Mesovortices in hurricane Isabel. Bull. Am. Meteorol. Soc. 85 (2), 151–153.CrossRefGoogle Scholar
Kuo, H. 1949 Dynamic instability of two-dimensional nondivergent flow in a barotropic atmosphere. J. Atmos. Sci. 6, 105–122.Google Scholar
Limaye, S. S., Kossin, J. P., Rozoff, C., Piccioni, G., Titov, D. V. & Markiewicz, W. J. 2009 Vortex circulation on Venus: dynamical similarities with terrestrial hurricanes. Geophys. Res. Lett. 36, L04204.Google Scholar
Luz, D., Berry, D. L., Piccioni, G., Drossart, P., Politi, R., Wilson, C. F., Erard, S. & Nuccilli, F. 2011 Venus’s southern polar vortex reveals precessing circulation. Science 332 (6029), 577–580.Google Scholar
Montabone, L., Wordsworth, R., Aguiar, A., Jacoby, T., Read, P. L., McClimans, T. & Ellingsen, I. 2010a Barotropic instability of planetary polar vortices: concept, experimental set-up and parameter space analysis. In Proceedings of the HYDRALAB III Joint Transnational Access User Meeting, Hannover, February 2010, pp. 135–138.Google Scholar
Montabone, L., Wordsworth, R., Aguiar, A. C. B., Jacoby, T., Manfrin, M., Read, P. L., Castrejon-Pita, A., Gostiaux, L., Sommeria, J., Viboud, S. & Didelle, H. 2010b Barotropic instability of planetary polar vortices: CIV analysis of specific multi-lobed structures. In Proceedings of the HYDRALAB III Joint Transnational Access User Meeting, Hannover, February 2010, pp. 191–194.Google Scholar
Murray, B. C., Wildey, R. L. & Westphal, J. A. 1963 Infrared photometric mapping of Venus through the 8- to 14-micron atmospheric window. J. Geophys. Res. 68, 4813–4818.Google Scholar
Niino, H. & Misawa, N. 1984 An experimental and theoretical study of barotropic instability. J. Atmos. Sci. 41 (12), 1992–2011.2.0.CO;2>CrossRefGoogle Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547, A64.CrossRefGoogle Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.CrossRefGoogle ScholarPubMed
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Peralta, C., Melatos, A., Giacobello, M. & Ooi, A. 2009 Superfluid spherical Couette flow. J. Phys.: Conf. Ser. 150, 032081.Google Scholar
Piccioni, G., Drossart, P., Sanchez-Lavega, A., Hueso, R., Taylor, F. W., Wilson, C. F., Grassi, D., Zasova, L., Moriconi, M. & Adriani, A. et al. 2007 South-polar features on Venus similar to those near the north pole. Nature 450 (7170), 637–640.CrossRefGoogle ScholarPubMed
Rayleigh, Lord 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–72.Google Scholar
Schaeffer, N. & Cardin, P. 2005 Quasigeostrophic model of the instabilities of the Stewartson layer in flat and depth-varying containers. Phys. Fluids 17, 104111.Google Scholar
Schartman, E., Ji, H., Burin, M. J. & Goodman, J. 2012 Stability of quasi-Keplerian shear flow in a laboratory experiment. Astron. Astrophys. 543, A94.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Sheard, G. J. 2009 Flow dynamics and wall shear-stress variation in a fusiform aneurysm. J. Engng Maths 64 (4), 379–390.CrossRefGoogle Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27, 734–742.Google Scholar
Sheard, G. J. & Ryan, K. 2007 Pressure-driven flow past spheres moving in a circular tube. J. Fluid Mech. 592, 233–262.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005 Subharmonic mechanism of the mode C instability. Phys. Fluids 17, 111702.CrossRefGoogle Scholar
Smith, S. H. 1984 The development of nonlinearities in the ${E}^{1/ 3} $ Stewartson layer. Q. J. Mech. Appl. Math. 37 (1), 75–85.Google Scholar
Solomon, T. H., Holloway, W. J. & Swinney, H. L. 1993 Shear flow instabilities and Rossby waves in barotropic flow in a rotating annulus. Phys. Fluids A: Fluid Dyn. 5, 1971–1971.Google Scholar
Sommeria, J., Meyers, S. D. & Swinney, H. L. 1991 Experiments on vortices and Rossby waves in eastward and westward jets. Nonlinear Topics Ocean Phys. 109, 227–269.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.CrossRefGoogle Scholar
Taylor, F. W., Diner, D. J., Elson, L. S., McCleese, D. J., Martonchik, J. V., Delderfield, J., Bradley, S. P., Schofield, J. T., Gille, J. C. & Coffey, M. T. 1979 Temperature, cloud structure, and dynamics of Venus middle atmosphere by infrared remote sensing from Pioneer Orbiter. Science 205 (4401), 65–67.CrossRefGoogle ScholarPubMed
Vatistas, G. H. 1990 A note on liquid vortex sloshing and Kelvin’s equilibria. J. Fluid Mech. 217 (1), 241–248.Google Scholar
Vo, T., Sheard, G. J. & Montabone, L. 2011 Stability of a rotating tank source–sink setup to model a polar vortex. In Mechanical, Industrial, and Manufacturing Engineering (ed. Ma, M.), pp. 251–254. Information Engineering Research Institute.Google Scholar
Vooren, A. I. 1992 The Stewartson layer of a rotating disk of finite radius. J. Engng Math. 26 (1), 131–152.Google Scholar