Article contents
Linear modal instabilities of hypersonic flow over an elliptic cone
Published online by Cambridge University Press: 09 September 2016
Abstract
Steady laminar flow over a rounded-tip 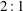 $2\,:\,1$ elliptic cone of 0.86 m length at zero angle of attack and yaw has been computed at Mach number
$2\,:\,1$ elliptic cone of 0.86 m length at zero angle of attack and yaw has been computed at Mach number 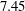 $7.45$ and unit Reynolds number
$7.45$ and unit Reynolds number 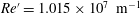 $Re^{\prime }=1.015\times 10^{7}~\text{m}^{-1}$. The flow conditions are selected to match the planned flight of the Hypersonic Flight Research Experimentation HIFiRE-5 test geometry at an altitude of 21.8 km. Spatial linear BiGlobal modal instability analysis of this flow has been performed at selected streamwise locations on planes normal to the cone symmetry axis, resolving the entire flow domain in a coupled manner while exploiting flow symmetries. Four amplified classes of linear eigenmodes have been unravelled. The shear layer formed near the cone minor-axis centreline gives rise to amplified symmetric and antisymmetric centreline instability modes, classified as shear-layer instabilities. At the attachment line formed along the major axis of the cone, both symmetric and antisymmetric instabilities are also discovered and identified as boundary-layer second Mack modes. In both cases of centreline and attachment-line modes, symmetric instabilities are found to be more unstable than their antisymmetric counterparts. Furthermore, spatial BiGlobal analysis is used for the first time to resolve oblique second modes and cross-flow instabilities in the boundary layer between the major- and minor-axis meridians. Contrary to predictions for the incompressible regime for swept infinite wing flow, the cross-flow instabilities are not found to be linked to the attachment-line instabilities. In fact, cross-flow modes peak along most of the surface of the cone, but vanish towards the attachment line. On the other hand, the leading oblique second modes peak near the leading edge and their associated frequencies are in the range of the attachment-line instability frequencies. Consequently, the attachment-line instabilities are observed to be related to oblique second modes at the major-axis meridian. The linear amplification of centreline and attachment-line instability modes is found to be strong enough to lead to laminar–turbulent flow transition within the length of the test object. The predictions of global linear theory are compared with those of local instability analysis, also performed here under the assumption of locally parallel flow, where use of this assumption is permissible. Fair agreement is obtained for symmetric centreline and symmetric attachment-line modes, while for all other classes of linear disturbances use of the proposed global analysis methodology is warranted for accurate linear instability predictions.
$Re^{\prime }=1.015\times 10^{7}~\text{m}^{-1}$. The flow conditions are selected to match the planned flight of the Hypersonic Flight Research Experimentation HIFiRE-5 test geometry at an altitude of 21.8 km. Spatial linear BiGlobal modal instability analysis of this flow has been performed at selected streamwise locations on planes normal to the cone symmetry axis, resolving the entire flow domain in a coupled manner while exploiting flow symmetries. Four amplified classes of linear eigenmodes have been unravelled. The shear layer formed near the cone minor-axis centreline gives rise to amplified symmetric and antisymmetric centreline instability modes, classified as shear-layer instabilities. At the attachment line formed along the major axis of the cone, both symmetric and antisymmetric instabilities are also discovered and identified as boundary-layer second Mack modes. In both cases of centreline and attachment-line modes, symmetric instabilities are found to be more unstable than their antisymmetric counterparts. Furthermore, spatial BiGlobal analysis is used for the first time to resolve oblique second modes and cross-flow instabilities in the boundary layer between the major- and minor-axis meridians. Contrary to predictions for the incompressible regime for swept infinite wing flow, the cross-flow instabilities are not found to be linked to the attachment-line instabilities. In fact, cross-flow modes peak along most of the surface of the cone, but vanish towards the attachment line. On the other hand, the leading oblique second modes peak near the leading edge and their associated frequencies are in the range of the attachment-line instability frequencies. Consequently, the attachment-line instabilities are observed to be related to oblique second modes at the major-axis meridian. The linear amplification of centreline and attachment-line instability modes is found to be strong enough to lead to laminar–turbulent flow transition within the length of the test object. The predictions of global linear theory are compared with those of local instability analysis, also performed here under the assumption of locally parallel flow, where use of this assumption is permissible. Fair agreement is obtained for symmetric centreline and symmetric attachment-line modes, while for all other classes of linear disturbances use of the proposed global analysis methodology is warranted for accurate linear instability predictions.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 57
- Cited by



